Refine listing
Actions for selected content:
355 results in 14Gxx
Automorphisms of Drinfeld half-spaces over a finite field
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 26 April 2013, pp. 1211-1224
- Print publication:
- July 2013
-
- Article
- Export citation
The André–Oort conjecture for Drinfeld modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 507-567
- Print publication:
- April 2013
-
- Article
- Export citation
Random Dieudonné modules, random
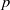 $p$-divisible groups, and random curves over finite fields
$p$-divisible groups, and random curves over finite fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 13 February 2013, pp. 651-676
- Print publication:
- July 2013
-
- Article
- Export citation
Failure of the Hasse principle on general
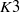 $K 3$ surfaces
$K 3$ surfaces
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 08 February 2013, pp. 853-877
- Print publication:
- October 2013
-
- Article
- Export citation
ON A CONJECTURE OF IGUSA
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 399-425
- Print publication:
- July 2013
-
- Article
- Export citation
Seven new champion linear codes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 January 2013, pp. 109-117
-
- Article
-
- You have access
- Export citation
p-adic modular forms of non-integral weight over Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 01 November 2012, pp. 32-62
- Print publication:
- January 2013
-
- Article
- Export citation
On the center of the ring of differential operators on a smooth variety over ℤ/pnℤ
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 63-80
- Print publication:
- January 2013
-
- Article
- Export citation
ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 169-176
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
On arithmetic families of filtered
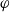 $\varphi $-modules and crystalline representations
$\varphi $-modules and crystalline representations
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 19 September 2012, pp. 677-726
- Print publication:
- October 2013
-
- Article
- Export citation
On the use of expansion series for stream ciphers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 326-340
-
- Article
-
- You have access
- Export citation
Sato–Tate distributions and Galois endomorphism modules in genus 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1390-1442
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Descent obstructions and Brauer–Manin obstruction in positive characteristic
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 01 June 2012, pp. 545-551
- Print publication:
- July 2013
-
- Article
- Export citation
Covers in p-adic analytic geometry and log covers II: cospecialization of the (p′)-tempered fundamental group in higher dimensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1443-1482
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Slopes of the U7 operator acting on a space of overconvergent modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 113-139
-
- Article
-
- You have access
- Export citation
On the equations a2−2b6=cp and a2−2=cp
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 158-171
-
- Article
-
- You have access
- Export citation
Opérateur de Lefschetz sur les tours de Drinfeld et Lubin–Tate
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 507-530
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Proving the Birch and Swinnerton-Dyer conjecture for specific elliptic curves of analytic rank zero and one
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 327-350
-
- Article
-
- You have access
- Export citation
Some unlikely intersections beyond André–Oort
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 August 2011, pp. 1-27
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Remarks on endomorphisms and rational points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 24 August 2011, pp. 1819-1842
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
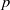
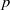
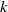
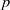
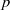

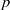
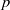
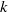
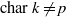
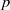
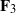
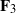
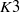
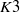
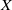
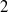

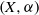

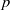
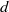
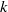

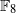
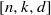
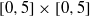
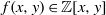
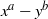
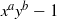
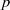
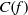
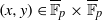
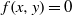
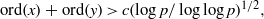

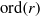

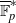
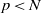
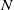
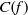
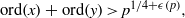
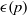
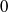
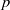
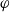
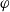
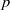
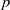
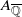 (the
(the 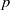
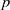
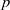
 . Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of
. Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of 