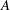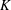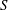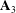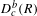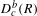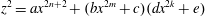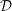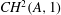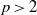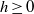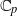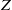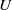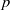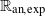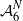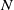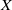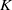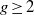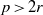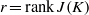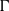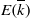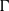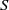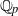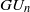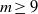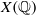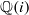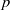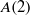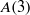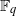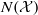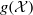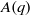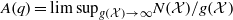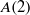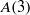Refine listing
Actions for selected content:
355 results in 14Gxx
Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 257-273
-
- Article
-
- You have access
- Export citation
Computation of Mordell–Weil bases for ordinary elliptic curves in characteristic two
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 1-13
-
- Article
-
- You have access
- Export citation
Hyper-and-elliptic-curve cryptography
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 181-202
-
- Article
-
- You have access
- Export citation
Counting imaginary quadratic points via universal torsors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 1631-1678
- Print publication:
- October 2014
-
- Article
- Export citation
RATIONAL POINTS ON INTERSECTIONS OF CUBIC AND QUADRIC HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 05 June 2014, pp. 703-749
- Print publication:
- October 2015
-
- Article
- Export citation
THE p-COHOMOLOGY OF ALGEBRAIC VARIETIES AND SPECIAL VALUES OF ZETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 02 June 2014, pp. 801-835
- Print publication:
- October 2015
-
- Article
- Export citation
FROM SEPARABLE POLYNOMIALS TO NONEXISTENCE OF RATIONAL POINTS ON CERTAIN HYPERELLIPTIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 354-385
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
SUR LES COMPOSANTES CONNEXES D’UNE FAMILLE D’ESPACES ANALYTIQUES
 ${P}$ -ADIQUES
${P}$ -ADIQUES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 29 May 2014, e14
-
- Article
-
- You have access
- Open access
- Export citation
EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 14 May 2014, pp. 257-306
- Print publication:
- July 2014
-
- Article
- Export citation
Higher Chow cycles on Abelian surfaces and a non-Archimedean analogue of the Hodge-
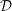 ${\mathcal{D}}$-conjecture
${\mathcal{D}}$-conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 691-711
- Print publication:
- April 2014
-
- Article
- Export citation
Overconvergent Eichler–Shimura isomorphisms
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 02 January 2014, pp. 221-274
- Print publication:
- April 2015
-
- Article
- Export citation
Applications du théorème d’Ax–Lindemann hyperbolique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 19 November 2013, pp. 175-190
- Print publication:
- February 2014
-
- Article
- Export citation
The Chabauty–Coleman bound at a prime of bad reduction and Clifford bounds for geometric rank functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 09 October 2013, pp. 1818-1838
- Print publication:
- November 2013
-
- Article
- Export citation
Integral division points on curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 09 September 2013, pp. 2011-2035
- Print publication:
- December 2013
-
- Article
- Export citation
Variants of formal nearby cycles
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 19 August 2013, pp. 701-752
- Print publication:
- October 2014
-
- Article
- Export citation
Topological flatness of local models for ramified unitary groups. II. The even dimensional case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 10 July 2013, pp. 303-393
- Print publication:
- April 2014
-
- Article
- Export citation
On the arithmetic fundamental lemma in the minuscule case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 04 July 2013, pp. 1631-1666
- Print publication:
- October 2013
-
- Article
- Export citation
Rational points on singular intersections of quadrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 20 June 2013, pp. 1457-1494
- Print publication:
- September 2013
-
- Article
- Export citation
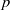 $p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES
$p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 17 May 2013, e1
-
- Article
-
- You have access
- Open access
- Export citation
On lower bounds for the Ihara constants
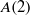 $A(2)$ and
$A(2)$ and 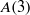 $A(3)$
$A(3)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1108-1128
- Print publication:
- July 2013
-
- Article
- Export citation