Article contents
EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
Published online by Cambridge University Press: 14 May 2014
Abstract
We study the automorphic Green function 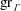 $\mathop{\rm gr}\nolimits _\Gamma $ on quotients of the hyperbolic plane by cofinite Fuchsian groups
$\mathop{\rm gr}\nolimits _\Gamma $ on quotients of the hyperbolic plane by cofinite Fuchsian groups 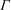 $\Gamma $, and the canonical Green function
$\Gamma $, and the canonical Green function 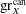 $\mathop{\rm gr}\nolimits ^{\rm can}_X$ on the standard compactification
$\mathop{\rm gr}\nolimits ^{\rm can}_X$ on the standard compactification 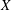 $X$ of such a quotient. We use a limiting procedure, starting from the resolvent kernel, and lattice point estimates for the action of
$X$ of such a quotient. We use a limiting procedure, starting from the resolvent kernel, and lattice point estimates for the action of 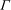 $\Gamma $ on the hyperbolic plane to prove an “approximate spectral representation” for
$\Gamma $ on the hyperbolic plane to prove an “approximate spectral representation” for 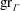 $\mathop{\rm gr}\nolimits _\Gamma $. Combining this with bounds on Maaß forms and Eisenstein series for
$\mathop{\rm gr}\nolimits _\Gamma $. Combining this with bounds on Maaß forms and Eisenstein series for 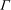 $\Gamma $, we prove explicit bounds on
$\Gamma $, we prove explicit bounds on 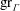 $\mathop{\rm gr}\nolimits _\Gamma $. From these results on
$\mathop{\rm gr}\nolimits _\Gamma $. From these results on 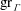 $\mathop{\rm gr}\nolimits _\Gamma $ and new explicit bounds on the canonical
$\mathop{\rm gr}\nolimits _\Gamma $ and new explicit bounds on the canonical 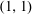 $(1,1)$-form of
$(1,1)$-form of 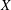 $X$, we deduce explicit bounds on
$X$, we deduce explicit bounds on 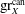 $\mathop{\rm gr}\nolimits ^{\rm can}_X$.
$\mathop{\rm gr}\nolimits ^{\rm can}_X$.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2014
References
- 4
- Cited by

