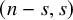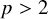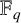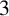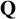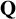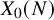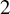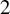Refine listing
Actions for selected content:
355 results in 14Gxx
Arithmetic Transfer for inner forms of
 $GL_{2n}$
$GL_{2n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semi-stable and splitting models for unitary Shimura varieties over ramified places. I.
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 July 2025, e119
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modularity of arithmetic special divisors for unitary Shimura varieties (with an appendix by Yujie Xu)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SINGULARITIES OF QUOTIENTS BY 1-FOLIATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Canonical integral models for Shimura varieties of abelian type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A linear AFL for quaternion algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-23
-
- Article
- Export citation
ON THE NON-ARCHIMEDEAN MONGE–AMPÈRE EQUATION IN MIXED CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kodaira–Spencer isomorphisms and degeneracy maps on Iwahori-level Hilbert modular varieties: the saving trace
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 February 2025, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR SYSTEMS OF GEOMETRICALLY IRREDUCIBLE PLANE CUBICS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 February 2025, pp. 1-9
-
- Article
- Export citation
POLYNOMIALS REPRESENTED BY NORM FORMS VIA THE BETA SIEVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1463-1519
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-adic Simpson correspondences for principal bundles in abelian settings
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Average Analytic Ranks of Elliptic Curves over Number Fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 February 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-LOG LIFTABLE LOG DEL PEZZO SURFACES OF RANK ONE IN CHARACTERISTIC FIVE
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-24
-
- Article
- Export citation
On the L-polynomials of curves over finite fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
“The six-functor formalism for rigid analytic motives” – Erratum
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 February 2025, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the linear AFL: the non-basic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 385-425
- Print publication:
- February 2025
-
- Article
- Export citation
Positivity, plethysm and hyperbolicity of Siegel varieties in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 257-304
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complete verification of strong BSD for many modular abelian surfaces over
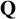 ${\mathbf {Q}}$
${\mathbf {Q}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rich representations and superrigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 2249-2272
- Print publication:
- August 2025
-
- Article
- Export citation
AN UPPER BOUND FOR THE GENERALISED GREATEST COMMON DIVISOR OF RATIONAL POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-6
-
- Article
- Export citation