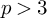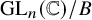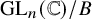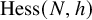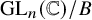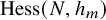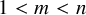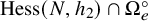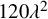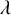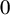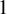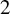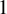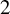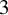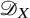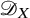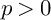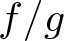Refine listing
Actions for selected content:
108 results in 14Bxx
ON THE SINGULARITIES OF QUOTIENTS BY 1-FOLIATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inversion of Adjunction for the minimal exponent
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motivic Vitushkin invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 959-992
- Print publication:
- May 2025
-
- Article
- Export citation
Limits of nodal surfaces and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERAL HYPERPLANE SECTIONS OF LOG CANONICAL THREEFOLDS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-28
-
- Article
- Export citation
Bernstein–Sato polynomials of locally quasi-homogeneous divisors in
 $\mathbb{C}^{3}$
$\mathbb{C}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 859-915
- Print publication:
- April 2025
-
- Article
- Export citation
TRIANGULATED CHARACTERIZATIONS OF SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-15
-
- Article
- Export citation
Local Normal Forms of Noncommutative Functions
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coordinate rings of regular nilpotent Hessenberg varieties in the open opposite schubert cell
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 February 2025, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complements and coregularity of Fano varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of morphisms of sheaves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 February 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semiregularity as a consequence of Goodwillie’s theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 December 2024, e126
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Atiyah class on algebraic stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 November 2024, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperplane Arrangements Satisfy (Un)Twisted Logarithmic Comparison Theorems, Applications to
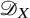 $\mathscr {D}_{X}$-modules
$\mathscr {D}_{X}$-modules
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING TORSORS UNDER QUASI-FINITE FLAT GROUP SCHEMES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 45-54
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the embedded Nash problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 16 October 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equisingularity in pencils of curves on germs of reduced complex surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 04 June 2024, pp. 990-1012
-
- Article
- Export citation
Strict positivity of Kähler–Einstein currents
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 938-952
- Print publication:
- December 2024
-
- Article
- Export citation
Convexity of multiplicities of filtrations on local rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 878-914
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation