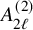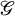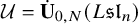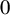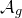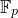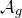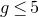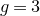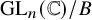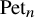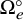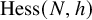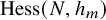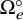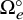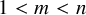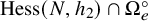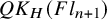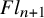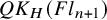Refine listing
Actions for selected content:
181 results in 14Mxx
Quantum K theory of Grassmannians, Wilson line operators and Schur bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 September 2025, e140
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regularity and multiplicity of Veronese type algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the formal Peterson subalgebra and its dual
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TORSION BIRATIONAL MOTIVES OF SURFACES AND UNRAMIFIED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-33
-
- Article
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-Orbit closures and Hessenberg varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 June 2025, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic Chow stability of symmetric reflexive toric varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Newell–Littlewood numbers III: Eigencones and GIT-semigroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1054-1074
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the irreducibility of Hessian loci of cubic hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A categorical action of the shifted
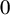 $0$-affine algebra
$0$-affine algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 April 2025, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rationality and arithmetic of the moduli of abelian varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOTT MANIFOLDS WITH VANISHING FUTAKI INVARIANTS FOR ALL KAHLER CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-20
-
- Article
- Export citation
Coordinate rings of regular nilpotent Hessenberg varieties in the open opposite schubert cell
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 February 2025, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometrization of the Satake transform for mod p Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A presentation of the torus-equivariant quantum K-theory ring of flag manifolds of type A, Part II: quantum double Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Casimir operators for loop Lie superalgebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 744-760
- Print publication:
- September 2025
-
- Article
- Export citation
Generic stabilizers for simple algebraic groups acting on orthogonal and symplectic Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 ${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION
${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 237-283
- Print publication:
- June 2025
-
- Article
- Export citation
TWO NON-VANISHING RESULTS CONCERNING THE ANTI-CANONICAL BUNDLE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 201-218
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4-Torsion classes in the integral cohomology of oriented Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 January 2025, pp. 1-43
-
- Article
- Export citation