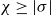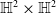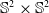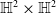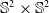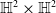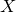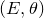Refine listing
Actions for selected content:
476 results in 53Cxx
On K-stability of blow-ups of weighted projective planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-17
-
- Article
- Export citation
Alexandrov sphere theorems for
 $ W^{2,n} $-hypersurfaces
$ W^{2,n} $-hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characteristic numbers of manifold bundles over spheres and positive curvature via block bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e138
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On G2-manifolds and geometry in dimensions 6 and 8
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-9
-
- Article
- Export citation
Conformally Kähler structures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal surfaces in the Lorentzian Heisenberg group
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 29 July 2025, pp. 1-30
-
- Article
- Export citation
LORENTZIAN BCV SPACES: PROPERTIES AND GEOMETRY OF THEIR SURFACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 25 July 2025, pp. 129-151
- Print publication:
- October 2025
-
- Article
- Export citation
Aspherical complex surfaces, the Singer conjecture, and Gromov–Lück inequality
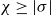 $\chi \ge |\sigma |$
$\chi \ge |\sigma |$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 17 July 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECIAL RICCI–HESSIAN EQUATIONS ON KÄHLER MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-21
-
- Article
- Export citation
Smooth orbit equivalence rigidity for dissipative geodesic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 26 May 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A strong Frankel theorem for shrinkers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 19 August 2025, pp. 947-958
- Print publication:
- May 2025
-
- Article
- Export citation
Correspondence between Pestov and Weitzenböck identities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 02 May 2025, pp. 443-463
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On hypersurfaces of
 $\mathbb{S}^2\times \mathbb{S}^2$ and
$\mathbb{S}^2\times \mathbb{S}^2$ and 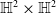 $\mathbb{H}^2\times \mathbb{H}^2$ with recurrent Ricci tensor
$\mathbb{H}^2\times \mathbb{H}^2$ with recurrent Ricci tensor
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 30 April 2025, pp. 1-21
-
- Article
- Export citation
Minimal Lagrangian submanifolds of weighted Kim–McCann metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1-16
-
- Article
- Export citation
ASYMPTOTIC DIMENSION AND GEOMETRIC DECOMPOSITIONS IN DIMENSIONS 3 AND 4
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 176-201
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviour of large-scale solutions of Hitchin’s equations in higher rank
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Codazzi and totally umbilical hypersurfaces in
 $\mathrm {Sol}_1^4$
$\mathrm {Sol}_1^4$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 April 2025, pp. 487-493
- Print publication:
- September 2025
-
- Article
- Export citation
DISTANCE FUNCTIONS ON CONVEX BODIES AND SYMPLECTIC TORIC MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-23
-
- Article
- Export citation
GAUSSIAN HOLOMORPHIC SECTIONS ON NONCOMPACT COMPLEX MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1197-1262
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPLETE HYPERSURFACES WITH LINEARLY RELATED HIGHER ORDER MEAN CURVATURES IN THE HYPERBOLIC SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 82-105
- Print publication:
- August 2025
-
- Article
- Export citation