Hostname: page-component-69cd664f8f-lpdgq Total loading time: 0 Render date: 2025-03-13T06:50:29.905Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLETE HYPERSURFACES WITH LINEARLY RELATED HIGHER ORDER MEAN CURVATURES IN THE HYPERBOLIC SPACE

Part of: Classical differential geometry Global differential geometry

Published online by Cambridge University Press:  10 March 2025

ARY V. F. LEITE Open the ORCID record for ARY V. F. LEITE [Opens in a new window] ,
HENRIQUE F. DE LIMA Open the ORCID record for HENRIQUE F. DE LIMA [Opens in a new window]  and
MARCO A. L. VELÁSQUEZ Open the ORCID record for MARCO A. L. VELÁSQUEZ [Opens in a new window]
ARY V. F. LEITE*
Affiliation:
Departamento de Matemática, Universidade Federal de Campina Grande, 58.429-970 Campina Grande, Paraíba, Brazil
HENRIQUE F. DE LIMA
Affiliation:
Departamento de Matemática, Universidade Federal de Campina Grande, 58.429-970 Campina Grande, Paraíba, Brazil e-mail: henriquedelima74@gmail.com
MARCO A. L. VELÁSQUEZ
Affiliation:
Departamento de Matemática, Universidade Federal de Campina Grande, 58.429-970 Campina Grande, Paraíba, Brazil e-mail: marcolazarovelasquez@gmail.com
*
e-mail: ary.v.l.f@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we study the behavior of complete two-sided hypersurfaces immersed in the hyperbolic space 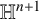$\mathbb H^{n+1}$. Initially, we introduce the concept of the linearized curvature function 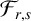$\mathcal {F}_{r,s}$ of a two-sided hypersurface, its associated modified Newton transformation 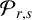$\mathcal {P}_{r,s}$ and its naturally attached differential operator 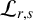$\mathcal {L}_{r,s}$. Then, we obtain two formulas for differential operator 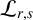$\mathcal {L}_{r,s}$ acting on the height function of a two-sided hypersurface and, for the case where their support functions are related by a negative constant, we derive two new formulas for the Newton transformation 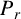$P_{r}$ and the modified Newton transformation 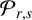$\mathcal {P}_{r,s}$ acting on a gradient of the height function. Finally, these formulas, jointly with suitable maximum principles, enable us to establish our rigidity and nonexistence results concerning complete two-sided hypersurfaces in 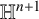$\mathbb H^{n+1}$.

Keywords

hyperbolic spacecomplete two-sided hypersurfaceshorospheresclosed horoballhigher order mean curvatures

MSC classification

Primary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Secondary: 53A10: Minimal surfaces, surfaces with prescribed mean curvature 53C20: Global Riemannian geometry, including pinching
Type
Research Article
Information
Journal of the Australian Mathematical Society , First View , pp. 1 - 24
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by James McCoy

The first author is partially supported by CAPES, Brazil. The second and third authors are partially supported by CNPq, Brazil, grants 305608/2023-1 and 304891/2021-5, respectively.

References

Alías, L. J., Caminha, A. and do Nascimento, F. Y., ‘A maximum principle related to volume growth and applications’, Ann. Mat. Pura Appl. (4) 200 (2021), 1637–1650.CrossRefGoogle Scholar
Alías, L. J., Caminha, A. and do Nascimento, F. Y. S., ‘A maximum principle at infinity with applications to geometric vector fields’, J. Math. Anal. Appl. 474 (2019), 242–247.CrossRefGoogle Scholar
Alías, L. J. and Dajczer, M., ‘Uniqueness of constant mean curvature surfaces properly immersed in a slab’, Comment. Math. Helv. 81 (2006), 653–663.CrossRefGoogle Scholar
Alías, L. J., de Lira, J. H. S. and Malacarne, J. M., ‘Constant higher-order mean curvature hypersurfaces in Riemannian spaces’, J. Inst. Math. Jussieu 5 (2006), 527–562.CrossRefGoogle Scholar
Alías, L. J., Impera, D. and Rigoli, M., ‘Spacelike hypersurfaces of constant higher order mean curvature in generalized Robertson–Walker spacetimes’, Math. Proc. Cambridge Philos. Soc. 152 (2012), 365–383.CrossRefGoogle Scholar
Alías, L. J., Mastrolia, P. and Rigoli, M., Maximum Principles and Geometric Applications (Springer Monographs in Mathematics, New York, 2016).CrossRefGoogle Scholar
Aquino, C. P., Baltazar, H. I. and de Lima, H. F., ‘Characterizing horospheres of the hyperbolic space via higher order mean curvatures’, Differential Geom. Appl. 62 (2019), 109–119.CrossRefGoogle Scholar
Caminha, A., ‘The geometry of closed conformal vector fields on Riemannian spaces’, Bull. Braz. Math. Soc. (N.S.) 42 (2011), 277–300.CrossRefGoogle Scholar
Colares, A. G., de Lima, H. F. and Velásquez, M. A. L., ‘Revisiting the geometry of horospheres of the hyperbolic space’, Monatsh. Math. 199 (2022), 771–784.CrossRefGoogle Scholar
do Carmo, M. and Lawson, B., ‘The Alexandrov–Bernstein theorems in hyperbolic space’, Duke Math. J. 50 (1983), 995–1003.CrossRefGoogle Scholar
Elbert, M. F., ‘Constant positive $2$ -mean curvature hypersurfaces’, Illinois J. Math. 46 (2002), 247–267.CrossRefGoogle Scholar
Gaffney, M., ‘A special Stokes’ theorem for complete Riemannian manifolds’, Ann. of Math. (2) 60 (1954), 140–145.CrossRefGoogle Scholar
Gårding, L., ‘An inequality for hyperbolic polynomials’, J. Math. Mech. 8 (1959), 957–965.Google Scholar
López, R. and Montiel, S., ‘Existence of constant mean curvature graphs in hyperbolic space’, Calc. Var. Partial Differential Equations 8 (1999), 177–190.Google Scholar
Montiel, S., ‘Unicity of constant mean curvature hypersurfaces in some Riemannian manifolds’, Indiana Univ. Math. J. 48 (1999), 711–748.CrossRefGoogle Scholar
Omori, H., ‘Isometric immersions of Riemannian manifolds’, J. Math. Soc. Japan 19 (1967), 205–214.CrossRefGoogle Scholar
Rosenberg, H., ‘Hypersurfaces of constant curvature in space forms’, Bull. Sci. Math. 117 (1993), 217–239.Google Scholar
Yau, S. T., ‘Harmonic functions on complete Riemannian manifolds’, Comm. Pure Appl. Math. 28 (1975), 201–228.CrossRefGoogle Scholar
Yau, S. T., ‘Some function-theoretic properties of complete Riemannian manifolds and their applications to geometry’, Indiana Univ. Math. J. 25 (1976), 659–670.CrossRefGoogle Scholar