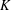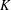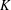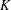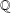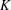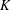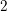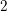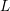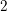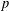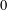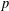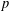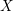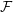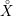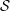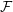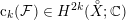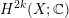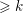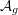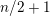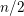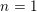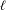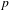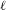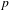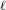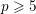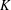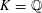Refine listing
Actions for selected content:
355 results in 14Gxx
Odd zeta motive and linear forms in odd zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 342-379
- Print publication:
- February 2018
-
- Article
- Export citation
ON PERFECT
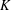 $K$ -RATIONAL CUBOIDS
$K$ -RATIONAL CUBOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 26-32
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Corrigendum: Local and global structure of connections on nonarchimedean curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2658-2665
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
Bad reduction of genus
 $2$ curves with CM jacobian varieties
$2$ curves with CM jacobian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 11 September 2017, pp. 2534-2576
- Print publication:
- December 2017
-
- Article
- Export citation
A QUOTIENT OF THE LUBIN–TATE TOWER
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 July 2017, e17
-
- Article
-
- You have access
- Open access
- Export citation
TRANSPORT PARALLÈLE ET CORRESPONDANCE DE SIMPSON
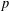 $p$ -ADIQUE
$p$ -ADIQUE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 19 June 2017, e13
-
- Article
-
- You have access
- Open access
- Export citation
Minimal weights of Hilbert modular forms in characteristic
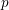 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 13 June 2017, pp. 1769-1778
- Print publication:
- September 2017
-
- Article
- Export citation
Goresky–Pardon lifts of Chern classes and associated Tate extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 1349-1371
- Print publication:
- July 2017
-
- Article
- Export citation
RATIONAL POINTS ON SHIMURA CURVES AND THE MANIN OBSTRUCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 12 April 2017, pp. 144-159
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
Rapoport–Zink spaces for spinor groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 10 April 2017, pp. 1050-1118
- Print publication:
- May 2017
-
- Article
- Export citation
Bezout-type theorems for differential fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 867-888
- Print publication:
- April 2017
-
- Article
- Export citation
Height pairings on orthogonal Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 474-534
- Print publication:
- March 2017
-
- Article
- Export citation
MANY CUBIC SURFACES CONTAIN RATIONAL POINTS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 818-839
- Print publication:
- 2017
-
- Article
- Export citation
Corrigendum: Connected components of affine Deligne–Lusztig varieties in mixed characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 218-222
- Print publication:
- January 2017
-
- Article
-
- You have access
- HTML
- Export citation
RATIONAL POINTS ON THE INNER PRODUCT CONE VIA THE HYPERBOLA METHOD
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 780-796
- Print publication:
- 2017
-
- Article
- Export citation
ON THE COHOMOLOGY OF SOME SIMPLE SHIMURA VARIETIES WITH BAD REDUCTION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 December 2016, pp. 1-24
- Print publication:
- January 2019
-
- Article
- Export citation
ON THE
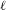 $\ell$-ADIC COHOMOLOGY OF SOME
$\ell$-ADIC COHOMOLOGY OF SOME 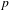 $p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
$p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 01 December 2016, pp. 1197-1226
- Print publication:
- November 2018
-
- Article
- Export citation
2-ADIC INTEGRAL CANONICAL MODELS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 05 October 2016, e28
-
- Article
-
- You have access
- Open access
- Export citation
Local models for Weil-restricted groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 27 September 2016, pp. 2563-2601
- Print publication:
- December 2016
-
- Article
- Export citation
FORMS OF DIFFERING DEGREES OVER NUMBER FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 92-123
- Print publication:
- 2017
-
- Article
- Export citation