Article contents
Goresky–Pardon lifts of Chern classes and associated Tate extensions
Published online by Cambridge University Press: 03 May 2017
Abstract
Let 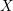 $X$ be an irreducible complex-analytic variety,
$X$ be an irreducible complex-analytic variety, 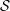 ${\mathcal{S}}$ a stratification of
${\mathcal{S}}$ a stratification of 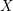 $X$ and
$X$ and 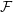 ${\mathcal{F}}$ a holomorphic vector bundle on the open stratum
${\mathcal{F}}$ a holomorphic vector bundle on the open stratum 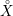 ${X\unicode[STIX]{x0030A}}$ . We give geometric conditions on
${X\unicode[STIX]{x0030A}}$ . We give geometric conditions on 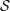 ${\mathcal{S}}$ and
${\mathcal{S}}$ and 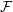 ${\mathcal{F}}$ that produce a natural lift of the Chern class
${\mathcal{F}}$ that produce a natural lift of the Chern class 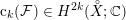 $\operatorname{c}_{k}({\mathcal{F}})\in H^{2k}({X\unicode[STIX]{x0030A}};\mathbb{C})$ to
$\operatorname{c}_{k}({\mathcal{F}})\in H^{2k}({X\unicode[STIX]{x0030A}};\mathbb{C})$ to 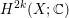 $H^{2k}(X;\mathbb{C})$ , which, in the algebraic setting, is of Hodge level
$H^{2k}(X;\mathbb{C})$ , which, in the algebraic setting, is of Hodge level 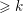 ${\geqslant}k$ . When applied to the Baily–Borel compactification
${\geqslant}k$ . When applied to the Baily–Borel compactification 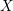 $X$ of a locally symmetric variety
$X$ of a locally symmetric variety  ${X\unicode[STIX]{x0030A}}$ and an automorphic vector bundle
${X\unicode[STIX]{x0030A}}$ and an automorphic vector bundle 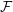 ${\mathcal{F}}$ on
${\mathcal{F}}$ on 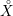 ${X\unicode[STIX]{x0030A}}$ , this refines a theorem of Goresky–Pardon. In passing we define a class of simplicial resolutions of the Baily–Borel compactification that can be used to define its mixed Hodge structure. We use this to show that the stable cohomology of the Satake (
${X\unicode[STIX]{x0030A}}$ , this refines a theorem of Goresky–Pardon. In passing we define a class of simplicial resolutions of the Baily–Borel compactification that can be used to define its mixed Hodge structure. We use this to show that the stable cohomology of the Satake (  $=$ Baily–Borel) compactification of
$=$ Baily–Borel) compactification of 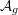 ${\mathcal{A}}_{g}$ contains nontrivial Tate extensions.
${\mathcal{A}}_{g}$ contains nontrivial Tate extensions.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2017
References
- 3
- Cited by

