Refine listing
Actions for selected content:
355 results in 14Gxx
Differential modules on p-adic polyannuli
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 19 May 2009, pp. 155-201
- Print publication:
- January 2010
-
- Article
- Export citation
Formule du conducteur pour un caractère l-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 687-717
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Independence of points on elliptic curves arising from special points on modular and Shimura curves, II: local results
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 566-602
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Local models in the ramified case. III Unitary groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 26 March 2009, pp. 507-564
- Print publication:
- July 2009
-
- Article
- Export citation
Brauer–Manin obstruction for integral points of homogeneous spaces and representation by integral quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 309-363
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Intersection theory on Shimura surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 423-475
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Desingularized fiber products of semi-stable elliptic surfaces with vanishing third Betti number
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 89-111
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
Stark–Heegner points and the Shimura correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1155-1175
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Plurigenera of general type surfaces in mixed characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 1214-1226
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Un résultat de connexité pour les variétés analytiques p-adiques: privilège et noethérianité
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 107-133
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
Counting Rational Points on Cubic Hypersurfaces
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 93-112
- Print publication:
- December 2007
-
- Article
- Export citation
Variation de la dimension relative en géométrie analytique p-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1511-1532
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
Local solutions to positive characteristic non-Archimedean differential equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1465-1477
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
On torsion of abelian varieties over large algebraic extensions of finitely generated fields: Erratum
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, p. 316
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
On torsion of abelian varieties over large algebraic extensions of finitely generated fields
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 110-116
- Print publication:
- June 1984
-
- Article
- Export citation
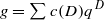 and
and 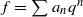 be modular forms of half-integral weight
be modular forms of half-integral weight 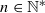 , be analytic functions over
, be analytic functions over 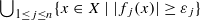 is still irreducible, provided that
is still irreducible, provided that 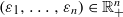 is small enough. Then, for a general
is small enough. Then, for a general 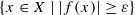 behave with regards to ε. Finally, we obtain a result concerning privileged neighbourhoods and adapt a theorem from complex analytic geometry about Noetherianity for germs of analytic functions.
behave with regards to ε. Finally, we obtain a result concerning privileged neighbourhoods and adapt a theorem from complex analytic geometry about Noetherianity for germs of analytic functions.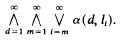
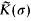 the following results hold.
the following results hold.