Refine listing
Actions for selected content:
355 results in 14Gxx
ℤ[1/p]-motivic resolution of singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 1434-1446
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Okounkov bodies of filtered linear series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 04 May 2011, pp. 1205-1229
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
A CHARACTERIZATION OF SPECIAL SUBVARIETIES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 07 March 2011, pp. 263-273
- Print publication:
- July 2011
-
- Article
- Export citation
Sur le rang des courbes elliptiques sur les corps de classes de Hilbert
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 10 February 2011, pp. 1087-1104
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
On an automorphism of Hilb[2] of certain K3 surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 1-7
-
- Article
-
- You have access
- Export citation
On the discrete logarithm problem in elliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 15 October 2010, pp. 75-104
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
The Mordell–Weil sieve: proving non-existence of rational points on curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 272-306
-
- Article
-
- You have access
- Export citation
A gap principle for dynamics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 1056-1072
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Non-archimedean canonical measures on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 21 April 2010, pp. 683-730
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
Schemes over 𝔽1 and zeta functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 21 April 2010, pp. 1383-1415
- Print publication:
- November 2010
-
- Article
-
- You have access
- Export citation
ELEMENTS OF HIGH ORDER ON FINITE FIELDS FROM ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 02 March 2010, pp. 425-429
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Analytic continuation of overconvergent Hilbert eigenforms in the totally split case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 02 February 2010, pp. 541-560
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
Conjecture de monodromie-poids pour quelques variétés de Shimura unitaires
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 367-403
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Statistics of the zeros of zeta functions in families of hyperelliptic curves over a finite field
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 81-101
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
On volumes of arithmetic line bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1447-1464
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
On the parity of ranks of Selmer groups IV. With an appendix by Jean-Pierre Wintenberger
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1351-1359
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
Chow motives without projectivity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 04 September 2009, pp. 1196-1226
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Hilbert modular forms and p-adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 21 September 2009, pp. 1081-1113
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Supersingular Kottwitz–Rapoport strata and Deligne–Lusztig varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 357-390
- Print publication:
- April 2010
-
- Article
- Export citation
The Gross–Kohnen–Zagier theorem over totally real fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 10 August 2009, pp. 1147-1162
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
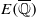 contains Heegner points of discriminant
contains Heegner points of discriminant 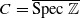 over 𝔽
over 𝔽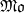 -schemes to interpret conceptually the spectral realization of zeros of
-schemes to interpret conceptually the spectral realization of zeros of 