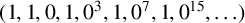 $(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
$(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
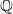 $\mathbb{Q}$
$\mathbb{Q}$
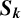 $\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
$\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
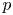 -adic $L$
-adic $L$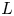 -functions
-functions