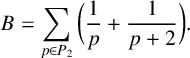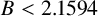1 Introduction
Brun’s constant is a fundamental constant, arising in the study of twin primes, that is, pairs of prime numbers that differ by
![]() $2$
. Set
$2$
. Set
![]() $P_2 := \{p\text { prime}:p+2 \text { is prime}\}$
. Unlike the sum of the reciprocals of all prime numbers which diverges, the sum of the reciprocals of twin primes converges to a finite value, known as Brun’s constant. This result was first established in 1919 by Brun [Reference Brun1].
$P_2 := \{p\text { prime}:p+2 \text { is prime}\}$
. Unlike the sum of the reciprocals of all prime numbers which diverges, the sum of the reciprocals of twin primes converges to a finite value, known as Brun’s constant. This result was first established in 1919 by Brun [Reference Brun1].
Brun’s proof did not yield a numerical upper bound for B. The first such bound,
![]() $B < 2.347$
, was established by Crandall and Pomerance [Reference Crandall and Pomerance3]. Since then, improvements have been made, with the current best unconditional bound
$B < 2.347$
, was established by Crandall and Pomerance [Reference Crandall and Pomerance3]. Since then, improvements have been made, with the current best unconditional bound
![]() $B < 2.288\,51$
obtained by Platt and Trudgian [Reference Platt, Trudgian, Bailey, Borwein, Brent, Burachik, Osborn, Sims and Zhu11]. Nicely [Reference Nicely9] conjectured that
$B < 2.288\,51$
obtained by Platt and Trudgian [Reference Platt, Trudgian, Bailey, Borwein, Brent, Burachik, Osborn, Sims and Zhu11]. Nicely [Reference Nicely9] conjectured that
![]() $B = 1.902\,160\,583\,209 \pm 0.000\,000\,000\,781$
, demonstrating the scope of potential improvements to be made.
$B = 1.902\,160\,583\,209 \pm 0.000\,000\,000\,781$
, demonstrating the scope of potential improvements to be made.
One approach to refining these bounds is to assume the generalised Riemann hypothesis (GRH). This method was employed by Klyve to derive the bound
![]() $B < 2.1754$
[Reference Klyve7], and it will be the approach taken here. Although our improvement is small, Klyve never published his result, and utilised numerical integration to calculate his subsequent bound on B. To our knowledge, our work represents the first mathematically rigorous upper bound on B assuming GRH.
$B < 2.1754$
[Reference Klyve7], and it will be the approach taken here. Although our improvement is small, Klyve never published his result, and utilised numerical integration to calculate his subsequent bound on B. To our knowledge, our work represents the first mathematically rigorous upper bound on B assuming GRH.
Theorem 1.1. Assume GRH. Then
![]() $B < 2.1594$
.
$B < 2.1594$
.
To achieve this, we combine previously computed values of B (up to a fixed threshold
![]() $x_0$
), along with the estimation of the tail end of the sum provided by Selberg’s sieve. This estimation proceeds by computing the intermediate sums
$x_0$
), along with the estimation of the tail end of the sum provided by Selberg’s sieve. This estimation proceeds by computing the intermediate sums
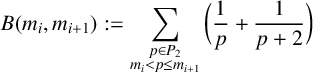 $$ \begin{align*} B(m_i,m_{i+1}):=\sum_{\substack{p \in P_2 \\ m_i<p\leq m_{i+1}}}{\bigg( \frac{1}{p} + \frac{1}{p+2}\bigg)} \end{align*} $$
$$ \begin{align*} B(m_i,m_{i+1}):=\sum_{\substack{p \in P_2 \\ m_i<p\leq m_{i+1}}}{\bigg( \frac{1}{p} + \frac{1}{p+2}\bigg)} \end{align*} $$
where
![]() $m_1 = x_0$
and
$m_1 = x_0$
and
![]() $i=1,\ldots , k$
. These sums are then combined to evaluate
$i=1,\ldots , k$
. These sums are then combined to evaluate
![]() $B(m_1,\infty )$
.
$B(m_1,\infty )$
.
This intermediate sum approach is advantageous due to its flexibility, as different methods of estimating B may yield tighter bounds over different regions. By combining these results, a sharper overall bound can be obtained. To facilitate further improvements, we provide explicit bounds for each
![]() $B(m_i,m_{i+1})$
.
$B(m_i,m_{i+1})$
.
The structure of this paper is as follows. Section 2 introduces the sieve framework, defines key notation, and derives a bound for the twin prime counting function. Section 3 extends this bound to Brun’s constant using partial summation. Section 4 focuses on parameter optimisation and presents the numerical computations. Finally, Section 5 discusses potential refinements and further improvements to this method.
2 Upper bound on
 $\pi _2(x)$
$\pi _2(x)$
To calculate B, we require an upper bound on the twin prime counting function
![]() $\pi _2(x) := \#\{p \text { prime}: p+2 \text { also prime}\}$
. We derive this bound using Selberg’s sieve by sieving on the set of odd numbers n such that
$\pi _2(x) := \#\{p \text { prime}: p+2 \text { also prime}\}$
. We derive this bound using Selberg’s sieve by sieving on the set of odd numbers n such that
![]() $n-2$
is prime. If n is removed by the sieve (that is, n is not prime), then
$n-2$
is prime. If n is removed by the sieve (that is, n is not prime), then
![]() $(n-2,n)$
cannot form a twin prime pair.
$(n-2,n)$
cannot form a twin prime pair.
2.1 Preliminaries
For an introduction to Selberg’s sieve, see [Reference Halberstam and Richert5]. We begin by defining some preliminary notation. Our set of twin prime candidates is given by
and our set of sieving primes by
We will be sieving using odd primes less than or equal to z, and so we set
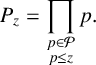 $$ \begin{align*} P_z= \prod_{\substack{p \in\mathcal{P}\\ p\leq z}}{p}. \end{align*} $$
$$ \begin{align*} P_z= \prod_{\substack{p \in\mathcal{P}\\ p\leq z}}{p}. \end{align*} $$
Next,
![]() $\mathcal {A}_d$
is the set of twin prime candidates that are divisible by a specific prime d, and
$\mathcal {A}_d$
is the set of twin prime candidates that are divisible by a specific prime d, and
By the prime number theorem in arithmetic progressions, we can estimate
![]() $\pi (x;d,-2)$
by
$\pi (x;d,-2)$
by
![]() ${\text {li}(x)}/{\varphi (d)}$
, and so we define the error in our estimation to be
${\text {li}(x)}/{\varphi (d)}$
, and so we define the error in our estimation to be
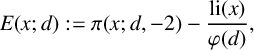 $$ \begin{align*} E(x;d):= \pi(x;d,-2) - \frac{\text{li}(x)}{\varphi(d)}, \end{align*} $$
$$ \begin{align*} E(x;d):= \pi(x;d,-2) - \frac{\text{li}(x)}{\varphi(d)}, \end{align*} $$
where
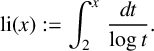 $$ \begin{align*} \text{li}(x) := \int_2^x\,\frac{dt}{\log{t}}. \end{align*} $$
$$ \begin{align*} \text{li}(x) := \int_2^x\,\frac{dt}{\log{t}}. \end{align*} $$
As we take li to be truncated at 2, it will be useful to define the offset as
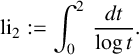 $$ \begin{align*} \text{li}_2:=\int_0^2\,\frac{dt}{\log{t}}. \end{align*} $$
$$ \begin{align*} \text{li}_2:=\int_0^2\,\frac{dt}{\log{t}}. \end{align*} $$
The twin prime constant is
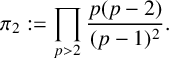 $$ \begin{align*} \pi_2 := \prod_{p>2}\frac{p(p-2)}{(p-1)^2}. \end{align*} $$
$$ \begin{align*} \pi_2 := \prod_{p>2}\frac{p(p-2)}{(p-1)^2}. \end{align*} $$
Following Klyve [Reference Klyve7, page 128], we take
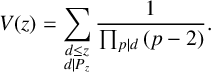 $$ \begin{align*} V(z) = \sum_{\substack{d \leq z \\ d|P_z}}{\frac{1}{\prod_{p|d}{(p-2)}}}. \end{align*} $$
$$ \begin{align*} V(z) = \sum_{\substack{d \leq z \\ d|P_z}}{\frac{1}{\prod_{p|d}{(p-2)}}}. \end{align*} $$
And finally, we set
Theorem 2.1 [Reference Klyve7, Theorem 5.7].
For
![]() $0<z<x$
,
$0<z<x$
,
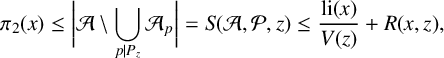 $$ \begin{align*} \pi_2(x) \leq \bigg|\mathcal{A} \setminus \bigcup_{p|P_z} \mathcal{A}_p\bigg| = S(\mathcal{A},\mathcal{P}, z) \leq \frac{\mathrm{li}(x)}{V(z)}+ R(x,z), \end{align*} $$
$$ \begin{align*} \pi_2(x) \leq \bigg|\mathcal{A} \setminus \bigcup_{p|P_z} \mathcal{A}_p\bigg| = S(\mathcal{A},\mathcal{P}, z) \leq \frac{\mathrm{li}(x)}{V(z)}+ R(x,z), \end{align*} $$
where we have defined
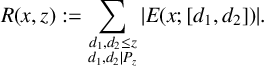 $$ \begin{align*} R(x,z):= \sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{|E(x;[d_1,d_2])|}. \end{align*} $$
$$ \begin{align*} R(x,z):= \sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{|E(x;[d_1,d_2])|}. \end{align*} $$
2.2 Bounding
 $V^{-1}(z)$
$V^{-1}(z)$
We need to provide an upper bound on
![]() $V^{-1}(z)$
for all z. As z increases, computing
$V^{-1}(z)$
for all z. As z increases, computing
![]() $V(z)$
directly becomes infeasible, requiring a trade-off between accuracy and efficiency. To address this, we will consider three separate intervals (separated by values
$V(z)$
directly becomes infeasible, requiring a trade-off between accuracy and efficiency. To address this, we will consider three separate intervals (separated by values
![]() $L_1$
and
$L_1$
and
![]() $L_2$
), with different bounds on
$L_2$
), with different bounds on
![]() $V(z)$
for each interval. For our calculations, we set
$V(z)$
for each interval. For our calculations, we set
![]() $L_1 = 10^8$
and
$L_1 = 10^8$
and
![]() $L_2 = 10^{10}$
.
$L_2 = 10^{10}$
.
For the first interval (
![]() $z < L_1$
), we compute
$z < L_1$
), we compute
![]() $V(z)$
exactly. For the second interval (
$V(z)$
exactly. For the second interval (
![]() $L_1 < z \leq L_2$
), we compute
$L_1 < z \leq L_2$
), we compute
![]() $V(z')$
exactly, where
$V(z')$
exactly, where
![]() $z' \in \{L_1<z\leq L_2: z=k\cdot 10^4, k \in \mathbb {N}\}$
(that is, every
$z' \in \{L_1<z\leq L_2: z=k\cdot 10^4, k \in \mathbb {N}\}$
(that is, every
![]() $10^4$
th number). For the values of z such that
$10^4$
th number). For the values of z such that
![]() $10^4 \nmid z$
, we can round z down to the nearest
$10^4 \nmid z$
, we can round z down to the nearest
![]() $z'$
to give an upper bound on
$z'$
to give an upper bound on
![]() $V^{-1}(z)$
. For the third interval, we will use the approximation of
$V^{-1}(z)$
. For the third interval, we will use the approximation of
![]() $V(z)$
derived in [Reference Klyve7, Section 5.5.2], namely
$V(z)$
derived in [Reference Klyve7, Section 5.5.2], namely
where
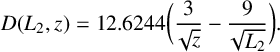 $$ \begin{align*} D(L_2,z) = 12.6244\bigg(\frac{3}{\sqrt{z}} - \frac{9}{\sqrt{L_2}}\bigg). \end{align*} $$
$$ \begin{align*} D(L_2,z) = 12.6244\bigg(\frac{3}{\sqrt{z}} - \frac{9}{\sqrt{L_2}}\bigg). \end{align*} $$
The following lemma summarises these arrangements.
Lemma 2.2. For any z, we have
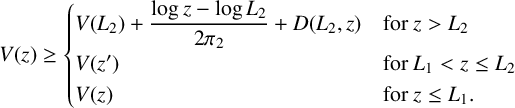 $$ \begin{align*}V(z) \geq \begin{cases} V(L_2) + \dfrac{\log{z}-\log{L_2}}{2\pi_2} + D(L_2,z) & \mbox{for }z> L_2\\ V(z') & \mbox{for }L_1 <z \leq L_2 \\ V(z) & \mbox{for } z\leq L_1. \end{cases}\end{align*} $$
$$ \begin{align*}V(z) \geq \begin{cases} V(L_2) + \dfrac{\log{z}-\log{L_2}}{2\pi_2} + D(L_2,z) & \mbox{for }z> L_2\\ V(z') & \mbox{for }L_1 <z \leq L_2 \\ V(z) & \mbox{for } z\leq L_1. \end{cases}\end{align*} $$
2.3 Bounding
 $R(x,z)$
$R(x,z)$
Next, we need an upper bound on
![]() $R(x,z)$
for all x and z. We will start by proving an inequality that will allow us to bound one of the terms of
$R(x,z)$
for all x and z. We will start by proving an inequality that will allow us to bound one of the terms of
![]() $R(x,z)$
. This inequality holds for any fixed prime p, but becomes less useful as the size of p increases relative to the size of z. We have excluded some slight optimisations on the order of
$R(x,z)$
. This inequality holds for any fixed prime p, but becomes less useful as the size of p increases relative to the size of z. We have excluded some slight optimisations on the order of
![]() $z^{1/2}$
for the sake of readability, and the range of permissible values of z can be lowered at a similar cost. For our case, we will be setting
$z^{1/2}$
for the sake of readability, and the range of permissible values of z can be lowered at a similar cost. For our case, we will be setting
![]() $p=2$
.
$p=2$
.
Proposition 2.3. Let p be a prime and
![]() $z \geq 2\,768\,896$
. Then
$z \geq 2\,768\,896$
. Then
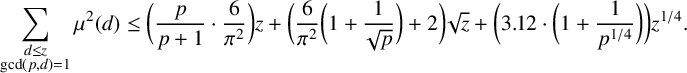 $$ \begin{align*} \sum_{\substack{d \leq z \\ \mathrm{gcd}(p,d)=1}}{\mu^2(d)} \leq \bigg(\frac{p}{p+1}\cdot \frac{6}{\pi^2}\bigg)z + \bigg( \frac{6}{\pi^2}\bigg(1+\frac{1}{\sqrt{p}}\bigg)+2\bigg)\sqrt{z} + \bigg(3.12 \cdot\bigg(1+\frac{1}{p^{1/4}}\bigg)\bigg)z^{1/4}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{d \leq z \\ \mathrm{gcd}(p,d)=1}}{\mu^2(d)} \leq \bigg(\frac{p}{p+1}\cdot \frac{6}{\pi^2}\bigg)z + \bigg( \frac{6}{\pi^2}\bigg(1+\frac{1}{\sqrt{p}}\bigg)+2\bigg)\sqrt{z} + \bigg(3.12 \cdot\bigg(1+\frac{1}{p^{1/4}}\bigg)\bigg)z^{1/4}. \end{align*} $$
Proof. To start, note that we can write
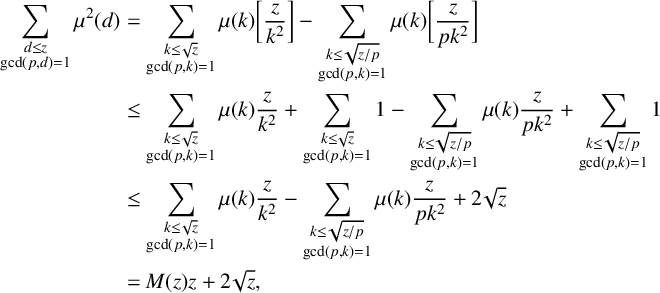 $$ \begin{align*} \sum_{\substack{d \leq z \\ \mathrm{gcd}(p,d)=1}}{\mu^2(d)} &= \sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\bigg[\frac{z}{k^2}\bigg] - \sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\bigg[\frac{z}{pk^2}\bigg] \\ &\leq \sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\frac{z}{k^2} + \sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}1 - \sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\frac{z}{pk^2} +\sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}1\\ &\leq \sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\frac{z}{k^2} - \sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\frac{z}{pk^2} + 2 \sqrt{z}\\ &= M(z)z + 2 \sqrt{z}, \end{align*} $$
$$ \begin{align*} \sum_{\substack{d \leq z \\ \mathrm{gcd}(p,d)=1}}{\mu^2(d)} &= \sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\bigg[\frac{z}{k^2}\bigg] - \sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\bigg[\frac{z}{pk^2}\bigg] \\ &\leq \sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\frac{z}{k^2} + \sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}1 - \sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\frac{z}{pk^2} +\sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}1\\ &\leq \sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\frac{z}{k^2} - \sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\mu(k)\frac{z}{pk^2} + 2 \sqrt{z}\\ &= M(z)z + 2 \sqrt{z}, \end{align*} $$
where we have taken
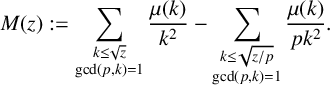 $$ \begin{align*} M(z) :=\sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{k^2} - \sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{pk^2}. \end{align*} $$
$$ \begin{align*} M(z) :=\sum_{\substack{k \leq \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{k^2} - \sum_{\substack{k \leq \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{pk^2}. \end{align*} $$
Also, for
![]() $p'$
any prime number,
$p'$
any prime number,
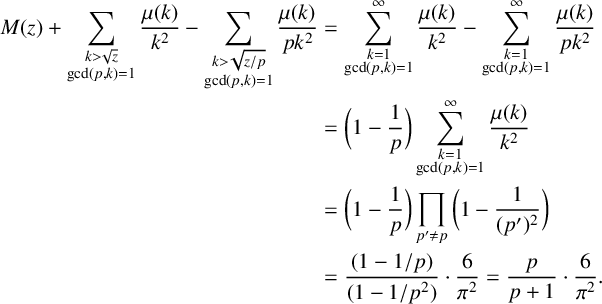 $$ \begin{align*} M(z) + \sum_{\substack{k> \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{k^2} - \sum_{\substack{k > \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{pk^2} &= \sum_{\substack{k=1 \\ \mathrm{gcd}(p,k)=1}}^{\infty}\frac{\mu(k)}{k^2} - \sum_{\substack{k =1 \\ \mathrm{gcd}(p,k)=1}}^{\infty}\frac{\mu(k)}{pk^2} \\ &=\bigg(1-\frac{1}{p}\bigg)\sum_{\substack{k=1 \\ \mathrm{gcd}(p,k)=1}}^{\infty}\frac{\mu(k)}{k^2} \\ &=\bigg(1-\frac{1}{p}\bigg)\prod_{p' \neq p}\bigg(1-\frac{1}{(p')^2}\bigg)\\ &=\frac{(1-{1}/{p})}{(1-{1}/{p^2})} \cdot \frac{6}{\pi^2} =\frac{p}{p+1} \cdot \frac{6}{\pi^2}. \end{align*} $$
$$ \begin{align*} M(z) + \sum_{\substack{k> \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{k^2} - \sum_{\substack{k > \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{pk^2} &= \sum_{\substack{k=1 \\ \mathrm{gcd}(p,k)=1}}^{\infty}\frac{\mu(k)}{k^2} - \sum_{\substack{k =1 \\ \mathrm{gcd}(p,k)=1}}^{\infty}\frac{\mu(k)}{pk^2} \\ &=\bigg(1-\frac{1}{p}\bigg)\sum_{\substack{k=1 \\ \mathrm{gcd}(p,k)=1}}^{\infty}\frac{\mu(k)}{k^2} \\ &=\bigg(1-\frac{1}{p}\bigg)\prod_{p' \neq p}\bigg(1-\frac{1}{(p')^2}\bigg)\\ &=\frac{(1-{1}/{p})}{(1-{1}/{p^2})} \cdot \frac{6}{\pi^2} =\frac{p}{p+1} \cdot \frac{6}{\pi^2}. \end{align*} $$
Now we can bound the difference
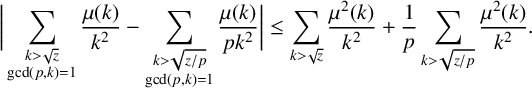 $$ \begin{align*} \bigg|\sum_{\substack{k> \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{k^2} - \sum_{\substack{k > \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{pk^2} \bigg| \leq \sum_{k > \sqrt{z}}\frac{\mu^2(k)}{k^2} + \frac{1}{p}\sum_{k > \sqrt{{z}/{p}} }\frac{\mu^2(k)}{k^2}. \end{align*} $$
$$ \begin{align*} \bigg|\sum_{\substack{k> \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{k^2} - \sum_{\substack{k > \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{pk^2} \bigg| \leq \sum_{k > \sqrt{z}}\frac{\mu^2(k)}{k^2} + \frac{1}{p}\sum_{k > \sqrt{{z}/{p}} }\frac{\mu^2(k)}{k^2}. \end{align*} $$
We now apply explicit bounds on the square-free summation function provided in [Reference Cohen, Dress, Daboussi, Deshouillers and Liardet2], in conjunction with partial summation, to note that
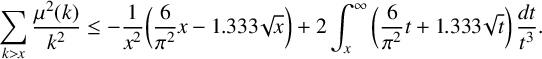 $$ \begin{align*} \sum_{k> x}\frac{\mu^2(k)}{k^2} \leq -\frac{1}{x^2}\bigg(\frac{6}{\pi^2}x - 1.333\sqrt{x}\bigg) + 2\int_{x}^{\infty} \bigg(\frac{6}{\pi^2}t + 1.333\sqrt{t}\bigg) \,\frac{dt}{t^3}. \end{align*} $$
$$ \begin{align*} \sum_{k> x}\frac{\mu^2(k)}{k^2} \leq -\frac{1}{x^2}\bigg(\frac{6}{\pi^2}x - 1.333\sqrt{x}\bigg) + 2\int_{x}^{\infty} \bigg(\frac{6}{\pi^2}t + 1.333\sqrt{t}\bigg) \,\frac{dt}{t^3}. \end{align*} $$
Applying this substitution, and simplifying terms, we conclude that
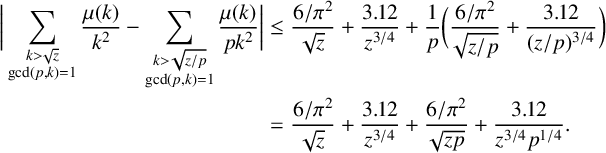 $$ \begin{align*} \bigg|\sum_{\substack{k> \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{k^2}- \sum_{\substack{k > \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{pk^2} \bigg| &\leq \frac{{6}/{\pi^2}}{\sqrt{z}} + \frac{3.12}{z^{3/4}} + \frac{1}{p}\bigg(\frac{{6}/{\pi^2}}{\sqrt{{z}/{p}}} + \frac{3.12}{({z}/{p})^{3/4}} \bigg)\\ &= \frac{{6}/{\pi^2}}{\sqrt{z}} + \frac{3.12}{z^{3/4}} + \frac{{6}/{\pi^2}}{\sqrt{zp}} + \frac{3.12}{z^{3/4}p^{1/4}}. \end{align*} $$
$$ \begin{align*} \bigg|\sum_{\substack{k> \sqrt{z} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{k^2}- \sum_{\substack{k > \sqrt{{z}/{p}} \\ \mathrm{gcd}(p,k)=1}}\frac{\mu(k)}{pk^2} \bigg| &\leq \frac{{6}/{\pi^2}}{\sqrt{z}} + \frac{3.12}{z^{3/4}} + \frac{1}{p}\bigg(\frac{{6}/{\pi^2}}{\sqrt{{z}/{p}}} + \frac{3.12}{({z}/{p})^{3/4}} \bigg)\\ &= \frac{{6}/{\pi^2}}{\sqrt{z}} + \frac{3.12}{z^{3/4}} + \frac{{6}/{\pi^2}}{\sqrt{zp}} + \frac{3.12}{z^{3/4}p^{1/4}}. \end{align*} $$
Combining this result with the first inequality proves the lemma.
In a similar manner to
![]() $V(z)$
, the sum
$V(z)$
, the sum
![]() $\sum _{ {d \leq z,\, \mathrm {gcd}(2,d)=1}}{\mu ^2(d)}$
becomes infeasible to compute for large values of z. We employ a similar technique of approximating
$\sum _{ {d \leq z,\, \mathrm {gcd}(2,d)=1}}{\mu ^2(d)}$
becomes infeasible to compute for large values of z. We employ a similar technique of approximating
![]() $\sum _{{d \leq z, \,\mathrm {gcd}(2,d)=1}}{\mu ^2(d)}$
for z larger than a specific cut-off value
$\sum _{{d \leq z, \,\mathrm {gcd}(2,d)=1}}{\mu ^2(d)}$
for z larger than a specific cut-off value
![]() $L_3$
(using Proposition 2.3), and calculating it exactly for the remaining values. We take
$L_3$
(using Proposition 2.3), and calculating it exactly for the remaining values. We take
![]() $L_3=10^7$
for our calculations.
$L_3=10^7$
for our calculations.
Lemma 2.4. For any z,
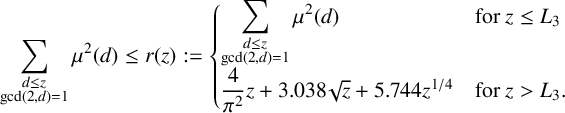 $$ \begin{align*} &\sum_{\substack{d \leq z \\ \mathrm{gcd}(2,d)=1}}{\mu^2(d)} \leq r(z):= \begin{cases} \displaystyle\sum_{\substack{d \leq z \\ \mathrm{gcd}(2,d)=1}}{\mu^2(d)} & \mbox{for } z \leq L_3 \\ \dfrac{4}{\pi^2}z + 3.038\sqrt{z} + 5.744z^{1/4} & \mbox{for } z>L_3. \end{cases} \end{align*} $$
$$ \begin{align*} &\sum_{\substack{d \leq z \\ \mathrm{gcd}(2,d)=1}}{\mu^2(d)} \leq r(z):= \begin{cases} \displaystyle\sum_{\substack{d \leq z \\ \mathrm{gcd}(2,d)=1}}{\mu^2(d)} & \mbox{for } z \leq L_3 \\ \dfrac{4}{\pi^2}z + 3.038\sqrt{z} + 5.744z^{1/4} & \mbox{for } z>L_3. \end{cases} \end{align*} $$
Theorem 2.5. Assuming GRH, for
![]() $x \geq 4\cdot 10^{18}$
and
$x \geq 4\cdot 10^{18}$
and
![]() $z<x^{{1}/{4}}$
,
$z<x^{{1}/{4}}$
,
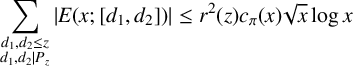 $$ \begin{align*} \sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{|E(x;[d_1,d_2])|} \leq r^2(z)c_\pi(x)\sqrt{x}\log{x} \end{align*} $$
$$ \begin{align*} \sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{|E(x;[d_1,d_2])|} \leq r^2(z)c_\pi(x)\sqrt{x}\log{x} \end{align*} $$
where
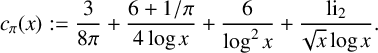 $$ \begin{align*} &c_\pi(x) := \frac{3}{8\pi} + \frac{6+1/\pi}{4\log{x}} + \frac{6}{\log^2{x}} + \frac{\mathrm{li}_2}{\sqrt{x}\log{x}}. \end{align*} $$
$$ \begin{align*} &c_\pi(x) := \frac{3}{8\pi} + \frac{6+1/\pi}{4\log{x}} + \frac{6}{\log^2{x}} + \frac{\mathrm{li}_2}{\sqrt{x}\log{x}}. \end{align*} $$
Proof. We will use [Reference Johnston and Starichkova6, Lemma 5.1] to bound under GRH, noting that for
![]() $z<x^{{1}/{4}}$
,
$z<x^{{1}/{4}}$
,
![]() $[d_1,d_2]<d_1d_2 < z^2 < \sqrt {x}$
. Thus, for
$[d_1,d_2]<d_1d_2 < z^2 < \sqrt {x}$
. Thus, for
![]() $x \geq 4\cdot 10^{18}$
and
$x \geq 4\cdot 10^{18}$
and
![]() $z<x^{{1}/{4}}$
,
$z<x^{{1}/{4}}$
,
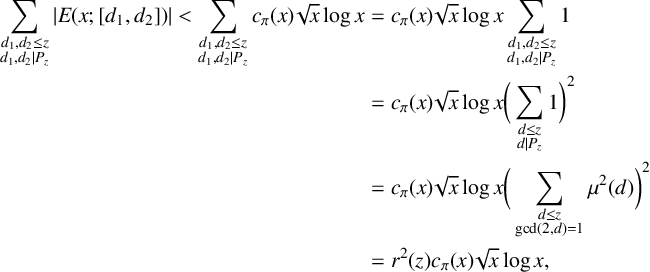 $$ \begin{align*} \sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{|E(x;[d_1,d_2])|} < \sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{c_\pi(x)\sqrt{x}\log{x}}&= c_\pi(x)\sqrt{x}\log{x}\sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{1} \\ &=c_\pi(x)\sqrt{x}\log{x}\bigg(\sum_{\substack{d \leq z \\ d| P_z}}{1}\bigg)^2 \\ &=c_\pi(x)\sqrt{x}\log{x}\bigg(\sum_{\substack{d \leq z \\ \gcd(2,d)=1}}{\mu^2(d)}\bigg)^2 \\ &=r^2(z)c_\pi(x)\sqrt{x}\log{x}, \end{align*} $$
$$ \begin{align*} \sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{|E(x;[d_1,d_2])|} < \sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{c_\pi(x)\sqrt{x}\log{x}}&= c_\pi(x)\sqrt{x}\log{x}\sum_{\substack{d_1, d_2 \leq z \\ d_1,d_2 | P_z}}{1} \\ &=c_\pi(x)\sqrt{x}\log{x}\bigg(\sum_{\substack{d \leq z \\ d| P_z}}{1}\bigg)^2 \\ &=c_\pi(x)\sqrt{x}\log{x}\bigg(\sum_{\substack{d \leq z \\ \gcd(2,d)=1}}{\mu^2(d)}\bigg)^2 \\ &=r^2(z)c_\pi(x)\sqrt{x}\log{x}, \end{align*} $$
by applying Lemma 2.4 on the second last line.
3 Upper bound on B
From [Reference Platt, Trudgian, Bailey, Borwein, Brent, Burachik, Osborn, Sims and Zhu11, Lemma 6],
Now, using our bound on
![]() $\pi _2(x)$
, we can apply partial summation to calculate
$\pi _2(x)$
, we can apply partial summation to calculate
![]() $B(m_1,\infty )$
. Let
$B(m_1,\infty )$
. Let
![]() $z_i$
be fixed for each interval
$z_i$
be fixed for each interval
![]() $[m_i,m_{i+1}]$
(the values of each
$[m_i,m_{i+1}]$
(the values of each
![]() $z_i$
and the intervals
$z_i$
and the intervals
![]() $[m_i,m_{i+1}]$
will be determined later).
$[m_i,m_{i+1}]$
will be determined later).
Lemma 3.1. Assuming GRH, for
![]() $m_1 \geq 4\cdot 10^{18}$
and
$m_1 \geq 4\cdot 10^{18}$
and
![]() $z_i<m_i^{{1}/{4}}$
,
$z_i<m_i^{{1}/{4}}$
,
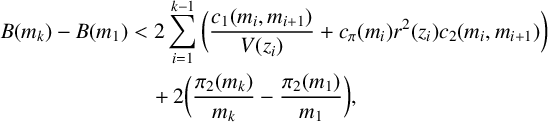 $$ \begin{align*} B(m_k)-B(m_1) &< 2 \sum_{i=1}^{k-1}\bigg(\frac{c_1(m_i,m_{i+1})}{V(z_i)} + c_\pi(m_i)r^2(z_i)c_2(m_i,m_{i+1}) \bigg) \\ &\quad +2\bigg(\frac{\pi_2(m_k)}{m_k} -\frac{\pi_2(m_1)}{m_1} \bigg), \end{align*} $$
$$ \begin{align*} B(m_k)-B(m_1) &< 2 \sum_{i=1}^{k-1}\bigg(\frac{c_1(m_i,m_{i+1})}{V(z_i)} + c_\pi(m_i)r^2(z_i)c_2(m_i,m_{i+1}) \bigg) \\ &\quad +2\bigg(\frac{\pi_2(m_k)}{m_k} -\frac{\pi_2(m_1)}{m_1} \bigg), \end{align*} $$
where
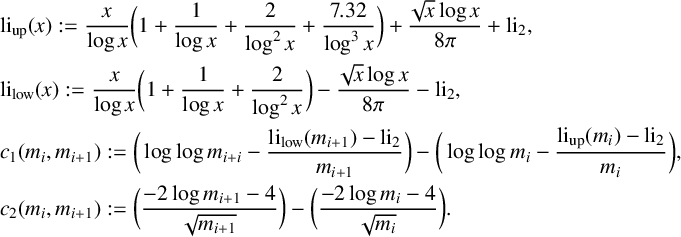 $$ \begin{align*} &\mathrm{li}_{\mathrm{up}}(x) := \frac{x}{\log{x}}\bigg(1 + \frac{1}{\log{x}} + \frac{2}{\log^2{x}} + \frac{7.32}{\log^3{x}} \bigg) + \frac{\sqrt{x}\log{x}}{8\pi} + \mathrm{li}_2, \\ &\mathrm{li}_{\mathrm{low}}(x) := \frac{x}{\log{x}}\bigg(1 + \frac{1}{\log{x}} + \frac{2}{\log^2{x}} \bigg) - \frac{\sqrt{x}\log{x}}{8\pi} - \mathrm{li}_2, \\ & c_1(m_i,m_{i+1}) := \bigg(\log{\log{m_{i+i}}}- \frac{\mathrm{li}_{\mathrm{low}}(m_{i+1}) - \mathrm{li}_2}{m_{i+1}}\bigg) -\bigg(\log{\log{m_{i}}}- \frac{\mathrm{li}_{\mathrm{up}}(m_{i}) - \mathrm{li}_2}{m_{i}}\bigg),\\ & c_2(m_i,m_{i+1}) := \bigg( \frac{-2\log{m_{i+1}}-4}{\sqrt{m_{i+1}}} \bigg) - \bigg( \frac{-2\log{m_i}-4}{\sqrt{m_i}} \bigg). \end{align*} $$
$$ \begin{align*} &\mathrm{li}_{\mathrm{up}}(x) := \frac{x}{\log{x}}\bigg(1 + \frac{1}{\log{x}} + \frac{2}{\log^2{x}} + \frac{7.32}{\log^3{x}} \bigg) + \frac{\sqrt{x}\log{x}}{8\pi} + \mathrm{li}_2, \\ &\mathrm{li}_{\mathrm{low}}(x) := \frac{x}{\log{x}}\bigg(1 + \frac{1}{\log{x}} + \frac{2}{\log^2{x}} \bigg) - \frac{\sqrt{x}\log{x}}{8\pi} - \mathrm{li}_2, \\ & c_1(m_i,m_{i+1}) := \bigg(\log{\log{m_{i+i}}}- \frac{\mathrm{li}_{\mathrm{low}}(m_{i+1}) - \mathrm{li}_2}{m_{i+1}}\bigg) -\bigg(\log{\log{m_{i}}}- \frac{\mathrm{li}_{\mathrm{up}}(m_{i}) - \mathrm{li}_2}{m_{i}}\bigg),\\ & c_2(m_i,m_{i+1}) := \bigg( \frac{-2\log{m_{i+1}}-4}{\sqrt{m_{i+1}}} \bigg) - \bigg( \frac{-2\log{m_i}-4}{\sqrt{m_i}} \bigg). \end{align*} $$
Proof. We have
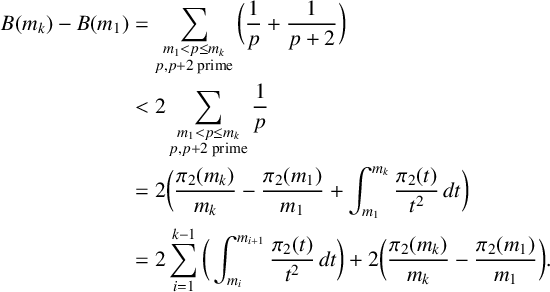 $$ \begin{align*} B(m_k)-B(m_1) &= \sum_{\substack{m_1<p\leq m_k \\ p,p+2 \text{ prime}}}{\bigg(\frac{1}{p} + \frac{1}{p+2}\bigg)}\\ &< 2\sum_{\substack{m_1<p\leq m_k \\ p,p+2 \text{ prime}}}{\frac{1}{p}} \\ &=2\bigg(\frac{\pi_2(m_k)}{m_k} -\frac{\pi_2(m_1)}{m_1} + \int_{m_1}^{m_k}{\frac{\pi_2(t)}{t^2}}\,dt\bigg) \\ &=2\sum_{i=1}^{k-1}\bigg( \int_{m_i}^{m_{i+1}}{\frac{\pi_2(t)}{t^2}}\,dt \bigg) + 2\bigg(\frac{\pi_2(m_k)}{m_k} -\frac{\pi_2(m_1)}{m_1} \bigg). \end{align*} $$
$$ \begin{align*} B(m_k)-B(m_1) &= \sum_{\substack{m_1<p\leq m_k \\ p,p+2 \text{ prime}}}{\bigg(\frac{1}{p} + \frac{1}{p+2}\bigg)}\\ &< 2\sum_{\substack{m_1<p\leq m_k \\ p,p+2 \text{ prime}}}{\frac{1}{p}} \\ &=2\bigg(\frac{\pi_2(m_k)}{m_k} -\frac{\pi_2(m_1)}{m_1} + \int_{m_1}^{m_k}{\frac{\pi_2(t)}{t^2}}\,dt\bigg) \\ &=2\sum_{i=1}^{k-1}\bigg( \int_{m_i}^{m_{i+1}}{\frac{\pi_2(t)}{t^2}}\,dt \bigg) + 2\bigg(\frac{\pi_2(m_k)}{m_k} -\frac{\pi_2(m_1)}{m_1} \bigg). \end{align*} $$
The value of
![]() ${\pi _2(m_k)}/{m_k}$
will cancel in a further calculation, and the value of
${\pi _2(m_k)}/{m_k}$
will cancel in a further calculation, and the value of
![]() ${\pi _2(m_1)}/{m_1}$
can be calculated exactly using the computations performed by Oliveira e Silva [Reference Oliveira e Silva10]. For the remaining term, we proceed by
${\pi _2(m_1)}/{m_1}$
can be calculated exactly using the computations performed by Oliveira e Silva [Reference Oliveira e Silva10]. For the remaining term, we proceed by
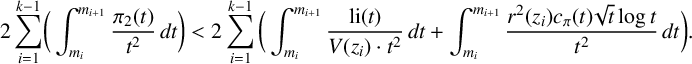 $$ \begin{align*} 2 \sum_{i=1}^{k-1}&\bigg( \int_{m_i}^{m_{i+1}}{\frac{\pi_2(t)}{t^2}} \,dt\bigg) < 2 \sum_{i=1}^{k-1}\bigg( \int_{m_i}^{m_{i+1}}{\frac{\mathrm{li}(t)}{V(z_i)\cdot t^2}}\,dt + \int_{m_i}^{m_{i+1}}{\frac{ r^2(z_i)c_\pi(t)\sqrt{t}\log{t}}{t^2}}\,dt \bigg). \end{align*} $$
$$ \begin{align*} 2 \sum_{i=1}^{k-1}&\bigg( \int_{m_i}^{m_{i+1}}{\frac{\pi_2(t)}{t^2}} \,dt\bigg) < 2 \sum_{i=1}^{k-1}\bigg( \int_{m_i}^{m_{i+1}}{\frac{\mathrm{li}(t)}{V(z_i)\cdot t^2}}\,dt + \int_{m_i}^{m_{i+1}}{\frac{ r^2(z_i)c_\pi(t)\sqrt{t}\log{t}}{t^2}}\,dt \bigg). \end{align*} $$
We now apply some simplifications to these integrals to allow us to compute them analytically. Firstly, note that
![]() $V(z_i)$
and
$V(z_i)$
and
![]() $r(z_i)$
are fixed for each interval
$r(z_i)$
are fixed for each interval
![]() $[m_i,m_{i+1}]$
. Also, note that
$[m_i,m_{i+1}]$
. Also, note that
![]() $c_{\pi }(t)$
is monotonically decreasing and so
$c_{\pi }(t)$
is monotonically decreasing and so
![]() $c_{\pi }(t) \leq c_{\pi }(m_i)$
for
$c_{\pi }(t) \leq c_{\pi }(m_i)$
for
![]() $x \in [m_i,m_{i+1}]$
. Consequently,
$x \in [m_i,m_{i+1}]$
. Consequently,
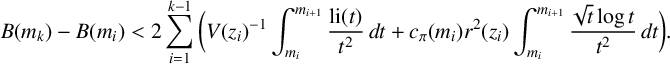 $$ \begin{align*} B(m_k)-B(m_i)<2 \sum_{i=1}^{k-1}\bigg( V(z_i)^{-1}\int_{m_i}^{m_{i+1}}{\frac{\mathrm{li}(t)}{t^2}}\,dt+ c_\pi(m_i)r^2(z_i)\int_{m_i}^{m_{i+1}}{\frac{ \sqrt{t}\log{t}}{t^2}}\,dt \bigg). \end{align*} $$
$$ \begin{align*} B(m_k)-B(m_i)<2 \sum_{i=1}^{k-1}\bigg( V(z_i)^{-1}\int_{m_i}^{m_{i+1}}{\frac{\mathrm{li}(t)}{t^2}}\,dt+ c_\pi(m_i)r^2(z_i)\int_{m_i}^{m_{i+1}}{\frac{ \sqrt{t}\log{t}}{t^2}}\,dt \bigg). \end{align*} $$
In computing the integral we note that
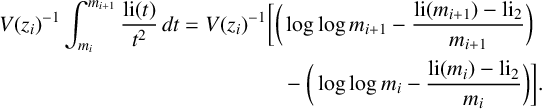 $$ \begin{align*} V(z_i)^{-1}\int_{m_i}^{m_{i+1}}{\frac{\text{li}(t)}{t^2}}\,dt = V(z_i)^{-1}\bigg[\bigg(&\log{\log{m_{i+1}}}- \frac{\text{li}(m_{i+1}) - \text{li}_2}{m_{i+1}}\bigg)\\ & - \bigg(\log{\log{m_{i}}}- \frac{\text{li}(m_{i}) - \text{li}_2}{m_{i}}\bigg)\bigg]. \end{align*} $$
$$ \begin{align*} V(z_i)^{-1}\int_{m_i}^{m_{i+1}}{\frac{\text{li}(t)}{t^2}}\,dt = V(z_i)^{-1}\bigg[\bigg(&\log{\log{m_{i+1}}}- \frac{\text{li}(m_{i+1}) - \text{li}_2}{m_{i+1}}\bigg)\\ & - \bigg(\log{\log{m_{i}}}- \frac{\text{li}(m_{i}) - \text{li}_2}{m_{i}}\bigg)\bigg]. \end{align*} $$
To avoid computing li
![]() $(x)$
directly, we use Schoenfeld’s bound on
$(x)$
directly, we use Schoenfeld’s bound on
![]() $|\pi (x)-\text {li}(x)|$
assuming the Riemann hypothesis [Reference Schoenfeld13, (6.18)], and Dusart’s bounds on
$|\pi (x)-\text {li}(x)|$
assuming the Riemann hypothesis [Reference Schoenfeld13, (6.18)], and Dusart’s bounds on
![]() $\pi (x)$
[Reference Dusart4, Theorem 5.1 and Corollary 5.2], to find (for
$\pi (x)$
[Reference Dusart4, Theorem 5.1 and Corollary 5.2], to find (for
![]() $x \geq 4 \cdot 10^9$
) that
$x \geq 4 \cdot 10^9$
) that
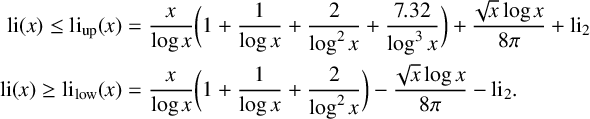 $$ \begin{align*} \text{li}(x) \leq \text{li}_{\text{up}}(x) & = \frac{x}{\log{x}}\bigg(1 + \frac{1}{\log{x}} + \frac{2}{\log^2{x}} + \frac{7.32}{\log^3{x}} \bigg) + \frac{\sqrt{x}\log{x}}{8\pi} + \text{li}_2 \\ \text{li}(x) \geq \text{li}_{\text{low}}(x) & = \frac{x}{\log{x}}\bigg(1 + \frac{1}{\log{x}} + \frac{2}{\log^2{x}} \bigg) - \frac{\sqrt{x}\log{x}}{8\pi} - \text{li}_2. \end{align*} $$
$$ \begin{align*} \text{li}(x) \leq \text{li}_{\text{up}}(x) & = \frac{x}{\log{x}}\bigg(1 + \frac{1}{\log{x}} + \frac{2}{\log^2{x}} + \frac{7.32}{\log^3{x}} \bigg) + \frac{\sqrt{x}\log{x}}{8\pi} + \text{li}_2 \\ \text{li}(x) \geq \text{li}_{\text{low}}(x) & = \frac{x}{\log{x}}\bigg(1 + \frac{1}{\log{x}} + \frac{2}{\log^2{x}} \bigg) - \frac{\sqrt{x}\log{x}}{8\pi} - \text{li}_2. \end{align*} $$
And so
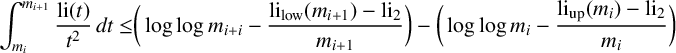 $$ \begin{align*} \int_{m_i}^{m_{i+1}}{\frac{\text{li}(t)}{t^2}}\,dt \leq &\bigg(\log{\log{m_{i+i}}}- \frac{\text{li}_{\text{low}}(m_{i+1}) - \text{li}_2}{m_{i+1}}\bigg) - \bigg(\log{\log{m_{i}}}- \frac{\text{li}_{\text{up}}(m_{i}) - \text{li}_2}{m_{i}}\bigg) \end{align*} $$
$$ \begin{align*} \int_{m_i}^{m_{i+1}}{\frac{\text{li}(t)}{t^2}}\,dt \leq &\bigg(\log{\log{m_{i+i}}}- \frac{\text{li}_{\text{low}}(m_{i+1}) - \text{li}_2}{m_{i+1}}\bigg) - \bigg(\log{\log{m_{i}}}- \frac{\text{li}_{\text{up}}(m_{i}) - \text{li}_2}{m_{i}}\bigg) \end{align*} $$
and finally,
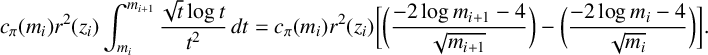 $$ \begin{align*} c_\pi(m_i)r^2(z_i)\int_{m_i}^{m_{i+1}}{\frac{ \sqrt{t}\log{t}}{t^2}}\,dt = c_\pi(m_i)r^2(z_i) \bigg[\bigg( \frac{-2\log{m_{i+1}}-4}{\sqrt{m_{i+1}}} \bigg) - \bigg( \frac{-2\log{m_i}-4}{\sqrt{m_i}} \bigg)\bigg]. \end{align*} $$
$$ \begin{align*} c_\pi(m_i)r^2(z_i)\int_{m_i}^{m_{i+1}}{\frac{ \sqrt{t}\log{t}}{t^2}}\,dt = c_\pi(m_i)r^2(z_i) \bigg[\bigg( \frac{-2\log{m_{i+1}}-4}{\sqrt{m_{i+1}}} \bigg) - \bigg( \frac{-2\log{m_i}-4}{\sqrt{m_i}} \bigg)\bigg]. \end{align*} $$
Combining the above equations gives the desired result.
Lemma 3.2. We have
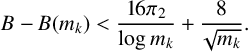 $$ \begin{align} B - B(m_k) < \frac{16 \pi_2}{\log{m_k}} + \frac{8}{\sqrt{m_k}}. \end{align} $$
$$ \begin{align} B - B(m_k) < \frac{16 \pi_2}{\log{m_k}} + \frac{8}{\sqrt{m_k}}. \end{align} $$
Proof. We use [Reference Platt, Trudgian, Bailey, Borwein, Brent, Burachik, Osborn, Sims and Zhu11, Lemma 3] to bound the tail end of B, so that
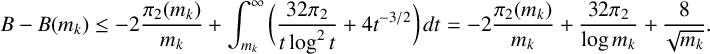 $$ \begin{align*} B - B(m_k) \leq -2 \frac{\pi_2(m_k)}{m_k} + \int_{m_k}^{\infty}{\bigg(\frac{32 \pi_2}{t\log^2{t}} + 4t^{-{3}/{2}}\bigg)\,dt}=-2 \frac{\pi_2(m_k)}{m_k} +\frac{32 \pi_2}{\log{m_k}} + \frac{8}{\sqrt{m_k}}. \end{align*} $$
$$ \begin{align*} B - B(m_k) \leq -2 \frac{\pi_2(m_k)}{m_k} + \int_{m_k}^{\infty}{\bigg(\frac{32 \pi_2}{t\log^2{t}} + 4t^{-{3}/{2}}\bigg)\,dt}=-2 \frac{\pi_2(m_k)}{m_k} +\frac{32 \pi_2}{\log{m_k}} + \frac{8}{\sqrt{m_k}}. \end{align*} $$
Combining the above two lemmas with [Reference Platt, Trudgian, Bailey, Borwein, Brent, Burachik, Osborn, Sims and Zhu11, Lemma 6] gives the following result.
Theorem 3.3. We have
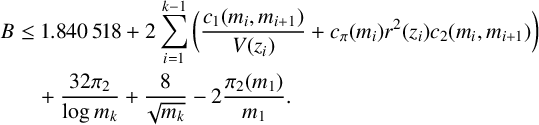 $$ \begin{align*} B &\leq 1.840\,518 + 2 \sum_{i=1}^{k-1}\bigg(\frac{c_1(m_i,m_{i+1})}{V(z_i)} + c_\pi(m_i)r^2(z_i)c_2(m_i,m_{i+1}) \bigg) \\ &\quad + \frac{32 \pi_2}{\log{m_k}} + \frac{8}{\sqrt{m_k}} -2\frac{\pi_2(m_1)}{m_1}. \end{align*} $$
$$ \begin{align*} B &\leq 1.840\,518 + 2 \sum_{i=1}^{k-1}\bigg(\frac{c_1(m_i,m_{i+1})}{V(z_i)} + c_\pi(m_i)r^2(z_i)c_2(m_i,m_{i+1}) \bigg) \\ &\quad + \frac{32 \pi_2}{\log{m_k}} + \frac{8}{\sqrt{m_k}} -2\frac{\pi_2(m_1)}{m_1}. \end{align*} $$
4 Calculating B
The final step is to determine the optimal parameters for the theorem. This involves selecting appropriate intervals
![]() $[m_i,m_{i+1}]$
and choosing corresponding values of
$[m_i,m_{i+1}]$
and choosing corresponding values of
![]() $z_i$
for each interval. Generally, increasing the number of intervals reduces the overall error, though with diminishing returns as the interval size decreases. Based on this principle, we set
$z_i$
for each interval. Generally, increasing the number of intervals reduces the overall error, though with diminishing returns as the interval size decreases. Based on this principle, we set
![]() $m_i \in \{4 \cdot 10^{18}\} \cup \{10^i: i = 19, 19.2, \ldots , 1999.8, 2000\}$
. To determine
$m_i \in \{4 \cdot 10^{18}\} \cup \{10^i: i = 19, 19.2, \ldots , 1999.8, 2000\}$
. To determine
![]() $z_i$
, we employ the Optim package in Julia [Reference Mogensen and Riseth8] to optimise
$z_i$
, we employ the Optim package in Julia [Reference Mogensen and Riseth8] to optimise
![]() $z_i$
within a specified domain. Since the optimal value of
$z_i$
within a specified domain. Since the optimal value of
![]() $z_i$
increases with i, we can restrict the search domain accordingly. Finally, all of the computations for B were performed using the IntervalArithmetic package in Julia [Reference Sanders and Benet12], ensuring rigorous explicit bounds.
$z_i$
increases with i, we can restrict the search domain accordingly. Finally, all of the computations for B were performed using the IntervalArithmetic package in Julia [Reference Sanders and Benet12], ensuring rigorous explicit bounds.
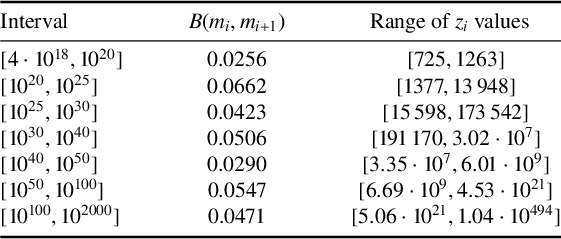
A subset of the optimised parameter ranges is presented in Table 1. The full set of intermediate calculations, along with the optimised values of
![]() $z_i$
for each interval, is available in the linked GitHub repository (https://github.com/LachlanJDunn/B_Under_GRH). This repository also includes the functions used to compute B and perform the parameter sweep. Additionally, it provides a method for estimating bounds on
$z_i$
for each interval, is available in the linked GitHub repository (https://github.com/LachlanJDunn/B_Under_GRH). This repository also includes the functions used to compute B and perform the parameter sweep. Additionally, it provides a method for estimating bounds on
![]() $B(a,b)$
for
$B(a,b)$
for
![]() $4\cdot 10^{18} \leq m_1 \leq a < b \leq m_k$
, by computing
$4\cdot 10^{18} \leq m_1 \leq a < b \leq m_k$
, by computing
![]() $B(m_i,m_j)$
for the smallest interval that fully contains
$B(m_i,m_j)$
for the smallest interval that fully contains
![]() $[a,b]$
.
$[a,b]$
.
Table 1
![]() $B(m_i,m_{i+1})$
for chosen intervals (rounded to 4 significant figures).
$B(m_i,m_{i+1})$
for chosen intervals (rounded to 4 significant figures).
5 Potential improvements
We conclude by discussing several potential improvements to the presented method of bounding B.
-
• As discussed earlier, splicing together different bounds for B over disjoint intervals could provide stronger estimates than restricting to only one method. The intermediate sums computed in this paper have been made available to facilitate this.
-
• Computing
 $B(x_0)$
for a larger
$B(x_0)$
for a larger
 $x_0$
would reduce approximation errors, leading to a more precise bound.
$x_0$
would reduce approximation errors, leading to a more precise bound. -
• Refining the choices of parameters
 $\{m_i\}$
and
$\{m_i\}$
and
 $\{z_i\}$
could potentially yield a more accurate result.
$\{z_i\}$
could potentially yield a more accurate result.
Acknowledgements
This work was completed during and funded by the School of Mathematics and Physics Summer Research program at the University of Queensland. I would like to thank Adrian Dudek for supervising me throughout the program and for all his help during and after the program ended. I would also like to thank Daniel Johnston and Dave Platt for their very helpful discussions and the referee for helpful comments.