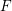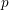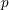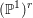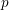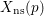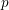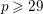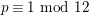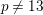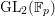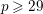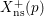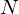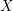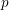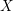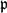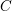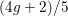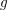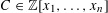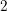Refine listing
Actions for selected content:
355 results in 14Gxx
On Goren–Oort stratification for quaternionic Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2134-2220
- Print publication:
- October 2016
-
- Article
- Export citation
Modular embeddings of Teichmüller curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2269-2349
- Print publication:
- November 2016
-
- Article
- Export citation
ON THE AUTOMORPHISMS OF THE NONSPLIT CARTAN MODULAR CURVES OF PRIME LEVEL
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 09 September 2016, pp. 74-92
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
Computing canonical heights on elliptic curves in quasi-linear time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 391-405
-
- Article
-
- You have access
- Export citation
Character theory approach to Sato–Tate groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 301-314
-
- Article
-
- You have access
- Export citation
Real multiplication through explicit correspondences
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 29-42
-
- Article
-
- You have access
- Export citation
Computing
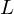 $L$ -series of geometrically hyperelliptic curvesof genus three
$L$ -series of geometrically hyperelliptic curvesof genus three
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 220-234
-
- Article
-
- You have access
- Export citation
A higher-dimensional generalization of Lichtenbaum duality in terms of the Albanese map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1915-1934
- Print publication:
- September 2016
-
- Article
- Export citation
COMPUTING L-FUNCTIONS AND SEMISTABLE REDUCTION OF SUPERELLIPTIC CURVES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 77-108
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
TWISTED GALOIS STRATIFICATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 1-60
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
Failures of weak approximation in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1435-1475
- Print publication:
- July 2016
-
- Article
- Export citation
 $L$ -INDISTINGUISHABILITY ON EIGENVARIETIES
$L$ -INDISTINGUISHABILITY ON EIGENVARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 22 March 2016, pp. 425-440
- Print publication:
- April 2018
-
- Article
- Export citation
GENERALIZED EXPLICIT DESCENT AND ITS APPLICATION TO CURVES OF GENUS 3
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, e6
-
- Article
-
- You have access
- Open access
- Export citation
On the Oort conjecture for Shimura varieties of unitary and orthogonal types
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 889-917
- Print publication:
- May 2016
-
- Article
- Export citation
RATIONAL POINTS ON CUBIC HYPERSURFACES THAT SPLIT INTO FOUR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 29 January 2016, pp. 430-440
- Print publication:
- 2016
-
- Article
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
- Print publication:
- 2016
-
- Article
- Export citation
Strict supports of canonical measures and applications to the geometric Bogomolov conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 997-1040
- Print publication:
- May 2016
-
- Article
- Export citation
ON THE SQUARE-FREE REPRESENTATION FUNCTION OF A NORM FORM AND NILSEQUENCES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 11 November 2015, pp. 107-135
- Print publication:
- February 2018
-
- Article
- Export citation
CERTAIN GENERALIZED MORDELL CURVES OVER THE RATIONAL NUMBERS ARE POINTLESS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 42-64
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Simply connected varieties in characteristic
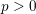 $p>0$
$p>0$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 09 October 2015, pp. 255-287
- Print publication:
- February 2016
-
- Article
- Export citation