Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Helm, David
Tian, Yichao
and
Xiao, Liang
2017.
Tate cycles on some unitary Shimura varieties
mod p.
Algebra & Number Theory,
Vol. 11,
Issue. 10,
p.
2213.
Diamond, Fred
and
Kassaei, Payman L
2017.
Minimal weights of Hilbert modular forms in characteristic .
Compositio Mathematica,
Vol. 153,
Issue. 9,
p.
1769.
EMERTON, MATTHEW
REDUZZI, DAVIDE
and
XIAO, LIANG
2017.
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ARISING FROM HILBERT MODULAR SURFACES.
Forum of Mathematics, Sigma,
Vol. 5,
Issue. ,
Shen, Xu
2019.
ON THE COHOMOLOGY OF SOME SIMPLE SHIMURA VARIETIES WITH BAD REDUCTION.
Journal of the Institute of Mathematics of Jussieu,
Vol. 18,
Issue. 1,
p.
1.
Görtz, Ulrich
He, Xuhua
and
Nie, Sian
2019.
Fully Hodge–Newton Decomposable Shimura Varieties.
Peking Mathematical Journal,
Vol. 2,
Issue. 2,
p.
99.
Tian, Yichao
and
Xiao, Liang
2019.
Tate cycles on some quaternionic Shimura varieties mod p.
Duke Mathematical Journal,
Vol. 168,
Issue. 9,
Liu, Yifeng
and
Tian, Yichao
2020.
Supersingular locus of Hilbert modular varieties, arithmetic level raising and Selmer groups.
Algebra & Number Theory,
Vol. 14,
Issue. 8,
p.
2059.
Dembélé, Lassina
2020.
An intriguing hyperelliptic Shimura curve quotient of genus 16.
Algebra & Number Theory,
Vol. 14,
Issue. 10,
p.
2713.
Diamond, Fred
and
Kassaei, Payman L
2023.
The Cone of Minimal Weights for Mod p Hilbert Modular Forms.
International Mathematics Research Notices,
Vol. 2023,
Issue. 14,
p.
12148.
Caraiani, Ana
and
Tamiozzo, Matteo
2023.
On the étale cohomology of Hilbert modular varieties with torsion coefficients.
Compositio Mathematica,
Vol. 159,
Issue. 11,
p.
2279.
Görtz, Ulrich
He, Xuhua
and
Nie, Sian
2024.
Basic loci of Coxeter type with arbitrary parahoric level.
Canadian Journal of Mathematics,
Vol. 76,
Issue. 1,
p.
126.
Loeffler, David
and
Zerbes, Sarah Livia
2025.
Plectic structures in p-adic de Rham cohomology.
Journal of Number Theory,
Vol. 270,
Issue. ,
p.
238.
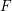 $F$ be a totally real field in which a prime
$F$ be a totally real field in which a prime 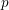 $p$ is unramified. We define the Goren–Oort stratification of the characteristic-
$p$ is unramified. We define the Goren–Oort stratification of the characteristic- 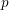 $p$ fiber of a quaternionic Shimura variety of maximal level at
$p$ fiber of a quaternionic Shimura variety of maximal level at 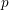 $p$ . We show that each stratum is a
$p$ . We show that each stratum is a 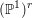 $(\mathbb{P}^{1})^{r}$ -bundle over other quaternionic Shimura varieties (for an appropriate integer
$(\mathbb{P}^{1})^{r}$ -bundle over other quaternionic Shimura varieties (for an appropriate integer  $r$ ). As an application, we give a necessary condition for the ampleness of a modular line bundle on a quaternionic Shimura variety in characteristic
$r$ ). As an application, we give a necessary condition for the ampleness of a modular line bundle on a quaternionic Shimura variety in characteristic 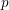 $p$ .
$p$ .