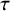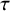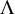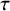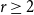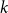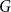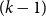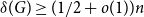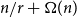Refine listing
Actions for selected content:
1006 results in 05Cxx
Contiguity and remote contiguity of some random graphs
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-18
-
- Article
- Export citation
Graphes dans les surfaces et ergodicité topologique
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-42
-
- Article
- Export citation
Embedding nearly spanning trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-5
-
- Article
- Export citation
A stability theorem for multi-partite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-27
-
- Article
- Export citation
A conditional lower bound for the Turán number of spheres
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modified ascent sequences avoiding a pattern of length 4
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-29
-
- Article
- Export citation
MEASURABLE DOMATIC PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-25
-
- Article
- Export citation
Online matching for the multiclass stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-22
-
- Article
- Export citation
Mutation graph of support
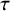 $\tau $-tilting modules over a skew-gentle algebra
$\tau $-tilting modules over a skew-gentle algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Ceresa period from tropical homology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting independent sets in structured graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THREE ALGORITHMIC APPROACHES TO THE GENERAL POSITION PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-9
-
- Article
- Export citation
NONASSORTATIVE COMMUNITY STRUCTURES IN COMPLEX NETWORKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
A large deviation principle for block models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-74
-
- Article
- Export citation
Common pairs of graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-22
-
- Article
- Export citation
On the size of temporal cliques in subcritical random temporal graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 26 June 2025, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
Splines on Cayley graphs of the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 June 2025, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical scaling profile for trees and connected subgraphs on the complete graph
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tight Hamilton cycles with high discrepancy
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 30 May 2025, pp. 565-584
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit laws for the generalized Zagreb indices of random graphs
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 26 May 2025, pp. 1-20
-
- Article
- Export citation