Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Loeffler, David
and
Zerbes, Sarah Livia
2016.
Rankin–Eisenstein classes in Coleman families.
Research in the Mathematical Sciences,
Vol. 3,
Issue. 1,
Andreatta, Fabrizio
Iovita, Adrian
and
Stevens, Glenn
2016.
A 0.5 (half) overconvergent Eichler-Shimura isomorphism.
Annales mathématiques du Québec,
Vol. 40,
Issue. 1,
p.
121.
Greenberg, Matthew
and
Seveso, Marco Adamo
2016.
p-adic families of modular forms and p-adic Abel-Jacobi maps.
Annales mathématiques du Québec,
Vol. 40,
Issue. 2,
p.
397.
Salazar, Daniel Barrera
and
Gao, Shan
2017.
Overconvergent Eichler–Shimura isomorphisms for quaternionic modular forms over ℚ.
International Journal of Number Theory,
Vol. 13,
Issue. 10,
p.
2687.
Saha, Jyoti Prakash
2017.
Purity for families of Galois representations.
Annales de l'Institut Fourier,
Vol. 67,
Issue. 2,
p.
879.
Makiyama, Kenji
2017.
A p-adic analytic family of the D-th Shintani lifting for a Coleman family and congruences between the central L-values.
Journal of Number Theory,
Vol. 181,
Issue. ,
p.
164.
Vonk, Jan
2018.
Modular eigenforms at the boundary of weight space.
Research in Number Theory,
Vol. 4,
Issue. 2,
Greenberg, Matthew
and
Seveso, Marco Adamo
2020.
Triple product p-adic L-functions for balanced weights.
Mathematische Annalen,
Vol. 376,
Issue. 1-2,
p.
103.
Wang, Shan Wen
2021.
Le Système d’Euler de Kato en Famillie (II).
Acta Mathematica Sinica, English Series,
Vol. 37,
Issue. 1,
p.
173.
Jetchev, Dimitar
Loeffler, David
and
Zerbes, Sarah Livia
2021.
Heegner points in Coleman families.
Proceedings of the London Mathematical Society,
Vol. 122,
Issue. 1,
p.
124.
Barrera, Daniel
and
Gao, Shan
2021.
Overconvergent Eichler-Shimura isomorphisms for unitary Shimura curves over totally real fields.
Israel Journal of Mathematics,
Vol. 242,
Issue. 2,
p.
707.
Barrera Salazar, Daniel
and
Williams, Chris
2022.
Overconvergent cohomology, p-adic L-functions and families for GL(2) over CM fields.
Journal de théorie des nombres de Bordeaux,
Vol. 33,
Issue. 3.1,
p.
659.
Bertolini, Massimo
Darmon, Henri
and
Venerucci, Rodolfo
2022.
Heegner points and Beilinson–Kato elements: A conjecture of Perrin-Riou.
Advances in Mathematics,
Vol. 398,
Issue. ,
p.
108172.
Benois, Denis
and
Büyükboduk, Kâzım
2022.
Interpolation of Beilinson–Kato elements and p-adic L-functions.
Annales mathématiques du Québec,
Vol. 46,
Issue. 2,
p.
231.
Rodríguez Camargo, Juan Esteban
2023.
p-adic Eichler–Shimura maps for the modular curve.
Compositio Mathematica,
Vol. 159,
Issue. 6,
p.
1214.
Loeffler, David
and
Rivero Salgado, Oscar
2024.
Eisenstein degeneration of Euler systems.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2024,
Issue. 814,
p.
241.
Andreatta, Fabrizio
and
Iovita, Adrian
2024.
OVERCONVERGENT DE RHAM EICHLER–SHIMURA MORPHISMS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 23,
Issue. 2,
p.
647.
Nuccio Mortarino Majno di Capriglio, Filippo Alberto Edoardo
Ochiai, Tadashi
and
Ray, Jishnu
2024.
A formal model of Coleman families and applications to Iwasawa invariants.
Annales mathématiques du Québec,
Vol. 48,
Issue. 2,
p.
453.
Benois, D.
and
Horte, S.
2024.
On extra zeros of 𝑝-adic Rankin–Selberg 𝐿-functions.
St. Petersburg Mathematical Journal,
Vol. 34,
Issue. 6,
p.
929.
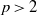 $p\gt 2$ , an integer
$p\gt 2$ , an integer 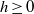 $h\geq 0$ , and a wide open disk
$h\geq 0$ , and a wide open disk 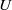 $U$ in the weight space
$U$ in the weight space 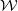 $ \mathcal{W} $ of
$ \mathcal{W} $ of 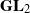 ${\mathbf{GL} }_{2} $ , we construct a Hecke–Galois-equivariant morphism
${\mathbf{GL} }_{2} $ , we construct a Hecke–Galois-equivariant morphism 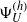 ${ \Psi }_{U}^{(h)} $ from the space of analytic families of overconvergent modular symbols over
${ \Psi }_{U}^{(h)} $ from the space of analytic families of overconvergent modular symbols over 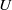 $U$ with bounded slope
$U$ with bounded slope 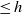 $\leq h$ , to the corresponding space of analytic families of overconvergent modular forms, all with
$\leq h$ , to the corresponding space of analytic families of overconvergent modular forms, all with 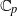 ${ \mathbb{C} }_{p} $ -coefficients. We show that there is a finite subset
${ \mathbb{C} }_{p} $ -coefficients. We show that there is a finite subset 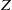 $Z$ of
$Z$ of 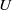 $U$ for which this morphism induces a
$U$ for which this morphism induces a 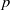 $p$ -adic analytic family of isomorphisms relating overconvergent modular symbols of weight
$p$ -adic analytic family of isomorphisms relating overconvergent modular symbols of weight 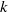 $k$ and slope
$k$ and slope 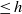 $\leq h$ to overconvergent modular forms of weight
$\leq h$ to overconvergent modular forms of weight 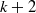 $k+ 2$ and slope
$k+ 2$ and slope 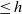 $\leq h$ .
$\leq h$ .
