Hostname: page-component-784d4fb959-nsmbk Total loading time: 0 Render date: 2025-07-14T17:48:52.716Z Has data issue: false hasContentIssue false
  • English
  • Français

The Chabauty–Coleman bound at a prime of bad reduction and Clifford bounds for geometric rank functions

Part of: Arithmetic problems. Diophantine geometry Graph theory

Published online by Cambridge University Press:  09 October 2013

Eric Katz  and
David Zureick-Brown
Eric Katz
Affiliation:
Department of Combinatorics & Optimization, University of Waterloo, 200 University Avenue West, Waterloo, ON, Canada N2L 3G1 email eekatz@math.uwaterloo.ca
David Zureick-Brown
Affiliation:
Department of Mathematics and Computer science, Emory University, Atlanta, GA 30322, USA email dzb@mathcs.emory.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 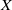$X$ be a curve over a number field 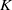$K$ with genus 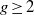$g\geq 2$, 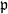$\mathfrak{p}$ a prime of 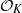${ \mathcal{O} }_{K} $ over an unramified rational prime 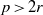$p\gt 2r$, 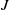$J$ the Jacobian of 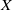$X$, 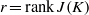$r= \mathrm{rank} \hspace{0.167em} J(K)$, and 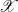$\mathscr{X}$ a regular proper model of 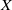$X$ at 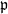$\mathfrak{p}$. Suppose 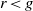$r\lt g$. We prove that 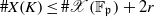$\# X(K)\leq \# \mathscr{X}({ \mathbb{F} }_{\mathfrak{p}} )+ 2r$, extending the refined version of the Chabauty–Coleman bound to the case of bad reduction. The new technical insight is to isolate variants of the classical rank of a divisor on a curve which are better suited for singular curves and which satisfy Clifford’s theorem.

Keywords

Chabautychip firingtropical geometry

MSC classification

Secondary: 14G05: Rational points 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 14T05: Tropical geometry

Information

Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 11 , November 2013 , pp. 1818 - 1838
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amini, O. and Baker, M., Linear series on metrized complexes of algebraic curves, Preprint (2012).Google Scholar
Amini, O. and Caporaso, L., Riemann–Roch theory for weighted graphs and tropical curves, Preprint (2011), arXiv:1112.5134[math.CO].Google Scholar
Baker, M., Specialization of linear systems from curves to graphs, Algebra Number Theory 2 (2008), 613–653, with an appendix by Brian Conrad, doi:10.2140/ant.2008.2.613; MR 2448666(2010a:14012).CrossRefGoogle Scholar
Baker, M. and Norine, S., Riemann–Roch and Abel–Jacobi theory on a finite graph, Adv. Math. 215 (2007), 766–788; MR 2355607(2008m:05167).Google Scholar
Bombieri, E., The Mordell conjecture revisited, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 17 (1990), 615–640; MR 1093712(92a:11072).Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer, Berlin, 1990); MR 1045822(91i:14034).Google Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), 235–265; Computational algebra and number theory (London, 1993). Magma is available at http://magma.maths.usyd.edu.au/magma/; MR 1484478.CrossRefGoogle Scholar
Bruin, N., The Diophantine equations ${x}^{2} \pm {y}^{4} = \pm {z}^{6} $ and ${x}^{2} + {y}^{8} = {z}^{3} $, Compositio Math. 118 (1999), 305–321; MR 1711307(2001d:11035).CrossRefGoogle Scholar
Bruin, N. and Stoll, M., Deciding existence of rational points on curves: an experiment, Experiment. Math. 2 (2008), 181–189; MR 2433884(2009d:11100).CrossRefGoogle Scholar
Bruin, N. and Stoll, M., The Mordell–Weil sieve: proving non-existence of rational points on curves, LMS J. Comput. Math. 13 (2010), 272–306, doi:10.1112/S1461157009000187; MR 2685127(2011j:11118).Google Scholar
Chabauty, C., Sur les points rationnels des courbes algébriques de genre supérieur à l’unité, C. R. Acad. Sci. Paris 212 (1941), 882–885 (in French); MR 0004484(3,14d).Google Scholar
Coleman, R. F., Effective Chabauty, Duke Math. J. 52 (1985), 765–770; MR 808103(87f:11043).Google Scholar
Faltings, G., Finiteness theorems for Abelian varieties over number fields, in Arithmetic geometry (Storrs, Conn., 1984) (Springer, New York, 1986), 9–27, Translated from the German original [Invent. Math. 73 (1983), 349–366; Invent. Math. 75 (1984), 381; MR 85g:11026ab] by E. Shipz; MR 861971.Google Scholar
Grant, D., A curve for which Coleman’s effective Chabauty bound is sharp, Proc. Amer. Math. Soc. 122 (1994), 317–319; MR 1242084(94k:14019).Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977); MR 0463157(57 #3116).Google Scholar
Liu, Q., Algebraic geometry and arithmetic curves, Oxford Graduate Texts in Mathematics, vol. 6 (Oxford University Press, Oxford, 2006), Translated from the French by Reinie Erné; Oxford Science Publications.Google Scholar
Lorenzini, D. J., Dual graphs of degenerating curves, Math. Ann. 287 (1990), 135–150, doi:10.1007/BF01446881;  MR 1048284(91j:14018).CrossRefGoogle Scholar
Lorenzini, D. J., Two-variable zeta-functions on graphs and Riemann–Roch theorems, Int. Math. Res. Not. 2012 (2012), 5100–5131; doi:10.1093/imrn/rnr227.CrossRefGoogle Scholar
Lorenzini, D. J. and Tucker, T. J., Thue equations and the method of Chabauty–Coleman, Invent. Math. 148 (2002), 47–77; MR 1892843(2003d:11088).CrossRefGoogle Scholar
McCallum, W. and Poonen, B., The method of Chabauty and Coleman, Preprint (2010), http://www-math.mit.edu/~poonen/papers/chabauty.pdf, Panoramas et Synthèses, Société Math. de France, to appear.Google Scholar
Poonen, B., Computing rational points on curves, in Number theory for the millennium, III (Urbana, IL, 2000) (A K Peters, Natick, MA, 2002), 149–172; MR 1956273(2003k:11105).Google Scholar
Poonen, B. and Schaefer, E. F., Explicit descent for Jacobians of cyclic covers of the projective line, J. Reine Angew. Math. 488 (1997), 141–188; MR 1465369(98k:11087).Google Scholar
Poonen, B., Schaefer, E. F. and Stoll, M., Twists of $X(7)$ and primitive solutions to ${x}^{2} + {y}^{3} = {z}^{7} $, Duke Math. J. 137 (2007), 103–158; MR 2309145.Google Scholar
Skolem, Th., Ein Verfahren zur Behandlung gewisser exponentialer Gleichungen und diophantischer Gleichungen, 8. Scand. Mat. Kongr. (1934), 163–169.Google Scholar
Stoll, M., Independence of rational points on twists of a given curve, Compositio Math. 142 (2006), 1201–1214; MR 2264661.Google Scholar
Stoll, M., Rational 6-cycles under iteration of quadratic polynomials, LMS J. Comput. Math. 11 (2008), 367–380, doi:10.1112/S1461157000000644;  MR 2465796 (2010b:11067).CrossRefGoogle Scholar
Stoll, M., Rational points on curves, J. Théor. Nombres Bordeaux 23 (2011), 257–277; (English, with English and French summaries); MR 2780629(2012d:14037).Google Scholar
Vojta, P., Siegel’s theorem in the compact case, Ann. of Math. (2) 133 (1991), 509–548; MR 1109352 (93d:11065).Google Scholar