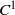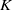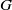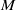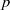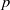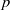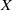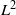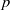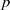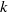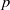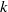Contents
Research Article
A robustly chain transitive attractor with singularities of different indices
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2012, pp. 449-501
-
- Article
- Export citation
Box splines and the equivariant index theorem
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2012, pp. 503-544
-
- Article
- Export citation
Descent obstructions and Brauer–Manin obstruction in positive characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2012, pp. 545-551
-
- Article
- Export citation
New global stability estimates for the Calderón problem in two dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2012, pp. 553-569
-
- Article
- Export citation
Boundary behaviour of special cohomology classes arising from the Weil representation
- Part of:
-
- Published online by Cambridge University Press:
- 03 July 2012, pp. 571-634
-
- Article
- Export citation
Improved local energy decay for the wave equation on asymptotically Euclidean odd dimensional manifolds in the short range case
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2012, pp. 635-650
-
- Article
- Export citation
Random Dieudonné modules, random
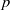 $p$-divisible groups, and random curves over finite fields
$p$-divisible groups, and random curves over finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2013, pp. 651-676
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 12 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 21 May 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
JMJ volume 12 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 21 May 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation