Refine listing
Actions for selected content:
292 results in 47Axx
Quantitative ergodic theorems for actions of groups of polynomial growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-54
-
- Article
- Export citation
Evans function, parity and nonautonomous bifurcations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher-order trace formulas for contractive and dissipative operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-26
-
- Article
- Export citation
On Bauschke–Bendit–Moursi modulus of averagedness and classifications of averaged nonexpansive operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Kakutani–Rokhlin decomposition for conditionally ergodic process in the measure-free setting of vector lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 05 August 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Airy operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-31
-
- Article
- Export citation
On weaving Hilbert space frames and Riesz bases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 July 2025, pp. 1-10
-
- Article
- Export citation
Density properties of orbits for a hypercyclic operator on a Banach space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 18 July 2025, pp. 1-16
-
- Article
- Export citation
The Schur–Agler class in infinitely many variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
At the crossroads of holomorphic dynamic and operator theory: spectral properties of composition operators on
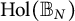 $\mathrm {Hol}(\mathbb {B}_N)$
$\mathrm {Hol}(\mathbb {B}_N)$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-26
-
- Article
- Export citation
Hereditarily frequently hypercyclic operators and disjoint frequent hypercyclicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 3021-3072
- Print publication:
- October 2025
-
- Article
- Export citation
Zero-one law of orbital limit points for weighted shifts
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 945-978
-
- Article
- Export citation
Generalized Knill–Laflamme theorem for families of isoclinic subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 992-1010
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic Muckenhoupt weights characterized by parabolic fractional maximal and integral operators with time lag
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1-54
-
- Article
- Export citation
Isometric dilation and Sarason’s commutant lifting theorem in several variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1-33
-
- Article
- Export citation
On a general matrix-valued unbalanced optimal transport problem
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On commutators of square-zero Hilbert space operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-36
-
- Article
- Export citation
The algebraic numerical range as a spectral set in Banach algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON RESTRICTED BOUNDARIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 334-344
- Print publication:
- October 2025
-
- Article
- Export citation
Absolute dilations of UCP self-adjoint Fourier multipliers: the nonunimodular case
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 307-324
- Print publication:
- September 2025
-
- Article
- Export citation




















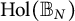




















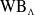
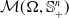
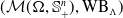
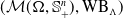

 . When
. When 
 and its norm-closure
and its norm-closure  . In the infinite-dimensional setting, we characterise the intersection of
. In the infinite-dimensional setting, we characterise the intersection of  with the set of biquasitriangular operators, and we exhibit an index obstruction to belonging to
with the set of biquasitriangular operators, and we exhibit an index obstruction to belonging to  .
.







































