Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-11T03:13:11.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Sato–Tate distributions and Galois endomorphism modules in genus 2

Part of: Arithmetic algebraic geometry Zeta and $L$-functions: analytic theory Abelian varieties and schemes Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  25 July 2012

Francesc Fité ,
Kiran S. Kedlaya ,
Víctor Rotger  and
Andrew V. Sutherland
Francesc Fité
Affiliation:
Department of Mathematics, Universität Bielefeld, Postfach 100131, D-33501 Bielefeld, Germany (email: francesc.fite@gmail.com)
Kiran S. Kedlaya
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA (email: kedlaya@mit.edu, kedlaya@ucsd.edu)
Víctor Rotger
Affiliation:
Departament Matemàtica Aplicada II, Universitat Politècnica de Catalunya, Campus Nord, Edifici Omega, Despatx 413, Jordi Girona, 1-3, 08034 Barcelona, Spain (email: victor.rotger@upc.edu)
Andrew V. Sutherland
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA (email: drew@math.mit.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an abelian surface A over a number field k, we study the limiting distribution of the normalized Euler factors of the L-function of A. This distribution is expected to correspond to taking characteristic polynomials of a uniform random matrix in some closed subgroup of USp(4); this Sato–Tate group may be obtained from the Galois action on any Tate module of A. We show that the Sato–Tate group is limited to a particular list of 55 groups up to conjugacy. 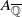We then classify A according to the Galois module structure on the ℝ-algebra generated by endomorphisms of (the Galois type), and establish a matching with the classification of Sato–Tate groups; this shows that there are at most 52 groups up to conjugacy which occur as Sato–Tate groups for suitable A and k, of which 34 can occur for k=ℚ. Finally, we present examples of Jacobians of hyperelliptic curves exhibiting each Galois type (over ℚ whenever possible), and observe numerical agreement with the expected Sato–Tate distribution by comparing moment statistics.

Keywords

Sato–Tate distributionsabelian surfacesendomorphism algebrasGalois type

MSC classification

Secondary: 11M50: Relations with random matrices 11G10: Abelian varieties of dimension $> 1$ 11G20: Curves over finite and local fields 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture) 14K15: Arithmetic ground fields
Type
Research Article
Information
Compositio Mathematica , Volume 148 , Issue 5 , September 2012 , pp. 1390 - 1442
Copyright
Copyright © Foundation Compositio Mathematica 2012

References

[BK11]Banaszak, G. and Kedlaya, K. S., An algebraic Sato–Tate group and Sato–Tate conjecture, Preprint (2011), arXiv:1109.4449v1.Google Scholar
[BGG11]Barnet-Lamb, T., Geraghty, D. and Gee, T., The Sato–Tate conjecture for Hilbert modular forms, J. Amer. Math. Soc. 24 (2011), 411–469.CrossRefGoogle Scholar
[BGHT11]Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi–Yau varieties and potential automorphy II, Publ. Res. Inst. Math. Sci. 47 (2011), 29–98.CrossRefGoogle Scholar
[Bea10]Beauville, A., Finite subgroups of PGL2(K), Contemporary Mathematics, vol. 522 (American Mathematical Society, Providence, RI, 2010).Google Scholar
[Bog80]Bogomolov, F. A., Sur l’algébricité des représentations ℓ-adiques, C. R. Acad. Sci. Paris 290 (1980), 701–703.Google Scholar
[CF00]Chinburg, T. and Friedman, E., The finite subgroups of maximal arithmetic Kleinian groups, Ann. Inst. Fourier Grenoble 50 (2000), 1765–1798.CrossRefGoogle Scholar
[Del82]Deligne, P., Hodge cycles on abelian varieties, in Hodge cycles, motives, and Shimura varieties, Lecture Notes in Mathematics, vol. 900 (Springer, Berlin, 1982), 9–100.CrossRefGoogle Scholar
[Fal83]Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent. Math. 73 (1983), 349–366.CrossRefGoogle Scholar
[Fit10]Fité, F., Artin representations attached to pairs of isogenous abelian varieties, Preprint (2010), arXiv:1012.3390v1.Google Scholar
[GHM08]Galbraith, S. D., Harrison, M. and Mireles Morales, D. J., Efficient hyperelliptic arithmetic using balanced representation for divisors, in Algorithmic number theory: 8th international symposium, ANTS-VIII (Banff, Canada, May 2008) proceedings, Lecture Notes in Computer Science, vol. 5011 (Springer, Berlin, 2008), 342–356.CrossRefGoogle Scholar
[GS01]Gaudry, P. and Schost, É., On the invariants of the quotients of the Jacobian of a curve of genus 2, in Applied algebra, algebraic algorithms and error-correcting codes: 14th international symposium, AAECC-14 (Melbourne, Australia, November 2001) proceedings, Lecture Notes in Computer Science, vol. 2227 (Springer, Berlin, 2001), 373–386.CrossRefGoogle Scholar
[Har09]Harris, M., Potential automorphy of odd-dimensional symmetric powers of elliptic curves, and applications, in Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Volume II, Progress in Mathematics, vol. 270 (Birkhäuser, Boston, MA, 2009), 1–21.Google Scholar
[KS99]Katz, N. M. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy, American Mathematical Society Colloquium Publications, vol. 45 (American Mathematical Society, Providence, RI, 1999).Google Scholar
[KS08]Kedlaya, K. S. and Sutherland, A. V., Computing L-series of hyperelliptic curves, in Algorithmic number theory: 8th international symposium, ANTS-VIII (Banff, Canada, May 2008) proceedings, Lecture Notes in Computer Science, vol. 5011 (Springer, Berlin, 2008), 312–326.CrossRefGoogle Scholar
[KS09]Kedlaya, K. S. and Sutherland, A. V., Hyperelliptic curves, L-polynomials, and random matrices, in Arithmetic, geometry, cryptography, and coding theory: international conference, November 5–9, 2007, CIRM, Marseilles, France, Contemporary Mathematics, vol. 487 (American Mathematical Society, Providence, RI, 2009), 119–162.CrossRefGoogle Scholar
[Mum69]Mumford, D., A note of Shimura’s paper “Discontinuous subgroups and abelian varieties”, Math. Ann. 181 (1969), 345–351.CrossRefGoogle Scholar
[Mum70]Mumford, D., Abelian varieties (Oxford University Press, Oxford, for Tata Institute of Fundamental Research, Bombay, 1970).Google Scholar
[OEIS] The OEIS Foundation Inc., On-Line Encyclopedia of Integer Sequences (OEIS), http://oeis.org.Google Scholar
[Rib04]Ribet, K. A., Abelian varieties over ℚ and modular forms, in Modular curves and abelian varieties, Progress in Mathematics, vol. 224, eds Cremona, J., Lario, J.-C., Quer, J. and Ribet, K. (Birkhäuser, Basel, 2004), 241–261.CrossRefGoogle Scholar
[Ser68]Serre, J.-P., Abelian ℓ-adic representations and elliptic curves (W.A. Benjamin, New York, 1968).Google Scholar
[Ser72]Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15 (1972), 259–331.CrossRefGoogle Scholar
[Se81]Serre, J.-P., Lettres à Ken Ribet du 1/1/1981 et du 29/1/1981, in Œuvres. Collected papers. Volume IV: 1985–1998 (Springer, Berlin, 2000).CrossRefGoogle Scholar
[Ser92]Serre, J.-P., Lie algebras and Lie groups, Lecture Notes in Mathematics, vol. 1500 (Springer, Berlin, 1992).CrossRefGoogle Scholar
[Ser94]Serre, J.-P., Propriétés conjecturales des groupes de Galois motiviques et des représentations l-adiques, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, vol. 55 (American Mathematical Society, Providence, RI, 1994), 377–400.Google Scholar
[Ser12]Serre, J.-P., Lectures on N X(p) (CRC Press, Boca Raton, FL, 2012).Google Scholar
[Shi63]Shimura, G., On analytic families of polarized abelian varieties and automorphic functions, Ann. of Math. (2) 78 (1963), 149–192.CrossRefGoogle Scholar
[Shi71]Shimura, G., On the zeta-function of an abelian variety with complex multiplication, Ann. of Math. (2) 94 (1971), 504–533.CrossRefGoogle Scholar
[Shi98]Shimura, G., Abelian varieties with complex multiplication and modular forms (Princeton University Press, Princeton, NJ, 1998).CrossRefGoogle Scholar
[ST61]Shimura, G. and Taniyama, Y., Complex multiplication of abelian varieties and its application to number theory, Publications of the Mathematical Society of Japan, vol. 6 (Mathematical Society of Japan, Tokyo, 1961).Google Scholar
[Sil92]Silverberg, A., Fields of definition for homomorphisms of abelian varieties, J. Pure Appl. Algebra 77 (1992), 253–262.CrossRefGoogle Scholar
[Sil94]Silverman, J. H., Advanced topics in the arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 151 (Springer, New York, 1994).CrossRefGoogle Scholar
[Ste11]Stein, W. A.et al., Sage mathematics software (version 4.7.1), The Sage Development Team (2011), http://www.sagemath.org.Google Scholar
[Ste65]Steinberg, R., Regular elements of semisimple algebraic groups, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 49–80.CrossRefGoogle Scholar
[Str10]Streng, M., Complex multiplication of abelian surfaces, PhD thesis, Universiteit Leiden (2010).Google Scholar
[Sut07]Sutherland, A. V., Order computations in generic groups, PhD thesis, Massachusetts Institute of Technology (2007).Google Scholar
[Sut11a]Sutherland, A. V., smalljac software library, version 4.0 (2011).Google Scholar
[Sut11b]Sutherland, A. V., Structure computation and discrete logarithms in finite abelian p-groups, Math. Comp. 80 (2011), 477–500.CrossRefGoogle Scholar
[Wei64]Weil, A., Remarks on the cohomology of groups, Ann. of Math. (2) 80 (1964), 149–157.CrossRefGoogle Scholar
[Yos73]Yoshida, H., On an analogue of the Sato conjecture, Invent. Math. 19 (1973), 261–277.CrossRefGoogle Scholar
[Zar00]Zarhin, Yu. G., Hyperelliptic Jacobians without complex multiplication, Math. Res. Lett. 7 (2000), 123–132.CrossRefGoogle Scholar