Refine listing
Actions for selected content:
292 results in 47Axx
OPERATOR QUASILINEARITY OF SOME FUNCTIONALS ASSOCIATED WITH DAVIS–CHOI–JENSEN’S INEQUALITY FOR POSITIVE MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 322-332
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
SOME INEQUALITIES FOR THE NUMERICAL RADIUS FOR HILBERT SPACE OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 489-496
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
ON THE VARIATIONAL CONSTANT ASSOCIATED TO THE
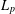 $L_{p}$ -HARDY INEQUALITY
$L_{p}$ -HARDY INEQUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 23 September 2016, pp. 405-419
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
THE STRONG IRREDUCIBILITY OF A CLASS OF COWEN–DOUGLAS OPERATORS ON BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 479-488
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
A SPECTRAL CHARACTERIZATION OF
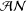 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 369-391
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
More on hypergeometric Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 153-158
- Print publication:
- July 2016
-
- Article
- Export citation
THE CESÀRO OPERATOR IN THE FRÉCHET SPACES ℓp+ AND L p−
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 273-287
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
ON THE FREQUENT UNIVERSALITY OF UNIVERSAL TAYLOR SERIES IN THE COMPLEX PLANE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 109-117
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
SPLITTING INVARIANT SUBSPACES IN THE HARDY SPACE OVER THE BIDISK
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 205-223
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Formulations of the
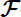 -functional calculus and some consequences
-functional calculus and some consequences
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 05 May 2016, pp. 509-545
- Print publication:
- June 2016
-
- Article
- Export citation
LOCAL DECAY FOR THE DAMPED WAVE EQUATION IN THE ENERGY SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 01 April 2016, pp. 509-540
- Print publication:
- June 2018
-
- Article
- Export citation
Elliptic problems for a Douglis–Nirenberg system over ℝn and over an exterior subregion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 579-594
- Print publication:
- June 2016
-
- Article
- Export citation
POLISH MODELS AND SOFIC ENTROPY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 18 January 2016, pp. 241-275
- Print publication:
- April 2018
-
- Article
- Export citation
On functional calculus properties of Ritt operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 26 November 2015, pp. 1239-1250
- Print publication:
- December 2015
-
- Article
- Export citation
High Order Finite Difference Discretization for Composite Grid Hierarchy and Its Applications
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1211-1233
- Print publication:
- November 2015
-
- Article
- Export citation
SPECTRUM AND COMPACTNESS OF THE CESÀRO OPERATOR ON WEIGHTED
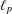 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 287-314
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
STABILITY OF UNCONDITIONAL SCHAUDER DECOMPOSITIONS IN
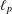 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 August 2015, pp. 444-456
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
EMBEDDING AND TRACE RESULTS FOR VARIABLE EXPONENT SOBOLEV AND MAZ'YA SPACES ON NON-SMOOTH DOMAINS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 471-489
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
LEBESGUE DECOMPOSITION FOR REPRESENTABLE FUNCTIONALS ON *-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 491-501
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
Boundedness of integral operators on decreasing functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 725-744
- Print publication:
- August 2015
-
- Article
- Export citation
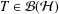
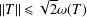
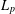
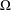
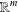
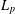
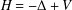
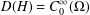
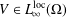
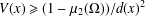
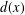
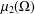
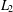
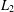
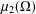
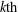
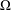
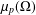
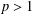
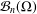

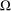
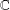
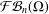
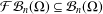
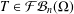
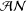
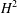
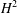
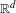
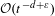
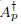 the operator induced in this setting by the problem over ℝ
the operator induced in this setting by the problem over ℝ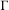
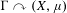
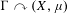
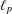
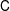
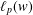
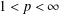
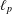

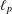
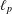
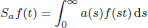
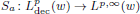 was completely solved, the characterization of the weights
was completely solved, the characterization of the weights 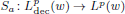 is bounded is still open for the case in which
is bounded is still open for the case in which 