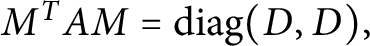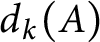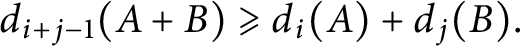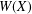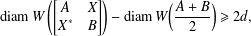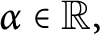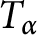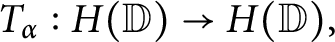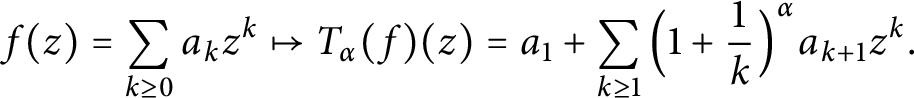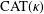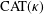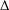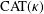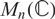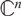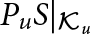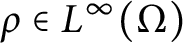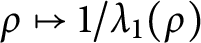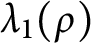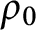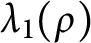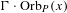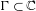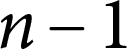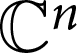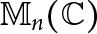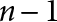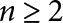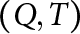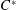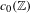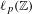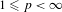Refine listing
Actions for selected content:
292 results in 47Axx
Variational principles for symplectic eigenvalues
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 553-559
- Print publication:
- September 2021
-
- Article
- Export citation
VARIANTS OF ANDO–HIAI TYPE INEQUALITIES FOR DEFORMED MEANS AND APPLICATIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 622-639
- Print publication:
- September 2021
-
- Article
- Export citation
GLOBAL SUBELLIPTIC ESTIMATES FOR KRAMERS–FOKKER–PLANCK OPERATORS WITH SOME CLASS OF POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 675-711
- Print publication:
- March 2022
-
- Article
- Export citation
NUMERICAL RANGE AND POSITIVE BLOCK MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 69-77
- Print publication:
- February 2021
-
- Article
- Export citation
Growth of frequently hypercyclic functions for some weighted Taylor shifts on the unit disc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 264-281
- Print publication:
- June 2021
-
- Article
- Export citation
 $\unicode[STIX]{x1D6E5}$-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN
$\unicode[STIX]{x1D6E5}$-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN 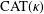 $\text{CAT}(\unicode[STIX]{x1D705})$ SPACES
$\text{CAT}(\unicode[STIX]{x1D705})$ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 289-301
- Print publication:
- June 2021
-
- Article
- Export citation
HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 280-290
- Print publication:
- May 2021
-
- Article
- Export citation
The Dual of the Compressed Shift
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 April 2020, pp. 98-111
- Print publication:
- March 2021
-
- Article
- Export citation
Steiner symmetry in the minimization of the first eigenvalue of a fractional eigenvalue problem with indefinite weight
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 April 2020, pp. 970-992
- Print publication:
- August 2021
-
- Article
- Export citation
Orbits of homogeneous polynomials on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1627-1655
- Print publication:
- June 2021
-
- Article
- Export citation
The Distance from a Rank
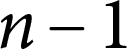 $n-1$ Projection to the Nilpotent Operators on
$n-1$ Projection to the Nilpotent Operators on 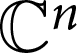 $\mathbb {C}^n$
$\mathbb {C}^n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 02 April 2020, pp. 54-74
- Print publication:
- March 2021
-
- Article
- Export citation
Operators on Anti-dual pairs: Self-adjoint Extensions and the Strong Parrott Theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 813-824
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
Shadowing and structural stability for operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 961-980
- Print publication:
- April 2021
-
- Article
- Export citation
INEQUALITIES OF JENSEN’S TYPE FOR POSITIVE LINEAR FUNCTIONALS ON HERMITIAN UNITAL BANACH
 $\ast$-ALGEBRAS
$\ast$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 308-318
- Print publication:
- October 2020
-
- Article
- Export citation
Frequent universality criterion and densities
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 25 November 2019, pp. 846-868
- Print publication:
- March 2021
-
- Article
- Export citation
Escaping a Neighborhood Along a Prescribed Sequence in Lie Groups and Banach Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 484-505
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
CONTINUITY OF A CONDITION SPECTRUM AND ITS LEVEL SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 09 September 2019, pp. 412-430
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
PACKING SUBORDINACY WITH APPLICATION TO SPECTRAL CONTINUITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 13 June 2019, pp. 226-244
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CONVEXITY OF PARAMETER EXTENSIONS OF SOME RELATIVE OPERATOR ENTROPIES WITH A PERSPECTIVE APPROACH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 737-744
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Simultaneous Upper Triangular Forms for Commuting Operators in a Finite von Neumann Algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 15 May 2019, pp. 1188-1245
- Print publication:
- October 2020
-
- Article
- Export citation