Published online by Cambridge University Press: 24 January 2020
The aim of this paper is to develop an approach to obtain self-adjoint extensions of symmetric operators acting on anti-dual pairs. The main advantage of such a result is that it can be applied for structures not carrying a Hilbert space structure or a normable topology. In fact, we will show how hermitian extensions of linear functionals of involutive algebras can be governed by means of their induced operators. As an operator theoretic application, we provide a direct generalization of Parrott’s theorem on contractive completion of 2 by 2 block operator-valued matrices. To exhibit the applicability in noncommutative integration, we characterize hermitian extendibility of symmetric functionals defined on a left ideal of a 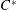 $C^{\ast }$-algebra.
$C^{\ast }$-algebra.
The corresponding author Zs. Tarcsay was supported by DAAD-TEMPUS Cooperation Project “Harmonic Analysis and Extremal Problems” (grant no. 308015). Project no. ED 18-1-2019-0030 (Application-specific highly reliable IT solutions) has been implemented with the support provided from the National Research, Development and Innovation Fund of Hungary, financed under the Thematic Excellence Programme funding scheme.
T. Titkos was supported by the Hungarian National Research, Development and Innovation Office - NKFIH (Grant No. PD128374 and Grant No. K115383), by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences, and by the ÚNKP-18-4-BGE-3 New National Excellence Program of the Ministry of Human Capacities.