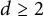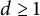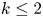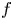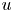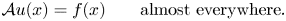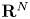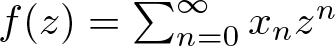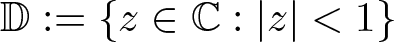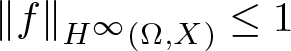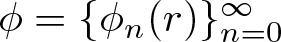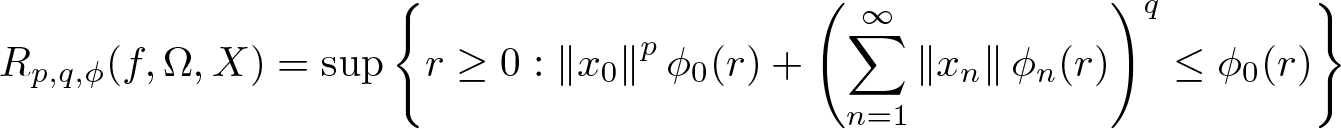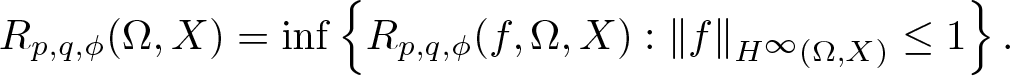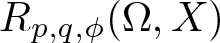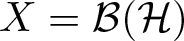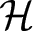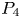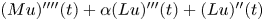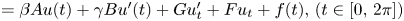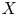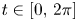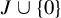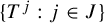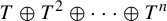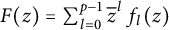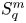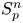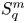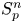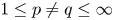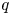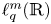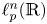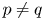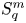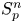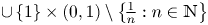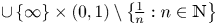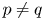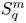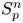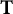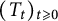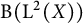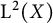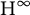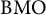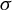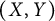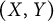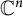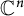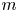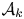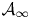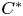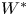Refine listing
Actions for selected content:
292 results in 47Axx
Symmetric and antisymmetric tensor products for the function-theoretic operator theorist
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 324-346
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Norms on complex matrices induced by random vectors II: extension of weakly unitarily invariant norms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 447-457
- Print publication:
- June 2024
-
- Article
- Export citation
A Lebesgue–Lusin property for linear operators of first and second order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 06 November 2023, pp. 858-868
- Print publication:
- June 2025
-
- Article
- Export citation
Bohr radius for Banach spaces on simply connected domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 113-141
-
- Article
- Export citation
Spectral mapping theorems for essential spectra and regularized functional calculi
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 12 October 2023, pp. 634-656
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tensor algebras of subproduct systems and noncommutative function theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1587-1608
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic solutions of four-order degenerate differential equations with finite delay in vector-valued function spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 September 2023, pp. 395-412
- Print publication:
- April 2025
-
- Article
- Export citation
Every symmetric Kubo–Ando connection has the order-determining property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 September 2023, pp. 279-288
- Print publication:
- June 2024
-
- Article
- Export citation
Remarks on countable subadditivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1504-1517
- Print publication:
- October 2024
-
- Article
- Export citation
Disjoint hypercyclicity, Sidon sets and weakly mixing operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1315-1329
- Print publication:
- May 2024
-
- Article
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Bohr operator on operator-valued polyanalytic functions on simply connected domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1411-1422
- Print publication:
- December 2023
-
- Article
- Export citation
On isometric embeddability of $S_q^m$
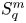 into $S_p^n$
into $S_p^n$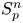 as non-commutative quasi-Banach spaces
as non-commutative quasi-Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 June 2023, pp. 1180-1203
- Print publication:
- August 2024
-
- Article
- Export citation
Nontrivial invariant subspaces of linear operator pencils
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1-8
- Print publication:
- March 2024
-
- Article
- Export citation
THE RESTRICTED CONNECTED HULL: FILLING THE HOLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 April 2023, pp. 388-392
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dilations of Markovian semigroups of measurable Schur multipliers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 774-797
- Print publication:
- June 2024
-
- Article
- Export citation
Pure point spectrum for dynamical systems and mean, Besicovitch and Weyl almost periodicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 524-568
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
General Toeplitz kernels and
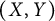 $(X,Y)$-invariance
$(X,Y)$-invariance
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 680-706
- Print publication:
- April 2024
-
- Article
- Export citation
A note on cyclic vectors in Dirichlet-type spaces in the unit ball of
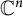 ${\mathbb C}^n$
${\mathbb C}^n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 January 2023, pp. 886-902
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weakly concave operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 18 January 2023, pp. 1-32
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation