Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T05:22:35.066Z Has data issue: false hasContentIssue false
  • English
  • Français

Dilations of Markovian semigroups of measurable Schur multipliers

Part of: Groups and semigroups of linear operators, their generalizations and applications Methods of category theory in functional analysis Selfadjoint operator algebras General theory of linear operators

Published online by Cambridge University Press:  05 April 2023

Cédric Arhancet
Cédric Arhancet*
Affiliation:
Lycée Lapérouse, 13 Rue Didier Daurat, 81000 Albi, France
*
e-mail: cedric.arhancet@protonmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Using probabilistic tools, we prove that any weak* continuous semigroup 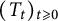$(T_t)_{t \geqslant 0}$ of self-adjoint unital completely positive measurable Schur multipliers acting on the space 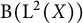$\mathrm {B}({\mathrm {L}}^2(X))$ of bounded operators on the Hilbert space 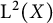${\mathrm {L}}^2(X)$, where X is a suitable measure space, can be dilated by a weak* continuous group of Markov $*$-automorphisms on a bigger von Neumann algebra. We also construct a Markov dilation of these semigroups. Our results imply the boundedness of the McIntosh’s 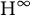${\mathrm {H}}^\infty $ functional calculus of the generators of these semigroups on the associated Schatten spaces and some interpolation results connected to 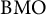${\mathrm {BMO}}$-spaces. We also give an answer to a question of Steen, Todorov, and Turowska on completely positive continuous Schur multipliers.

Keywords

SemigroupsdilationsSchatten spacespositive-definite kernelsfunctional calculusSchur multipliersBMO-spacescompletely positive maps

MSC classification

Primary: 47A20: Dilations, extensions, compressions 47D03: Groups and semigroups of linear operators 46L51: Noncommutative measure and integration 46M35: Abstract interpolation of topological vector spaces
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 3 , June 2024 , pp. 774 - 797
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author acknowledges support by the grant ANR-18-CE40-0021 (project HASCON) of the French National Research Agency ANR.

References

Arhancet, C., On Matsaev’s conjecture for contractions on noncommutative ${L}^p$ -spaces . J. Operator Theory 69(2013), no. 2, 387–421.10.7900/jot.2010dec29.1905CrossRefGoogle Scholar
Arhancet, C., Analytic semigroups on vector valued noncommutative ${L}^p$ -spaces . Stud. Math. 216(2013), no. 3, 271–290.CrossRefGoogle Scholar
Arhancet, C., Dilations of semigroups on von Neumann algebras and noncommutative ${L}^p$ -spaces . J. Funct. Anal. 276(2019), no. 7, 2279–2314.CrossRefGoogle Scholar
Arhancet, C., Dilations of Markovian semigroups of Fourier multipliers on locally compact groups . Proc. Amer. Math. Soc. 148(2020), no. 6, 2551–2563.10.1090/proc/14938CrossRefGoogle Scholar
Arhancet, C., Fackler, S., and Le Merdy, C., Isometric dilations and ${H}^{\infty }$ calculus for bounded analytic semigroups and Ritt operators . Trans. Amer. Math. Soc. 369(2017), 6899–6933.CrossRefGoogle Scholar
Arhancet, C. and Kriegler, C., Riesz transforms, Hodge–Dirac operators and functional calculus for multipliers, Lecture Notes in Mathematics, 2304, Springer, Cham, 2022.10.1007/978-3-030-99011-4CrossRefGoogle Scholar
Arhancet, C. and Kriegler, C.. Fourier–Stieltjes algebras, decomposable Fourier multipliers and amenability. Preprint, 2022. arXiv:2205.13823 Google Scholar
Arhancet, C. and Le Merdy, C., Dilation of Ritt operators on ${L}^p$ -spaces . Israel J. Math. 201(2014), no. 1, 373–414.CrossRefGoogle Scholar
Bekka, B., de la Pierre, P., and Valette, A., Kazhdan’s property (T), New Mathematical Monographs, 11, Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
Berg, C., Christensen, J., and Ressel, P., Harmonic analysis on semigroups. Theory of positive definite and related functions, Springer, New York, 1984.10.1007/978-1-4612-1128-0CrossRefGoogle Scholar
Blecher, D. and Le Merdy, C., Operator algebras and their modules—an operator space approach, London Mathematical Society Monographs. New Series, 30, Oxford Science Publications–Clarendon Press–Oxford University Press, Oxford, 2004.CrossRefGoogle Scholar
Bożejko, M., Positive and negative definite kernels on discrete groups. Lecture notes, Heidelberg University, 1987.Google Scholar
Cartier, P., Une étude des covariances mesurables (in French) [A study of measurable covariances]. In: Mathematical analysis and applications, part A, Adv. in Math. Suppl. Stud., 7a, Academic Press, New York–London, 1981, pp. 267–316.Google Scholar
Caspers, M., Harmonic analysis and BMO-spaces of free Araki-woods factors . Stud. Math. 246(2019), no. 1, 71–107.CrossRefGoogle Scholar
Caspers, M., Junge, M., Sukochev, F. and Zanin, D., BMO-estimates for non-commutative vector valued Lipschitz functions . J. Funct. Anal. 278(2020), no. 3, Article no. 108317, 39 pp.CrossRefGoogle Scholar
Duquet, C., Dilation properties of measurable Schur multipliers and Fourier multipliers. Preprint, 2022. arXiv:2202.06575 CrossRefGoogle Scholar
Engel, K.-J. and Nagel, R., One-parameter semigroups for linear evolution equations, Graduate Texts in Mathematics, 194, Springer, New York, 2000.Google Scholar
Fendler, G., Dilations of one parameter semigroups of positive contractions on ${L}^p$ spaces . Can. J. Math. 49(1997), no. 4, 736–748.CrossRefGoogle Scholar
Fendler, G., On dilations and transference for continuous one-parameter semigroups of positive contractions on ${\mathbf{\mathcal{L}}}^p$ -spaces . Ann. Univ. Sarav. Ser. Math. 9(1998), no. 1, 108317.Google Scholar
Ferguson, T., Mei, T., and Simanek, B., ${H}^{\infty }$ -calculus for semigroup generators on BMO . Adv. Math. 347(2019), 408–441.10.1016/j.aim.2019.02.027CrossRefGoogle Scholar
Haagerup, U. and Musat, M., Factorization and dilation problems for completely positive maps on von Neumann algebras . Commun. Math. Phys. 303(2011), no. 2, 555–594.CrossRefGoogle Scholar
Haase, M., The functional calculus for sectorial operators, Operator Theory: Advances and Applications, 169, Birkhäuser, Basel, 2006.CrossRefGoogle Scholar
Husain, T. and Warsi, S. A., Positive definite functions for the class ${L}_p(G)$ . Canadian J. Math. 27(1975), no. 5, 1149–1156.CrossRefGoogle Scholar
Hytönen, T., van Neerven, J., Veraar, M., and Weis, L., Analysis in Banach spaces: martingales and Littlewood–Paley theory. Vol. I, Springer, Cham, 2016.10.1007/978-3-319-48520-1CrossRefGoogle Scholar
Hytönen, T., van Neerven, J., Veraar, M., and Weis, L., Analysis in Banach spaces: probabilistic methods and operator theory. Vol. II, Springer, Cham, 2018.Google Scholar
Janson, S., Gaussian Hilbert spaces, Cambridge Tracts in Mathematics, 129, Cambridge University Press, Cambridge, 1997.CrossRefGoogle Scholar
Jiao, Y. and Wang, M., Noncommutative harmonic analysis on semigroups . Indiana Univ. Math. J. 66(2017), no. 2, 401–417.CrossRefGoogle Scholar
Junge, M. and Le Merdy, C., Dilations and rigid factorisations on noncommutative ${L}^p$ -spaces . J. Funct. Anal. 249(2007), 220–252.CrossRefGoogle Scholar
Junge, M., Le Merdy, C., and Xu, Q., ${H}^{\infty }$ functional calculus and square functions on noncommutative ${L}^p$ -spaces . Astérisque 305(2006), vi+138 pp.Google Scholar
Junge, M. and Mei, T., Noncommutative Riesz transforms—a probabilistic approach . Amer. J. Math. 132(2010), no. 3, 611–680.CrossRefGoogle Scholar
Junge, M. and Mei, T., BMO spaces associated with semigroups of operators . Math. Ann. 352(2012), no. 3, 691–743.10.1007/s00208-011-0657-0CrossRefGoogle Scholar
Junge, M. and Zeng, Q., Noncommutative martingale deviation and Poincaré type inequalities with applications . Probab. Theory Relat. Fields 161(2015), nos. 3–4, 449–507.CrossRefGoogle Scholar
König, H., Eigenvalue distribution of compact operators, Operator Theory: Advances and Applications, 16, Birkhäuser, Basel, 1986.CrossRefGoogle Scholar
Kunstmann, P. C. and Weis, L., Maximal   $L_p$ -regularity for parabolic equations, Fourier multiplier theorems and $H^{\infty}$ -functional calculus. In: Functional analytic methods for evolution equations, Lecture Notes in Mathematics, 1855, Springer, Berlin–Heidelberg, 2004, pp. 65–311.CrossRefGoogle Scholar
Le Merdy, C., Square functions, bounded analytic semigroups, and applications . In: Perspectives in operator theory, Banach Center Publications, 75, Polish Acad. Sci. Inst. Math., Warsaw, 2007, pp. 191–220.CrossRefGoogle Scholar
Li, B.-R., Introduction to operator algebras, World Scientific, Singapore, 1992.Google Scholar
Megginson, R. E., An introduction to Banach space theory, Graduate Texts in Mathematics, 183, Springer, New York, 1998.10.1007/978-1-4612-0603-3CrossRefGoogle Scholar
Mei, T., Tent spaces associated with semigroups of operators . J. Funct. Anal. 255(2008), no. 12, 3356–3406.CrossRefGoogle Scholar
Mercer, J., Linear transformations and functions of positive type . Proc. R. Soc. Lond. A 99(1921), no. 696, 19–38.Google Scholar
Nualart, D., The Malliavin calculus and related topics. 2nd ed., Springer, Berlin, 2006.Google Scholar
Palmer, T. W., Banach algebras and the general theory of *-algebras . Vol. 2, Encyclopedia of Mathematics and Its Applications, 79, Cambridge University Press, Cambridge, 2001.10.1017/CBO9780511574757CrossRefGoogle Scholar
Pisier, G., Non-commutative vector valued ${L}_p$ -spaces and completely $p$ -summing maps . Astérisque, 247(1998), vi+131 pp.Google Scholar
Ricard, É., A Markov dilation for self-adjoint Schur multipliers . Proc. Amer. Math. Soc. 136(2008), no. 12, 4365–4372.CrossRefGoogle Scholar
Sakai, S., C*-algebras and W*-algebras, Springer, New York, 1971.Google Scholar
Spronk, N., Measurable Schur multipliers and completely bounded multipliers of the Fourier algebras . Proc. Lond. Math. Soc. 89(2004), no. 1, 161–192.10.1112/S0024611504014650CrossRefGoogle Scholar
Steen, N. M., Todorov, I. G., and Turowska, L., Local operator multipliers and positivity . J. Funct. Anal. 267(2014), no. 1, 80–111.10.1016/j.jfa.2014.04.007CrossRefGoogle Scholar
Stratila, S., Modular theory in operator algebras, Editura Academiei Republicii Socialiste România, Bucharest; Abacus Press, Tunbridge Wells, 1981, translated from the Romanian by the author.Google Scholar
Todorov, I. G., Herz–Schur multipliers. Lectures at “Banach and Operator Algebras over Groups,” 2014.Google Scholar
Todorov, I. G., Interactions between harmonic analysis and operator theory . Serdica Math. J. 41(2015), no. 1, 13–34.Google Scholar
Todorov, I. G. and Turowska, L., Schur and operator multipliers . In: Banach algebras, Banach Center Publications, 91, Polish Acad. Sci. Inst. Math., Warsaw, 2009 (2010), pp. 385–410.Google Scholar
van Neerven, J., Stochastic evolution equations. ISEM lecture notes, 2007/08.Google Scholar
van Neerven, J., Veraar, M., and Weis, L., Stochastic integration in Banach spaces—a survey . In: Stochastic analysis: a series of lectures, Progress in Probability, 68, Birkhäuser, Basel, 2015, pp. 297–332.10.1007/978-3-0348-0909-2_11CrossRefGoogle Scholar