This paper is concerned with the numerical range and some related properties of the operator Δ/ S: T → AT – TB(T∈S), where A, B are (bounded linear) operators on the normed linear spaces X and Y. respectively, and S is a linear subspace of the space ℒ (Y, X) of all operators from Y to X. S is assumed to contain all finite operators, to be invariant under Δ, and to be suitably normed (not necessarily with the operator norm). Then the algebra numerical range of Δ/ S is equal to the difference of the algebra numerical ranges of A and B. When X = Y and S = ℒ (X), Δ is Hermitian (resp. normal) in ℒ (ℒ(X)) if and only if A–λ and B–λ are Hermitian (resp. normal) in ℒ(X)for some scalar λ;if X: = H is a Hilbert space and if S is a C *-algebra or a minimal norm ideal in ℒ(H)then any Hermitian (resp. normal) operator in S is of the form Δ/ S for some Hermitian (resp. normal) operators A and B. AT = TB implies A*T = TB* are hyponormal operators on the Hilbert spaces H1 and H2, respectively, and T is a Hilbert-Schmidt operator from H2 to H1.

We show that a bounded linear operator on a uniformly convex space may be perturbed by a compact operator of arbitrarily small norm to yield an operator which attains its numerical radius.

A double triangle subspace lattice in a Hilbert space H is a 5-element set of subspaces of H, containing (0) and H, with each pair of non-trivial elements intersecting in (0) and spanning H. It is shown that if any pair of non-trivial elements has a closed vector sum the double triangle is both non-reflexive and non-transitive. A double triangle in H⊕H is an operator double triangle if each non-trivial elements is the graph of an operator acting on H. A sufficient condition is given for any operator double triangle to be non-reflexive.

Stampfli and Embry have shown that a point of the numerical range of an operator is extreme if and only if a set of vectors corresponding to it is linear. This is generalized here to show that a point of the closure of the numerical range is extreme if and only if a corresponding set of sequences forms a linear space. A more geometric alternative proof is given for a theorem of Das and Garske concerning weak convergence to zero at the unattained extreme points of the closure of the numerical range.The result is shown to hold also for lone extreme points of the numerical range which lie on line segments on its boundary. Further, a bound is obtained on the norm of the weak limit of the weakly convergent sequences corresponding to points on a line segment on the boundary of numerical range.

Let D ⊂ Rn be a bounded domain and L: dom L ⊂ L2 (D) → L2 (D) be a self-adjoint operator of finite dimensional kernel. Let f: D × R → R be a function satisfying the Carathéodory condition. Assume that there are constants λ > 0 and δ ∈ [0, 1] such that and that .

Then with the aid of a generalized Krasnosel'skii's theorem it has been proved that under conditions exactly analogous to those of Landesman and Lazer there exists u ∈ L2(D) such that L(u)(x) = f(x, u(x)) for ∀x ∈ D. This result is then used to prove the existence of weak solutions of nonlinesr elliptic boundary value problems.

Other abstract results applicable to ordinary and partial differential equations have also been proved.

A joint spectral theorem for an n-tuple of doubly commuting unbounded normal operators in a Hilbert space is proved by using the techniques of GB*-algebras.

The class ϕ+(X, Y) of semi-Fredholm transformations consists of those transformations T: X → Y for which α(T) = dim ker T < ∞ and for which T(X) is closed. It forms an open subset of B (X, Y) closed under perturbation by compact transformations and is a particularly important class of transformation since T is Fredholm if and only if T ∈ ϕ+ (X, Y) and T′ ∈ ϕ+ (Y′. X′). The realization that elements of ϕ+ (X, Y) have very simple nonstandard characterizations lead the author to consider the possibility of finding an analogous open class of transformation which is closed under perturbation by weakly compact transformations. Consequently this paper investigates two related classes which contain ϕ+ (X, Y). The first such class coincides with the class of Tauberian transformations whilst the second consists of those transformations which have Tauberian extensions on the nonstandard hulls. The Tauberian transformations are closed under perturbation by weakly compact transformations but in general are not open. The “super” Tauberian transformations are closed under perturbation by super weakly compact transformations and in fact form an open subset of B(X, Y).

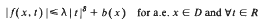
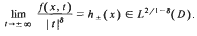
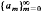Let B(H) be the Banach algebra of all (bounded linear) operators on an infinite-dimensional separable complex Hilbert space H and let be a bounded sequence of positive real numbers. For a given injective operator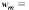 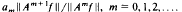A in B(H) and a non-zero vector f in H, we put We define a weighted shift 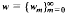Tw with the weight sequence on the Hilbert space 1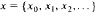2 of all square-summable complex sequences by 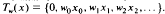. 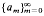The main object of this paper is to characterize the invariant subspace lattice of Tw under various nice conditions on the operator A and the sequence .

A subspace of a Banach space is called an operator range if it is the continuous linear image of a Banach space. Operator ranges and operator ideals with fixed range space are investigated. Properties of strictly singular, strictly cosingular, weakly sequentially precompact, and other classes of operators are derived. Perturbation theory and closed semi-Fredholm operators are discussed in the final section.

The main result of this paper shows that the existence of commuting normal extension (c.n.e.) for an arbitrary family of commuting subnormal operators can be determined by considering appropriate families of multivariable weighted shifts. In proving this some known criteria for c.n.e. are generalized. It is also shown that a family of jointly quasi-normal operators has c.n.e.

An elementary and self-contained account of analytic Jordan decomposition of matrix-valued analytic functions is given. An integral representation for their eigenvalues is obtained. This leads to estimates of the differences in eigenvalues and the number of points of degeneracy.

Let ˜ be an equivalence relation on a topological space X. A point x ε X i s stable with respect to ˜ if it is in the interior of an equivalence class. We may also add, if ambiguity arises, that x is stable under perturbations in X. Let E be a Banach space, and let L(E) be the Banach space of continuous linear endomorphisms of E, with norm given by |T| = sup{ |T(x) | : |x| = 1}. In this paper we discuss stability of elements of L(E) with respect to some natural equivalence relations.