We give a simplified proof of the complex inversion formula for semigroups and, more generally, solution families for scalar-type Volterra equations, including the stronger versions on unconditional martingale differences (UMD) spaces. Our approach is based on (elementary) Fourier analysis.

In this article we consider Re-nnd solutions of the equation AXB=C with respect to X, where A,B,C are given matrices. We give necessary and sufficient conditions for the existence of Re-nnd solutions and present a general form of such solutions. As a special case when A=I we obtain the results from a paper of Groß (‘Explicit solutions to the matrix inverse problem AX=B’, Linear Algebra Appl.289 (1999), 131–134).

Several rather general sufficient conditions for the extrapolation of the calculus of generalized Dirac operators from L2 to Lp are established. As consequences, we obtain some embedding theorems, quadratic estimates and Littlewood–Paley theorems in terms of this calculus in Lebesgue spaces. Some further generalizations, utilised in Part II devoted to applications, which include the Kato square root model, are discussed. We use resolvent approach and show the irrelevance of the semigroup one. Auxiliary results include a high order counterpart of the Hilbert identity, the derivation of new forms of ‘off-diagonal’ estimates, and the study of the structure of the model in Lebesgue spaces and its interpolation properties. In particular, some coercivity conditions for forms in Banach spaces are used as a substitution of the ellipticity ones. Attention is devoted to the relations between the properties of perturbed and unperturbed generalized Dirac operators. We do not use any stability results.

We derive necessary and sufficient conditions for the existence of a time-periodic solution to the abstract Cauchy problem.

The paper introduces and studies the weighted g-Drazin inverse for bounded linear operators between Banach spaces, extending the concept of the weighted Drazin inverse of Rakočević and Wei (Linear Algebra Appl. 350 (2002), 25–39) and of Cline and Greville (Linear Algebra Appl. 29 (1980), 53–62). We use the Mbekhta decomposition to study the structure of an operator possessing the weighted g-Drazin inverse, give an operator matrix representation for the inverse, and study its continuity. An open problem of Rakočević and Wei is solved.

We show that generalized Gaussian estimates for selfadjoint semigroups (e-tA)t ∈ R+ on L2 imply Lp boundedness of Riesz means and other regularizations of the Schrödinger group (eitA)t ∈ R. This generalizes results restricted to semigroups with a heat kernel, which are due to Sjöstrand, Alexopoulos and more recently Carron, Coulhon and Ouhabaz. This generalization is crucial for elliptic operators A that are of higher order or have singular lower order terms since, in general, their semigroups fail to have a heat kernel.

We derive the spectrum of the Laplace–Beltrami operator on the quotient orbifold of the nonhyperbolic triangle groups.

Blackwell (1951), in his seminal work on comparison of experiments, ordered two experiments using a dilation ordering: one experiment, Y, is ‘more spread out’ in the sense of dilation than another one, X, if E(c(Y))≥E(c(X)) for all convex functions c. He showed that this ordering is equivalent to two other orderings, namely (i) a total time on test ordering and (ii) a martingale relationship E(Yʹ | Xʹ)=Xʹ, where (Xʹ,Yʹ) has a joint distribution with the same marginals as X and Y. These comparisons are generalized to balayage orderings that are defined in terms of generalized convex functions. These balayage orderings are equivalent to (i) iterated total integral of survival orderings and (ii) martingale-type orderings which we refer to as k-mart orderings. These comparisons can arise naturally in model fitting and data confidentiality contexts.

The paper introduces and studies the weighted g-Drazin inverse for bounded linear operators between Banach spaces, extending the concept of the weighted Drazin inverse of Rakočević and Wei (Linear Algebra Appl. 350 (2002), 25–39) and of Cline and Greville (Linear Algebra Appl. 29(1980), 53–62). We use the Mbekhta decomposition to study the structure of an operator possessing the weighted g-Drazin inverse, give an operator matrix representation for the inverse, and study its continuity. An open problem of Rakočević and Wei is solved.

Let (X, ρ, μ)d, θ be a space of homogeneous type with d < 0 and θ ∈ (0, 1], b be a para-accretive function, ε ∈ (0, θ], ∣s∣ > ∈ and a0 ∈ (0, 1) be some constant depending on d, ∈ and s. The authors introduce the Besov space bBspq (X) with a0 > p ≧ ∞, and the Triebel-Lizorkin space bFspq (X) with a0 > p > ∞ and a0 > q ≧∞ by first establishing a Plancherel-Pôlya-type inequality. Moreover, the authors establish the frame and the Littlewood-Paley function characterizations of these spaces. Furthermore, the authors introduce the new Besov space b−1 Bs (X) and the Triebel-Lizorkin space b−1 Fspq (X). The relations among these spaces and the known Hardy-type spaces are presented. As applications, the authors also establish some real interpolation theorems, embedding theorems, T b theorems, and the lifting property by introducing some new Riesz operators of these spaces.

Let G be a compact abelian group and 1< p < ∞. It is known that the spectrum σ (Tψ) of a Fourier p–multiplier operator Tψ acting in Lp(G), may fail to coincide with its natural spectrum ψ(Г) if p ≠ 2; here Γ is the dual group to G and the bar denotes closure in C. Criteria are presented, based on geometric, topological and/or algebraic properties of the compact set σ(Tψ), which are sufficient to ensure that the equality σ(Tψ) = ψ(Г)holds.

We develop several iterative methods for computing generalized inverses using both first and second order optimization methods in C*-algebras. Known steepest descent iterative methods are generalized in C*-algebras. We introduce second order methods based on the minimization of the norms ‖Ax − b‖2 and ‖x‖2 by means of the known second order unconstrained minimization methods. We give several examples which illustrate our theory.

Inspired by a statement of W. Luh asserting the existence of entire functions having together with all their derivatives and antiderivatives some kind of additive universality or multiplicative universality on certain compact subsets of the complex plane or of, respectively, the punctured complex plane, we introduce in this paper the new concept of U-operators, which are defined on the space of entire functions. Concrete examples, including differential and antidifferential operators, composition, multiplication and shift operators, are studied. A result due to Luh, Martirosian and Müller about the existence of universal entire functions with gap power series is also strengthened.

The eigentime identity is proved for continuous-time reversible Markov chains with Markov generator L. When the essential spectrum is empty, let {0 = λ0 < λ1 ≤ λ2 ≤ ···} be the whole spectrum of L in L2. Then ∑n≥1 λn -1 < ∞ implies the existence of the spectral gap α of L in L∞. Explicit formulae are presented in the case of birth–death processes and from these formulae it is proved that ∑n≥1 λn -1 < ∞ if and only if α > 0.

In this paper we continue to modify and expand a technique due to Enflo for producing nontrivial hyperinvariant subspaces for quasinilpotent operators, and thereby obtain such subspaces for some additional quasinilpotent operators on Hilbert space. We also obtain a structure theorem for a certain class of operators.

We show that the operator-valued Marcinkiewicz and Mikhlin Fourier multiplier theorem are valid if and only if the underlying Banach space is isomorphic to a Hilbert space.

We develop a theory of ergodicity for unbounded functions ø: J → X, where J is a subsemigroup of a locally compact abelian group G and X is a Banach space. It is assumed that ø is continuous and dominated by a weight w defined on G. In particular, we establish total ergodicity for the orbits of an (unbounded) strongly continuous representation T: G → L(X) whose dual representation has no unitary point spectrum. Under additional conditions stability of the orbits follows. To study spectra of functions, we use Beurling algebras L1w(G) and obtain new characterizations of their maximal primary ideals, when w is non-quasianalytic, and of their minimal primary ideals, when w has polynomial growth. 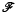It follows that, relative to certain translation invariant function classes , the reduced Beurling spectrum of ø is empty if and only if ø ∈ . For the zero class, this is Wiener's tauberian theorem.

We consider random dynamical systems with randomly chosen jumps on infinite-dimensional spaces. The choice of deterministic dynamical systems and jumps depends on a position. The system generalizes dynamical systems corresponding to learning systems, Poisson driven stochastic differential equations, iterated function system with infinite family of transformations and random evolutions. We will show that distributions which describe the dynamics of this system converge to an invariant distribution. We use recent results concerning asymptotic stability of Markov operators on infinite-dimensional spaces obtained by T. Szarek.

The purpose of this paper is to provide a detailed treatment of the behaviour of essential spectra of closed densely defined linear operators subjected to additive perturbations not necessarily belonging to any ideal of the algebra of bounded linear operators. If A denotes a closed densely defined linear operator on a Banach space X, our approach consists principally in considering the class of A-closable operators which, regarded as operators in ℒ(XA, X) (where XA denotes the domain of A equipped with the graph norm), are contained in the set of A-Fredholm perturbations (see Definition 1.2). Our results are used to describe the essential spectra of singular neutron transport equations in bounded geometries.

In this paper, we study Markov fluid queues where the net fluid rate to a single-buffer system varies with respect to the state of an underlying continuous-time Markov chain. We present a novel algorithmic approach to solve numerically for the steady-state solution of such queues. Using this approach, both infinite- and finite-buffer cases are studied. We show that the solution of the infinite-buffer case is reduced to the solution of a generalized spectral divide-and-conquer (SDC) problem applied on a certain matrix pencil. Moreover, this SDC problem does not require the individual computation of any eigenvalues and eigenvectors. Via the solution for the SDC problem, a matrix-exponential representation for the steady-state queue-length distribution is obtained. The finite-buffer case, on the other hand, requires a similar but different decomposition, the so-called additive decomposition (AD). Using the AD, we obtain a modified matrix-exponential representation for the steady-state queue-length distribution. The proposed approach for the finite-buffer case is shown not to have the numerical stability problems reported in the literature.