Refine listing
Actions for selected content:
292 results in 47Axx
Invariant subspaces in the bidisc and commutators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-242
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Generation of generators of holomorphic semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-269
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
The spectral theorem for well-bounded operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 3 / June 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-351
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
On strongly stable approximations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-260
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
The spectra of weighted mean operators on bν0
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 242-250
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
Hyponormal operators on uniformly smooth spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 150-159
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
Operator approximations with stable elgenvalues
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 250-257
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Eigenelements of perturbed operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-148
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
On the spectrum of C1 as an operator on bv0
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-86
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
H∞ functional calculus of elliptic operators with C∞ coefficients on Lp spaces of smooth domains
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 113-123
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
The non-emptiness of joint spectral subsets of euclidean n-space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 300-306
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
On the Pták homomorphism theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-333
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
Fractional powers of generators of equicontinuous semigroups and fractional derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 473-504
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
On the error estimates for the Rayleigh-Schrödinger series and the Kato-Rellich perturbation series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 456-468
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
Support of the joint spectral measure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 74-80
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
On a representation of continuous Volterra right inverses to the derivative in the spaces of infinitely differentiable functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-142
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
Relatively central operators on Archimedean vector lattices II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-298
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
Subsets characterizing the closure of the numerical range
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-4
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
Subspaces associated with boundary points of the numerical range
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-27
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Generlized Fredholm transformations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 89-97
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
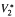 , For example, M is studied when the commutator is self-adjoint or of finite rank.
, For example, M is studied when the commutator is self-adjoint or of finite rank.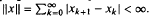 .
.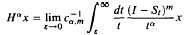
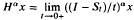
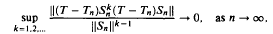
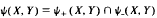 en forms an open subset of
en forms an open subset of 