Refine listing
Actions for selected content:
292 results in 47Axx
The generalized condition numbers of bounded linear operators in Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-290
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Generalized Weyl's theorem and hyponormal operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 291-302
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Homogeneous quasi-invariant subspaces of the fock space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 399-408
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
An extension of Henrici theorem for the joint approximate spectrum of commuting spectral operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-246
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Lacunas in the Support of the Weyl Calculus for Two Hermitian Matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-124
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Two Results About H∞ Functional Calculus on Analytic umd Banach Spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-378
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Additive results for the generalized Drazin inverse
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 115-126
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
The perturbation theory for the Drazin inverse and its applications II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-198
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Essentially commutative C*-algebras with essential spectrum homeomorphic to S2n−1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-210
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Compactness properties for perturbed semigroups and application to transport equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-40
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Spectral and asymptotic properties of resolvent-dominated operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 181-201
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
The fundamental matrix of singularly perturbed Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 679-697
- Print publication:
- September 1999
-
- Article
- Export citation
Boundedness of rough singular integral operators on homogeneous Herz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-223
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation
Subordination in the sense of Bochner and a related functional calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 368-396
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Ergodicity and differences of functions on semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-265
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Modified cauchy kernels and functional calculus for operators on Banach space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-99
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Spectral and asymptotic properties of dominated operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-31
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Banach space operators with a bounded H∞ functional calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-89
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Some trace inequalities for operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-286
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
Approximations of positive operators and continuity of the spectral radius III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 330-340
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
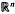 ) functions and Ricci-Stein oscillatory singular integral operators. Some new results are obtained.
) functions and Ricci-Stein oscillatory singular integral operators. Some new results are obtained.