Refine listing
Actions for selected content:
292 results in 47Axx
REPRESENTATION THEOREMS FOR INDEFINITE QUADRATIC FORMS REVISITED
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 169-189
- Print publication:
- January 2013
-
- Article
- Export citation
Cyclicity of singular inner functions from the corona theorem
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 31 May 2012, pp. 815-824
- Print publication:
- October 2012
-
- Article
- Export citation
SPECTRAL STABILITY ESTIMATES FOR ELLIPTIC OPERATORS SUBJECT TO DOMAIN TRANSFORMATIONS WITH NON-UNIFORMLY BOUNDED GRADIENTS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 24 February 2012, pp. 324-348
- Print publication:
- July 2012
-
- Article
- Export citation
SMALL ESSENTIAL SPECTRAL RADIUS PERTURBATIONS OF OPERATORS WITH TOPOLOGICAL UNIFORM DESCENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 30 August 2011, pp. 26-45
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
Hypercyclic and mixing operator semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 27 June 2011, pp. 761-782
-
- Article
-
- You have access
- Export citation
ALGEBRAIC ASPECTS OF SPECTRAL THEORY
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 63-88
- Print publication:
- January 2011
-
- Article
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ENDPOINT ESTIMATES FOR COMMUTATORS OF RIESZ TRANSFORMS ASSOCIATED WITH SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 367-389
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
SPECTRAL RADIUS ALGEBRAS AND C0 CONTRACTIONS. II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 September 2010, pp. 91-104
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
ITERATED LAVRENTIEV REGULARIZATION FOR NONLINEAR ILL-POSED PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 19 April 2010, pp. 191-217
-
- Article
-
- You have access
- Export citation
TENSOR EXTENSION PROPERTIES OF C(K)-REPRESENTATIONS AND APPLICATIONS TO UNCONDITIONALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 March 2010, pp. 205-230
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Some Applications of the Perturbation Determinant in Finite von Neumann Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 133-156
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Projectors on the Generalized Eigenspaces for Neutral Functional Differential Equations in Lp Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-93
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Rate of growth of frequently hypercyclic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 39-59
-
- Article
-
- You have access
- Export citation
INVERSE SPECTRAL PROBLEMS FOR SINGULAR RANK-ONE PERTURBATIONS OF A HILL OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 421-428
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
A KATO PERTURBATION-TYPE RESULT FOR OPEN LINEAR RELATIONS IN NORMED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 10 March 2009, pp. 85-101
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
LIMITS OF HYPERCYCLIC AND SUPERCYCLIC OPERATOR MATRICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 367-376
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
WEIGHTED ESTIMATES FOR SINGULAR INTEGRAL OPERATORS WITH NONSMOOTH KERNELS AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 377-417
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
INVARIANT SUBSPACES IN THE BIDISC AND WANDERING SUBSPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 367-374
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
REMARKS ON ℓ1 AND
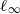 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 345-365
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
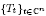 with holomorphic dependence on the parameter
with holomorphic dependence on the parameter 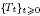 .
.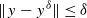 resulting in the convergence of the method as
resulting in the convergence of the method as 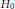
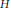
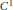
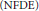
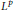
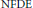
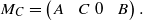
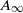 weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted
weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted 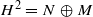 . Using the wandering subspace of
. Using the wandering subspace of 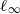 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
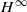 -calculus, and give a complete characterization of this condition in the case of Banach spaces which are
-calculus, and give a complete characterization of this condition in the case of Banach spaces which are 