Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T15:25:49.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Applications of the Perturbation Determinant in Finite von Neumann Algebras

Part of: Individual linear operators as elements of algebraic systems General theory of linear operators

Published online by Cambridge University Press:  20 November 2018

Konstantin A. Makarov  and
Anna Skripka
Konstantin A. Makarov
Affiliation:
Konstantin A. Makarov, Department of Mathematics, University of Missouri, Columbia, MO 65211, USA, e-mail: makarovk@missouri.edu
Anna Skripka
Affiliation:
Anna Skripka, Department of Mathematics, Texas A&M University, College Station, TX 77843, USA, e-mail: askripka@math.tamu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the finite von Neumann algebra setting, we introduce the concept of a perturbation determinant associated with a pair of self-adjoint elements 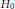${{H}_{0}}$ and 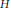$H$ in the algebra and relate it to the concept of the de la Harpe–Skandalis homotopy invariant determinant associated with piecewise 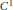${{C}^{1}}$-paths of operators joining 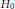${{H}_{0}}$ and 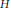$H$. We obtain an analog of Krein's formula that relates the perturbation determinant and the spectral shift function and, based on this relation, we derive subsequently (i) the Birman–Solomyak formula for a general non-linear perturbation, (ii) a universality of a spectral averaging, and (iii) a generalization of the Dixmier–Fuglede–Kadison differentiation formula.

Keywords

perturbation determinanttrace formulaevon Neumann algebras

MSC classification

Secondary: 47A55: Perturbation theory 47A53: (Semi-) Fredholm operators; index theories 47C15: Operators in $C^*$- or von Neumann algebras
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 1 , 01 February 2010 , pp. 133 - 156
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] A. B., Aleksandrov, The multiplicity of the boundary values of inner functions. Sov. J. Contemporary Math. Anal. 22(1987), no. 5, 74-87.Google Scholar
[2] N. A., Azamov, A. L., Carey, P. G., Dodds, and F. A., Sukochev, Operator integrals, spectral shift, and spectral flow. Canad. J. Math. 61(2009), no. 2, 241-263. doi:10.4153/CJM-2009-012-0Google Scholar
[3] N. A., Azamov, A. L., Carey, and F. A., Sukochev, The spectral shift function and spectral flow. Comm. Math. Phys. 276(2007), no. 1, 51-91. doi:10.1007/s00220-007-0329-9Google Scholar
[4] N. A., Azamov, P. G., Dodds, and F. A., Sukochev, The Krein spectral shift function in semifinite von Neumann algebras. Integral Equations Operator Theory 55(2006), no. 3, 347-362. doi:10.1007/s00020-006-1441-5Google Scholar
[5] Benameur, M.-T., A. L., Carey, J., Phillips, A., Rennie, F. A., Sukochev, and K. P., Wojciechowski, An analytic approach to spectral flow in von Neumann algebras. In: Analysis, Geometry and Topology of Elliptic Operators. World Sci. Publ., Hackensack, NJ, 2006, pp. 297-352.Google Scholar
[6] Birman, M. Š. and A. B., Pushnitski, Spectral shift function, amazing and multifaceted. Integral Equations Operator Theory 30(1998), no. 2, 191-199. doi:10.1007/BF01238218Google Scholar
[7] Birman, M. Š. and M. Z., Solomyak, Remarks on the spectral shift function. Zap. Naučn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 27(1972), 33-46 (Russian); English transl. in J. Soviet Math. 3(1975), no. 4, 408-419.Google Scholar
[8] L. G., Brown, Lidskiĭ's theorem in the type II case. In: Geometric Methods in Operator Algebras. Pitman Res. Notes Math. Ser. 123. Longman Sci. Tech., Harlow, 1986, pp. 1-35.Google Scholar
[9] R. W., Carey and J. D., Pincus, Mosaics, principal functions, and mean motion in von Neumann algebras. Acta Math. 138(1977), no. 3-4, 153-218. doi:10.1007/BF02392315Google Scholar
[10] Daleckkiĭ, Yu. L., S. G., Krein, Integration and differentiation of functions of Hermitian operators and applications to the theory of perturbations. (Russian) Voronež. Gos. Univ. Trudy Sem. Funkcional. Anal. 1956(1956), no. 1, 81-105.Google Scholar
[11] J., Dixmier, von Neumann Algebras. North-Holland, Amsterdam, 1981.Google Scholar
[12] B., Fuglede and R. V., Kadison, Determinant theory in finite factors. Ann. Math. 55(1952), 520-530. doi:10.2307/1969645Google Scholar
[13] F., Gesztesy and K. A.Makarov, SL2(R), exponential representation of Herglotz functions, and spectral averaging. Algebra i Analiz 15(2003), no. 3, 104-144 (Russian); English transl. in St. Petersburg Math. J. 15(2004), no. 3, 393-418.Google Scholar
[14] F., Gesztesy, K. A., Makarov, and S. N., Naboko, The spectral shift operator. In: Mathematical Results in Quantum Mechanics. Oper. Theory Adv. Appl. 108, Birkhäuser, Basel, 1999, pp. 59-90.Google Scholar
[15] F., Gesztesy and E., Tsekanovskii, On matrix-valued Herglotz functions. Math. Nachr. 218(2000), 61-138. doi:10.1002/1522-2616(20010)218:1h61::AID-MANA61i3.0.CO;2-DGoogle Scholar
[16] U., Haagerup, and H., Schultz, Brown measures of unbounded operators affiliated with a finite von Neumann algebra. Math. Scand. 100(2007), no. 2, 209-263.Google Scholar
[17] P., de la Harpe, and G., Skandalis, Déterminant associé `a une trace sur une algèbre de Banach. Ann. Inst. Fourier (Grenoble) 34(1984), no. 1, 241-260.Google Scholar
[18] V. A., Javrjan, On the regularized trace of the difference between two singular Sturm-Liouville operators, Sov. Math. Dokl. 7(1966), 888-891.Google Scholar
[19] V. A., Javrjan, A certain inverse problem for Sturm-Liouville operators. Izv. Akad. Nauk Armjan. SSR Ser. Math. 6(1971), no. 2-3, 246-251 (Russian).Google Scholar
[20] V., Kostrykin, K. A., Makarov, and A., Skripka, The Birman-Schwinger principle in von Neumann algebras of finite type. J. Funct. Anal. 247(2007), no. 2, 492-508. doi:10.1016/j.jfa.2006.12.001Google Scholar
[21] M. G., Krein, On the trace formula in perturbation theory. Matem. Sbornik 33(1953), 597-626 (Russian).Google Scholar
[22] M. G., Krein, Some new studies in the theory of perturbations of self-adjoint operators. In: 1964 First Math. Summer School, Part I. Izdat. “Naukova Dumka”, Kiev pp. 103-187 (Russian).Google Scholar
[23] I. M., Lifshits, On a problem of the theory of perturbations connected with quantum statistics. Uspehi Matem. Nauk 7(1952), 171-180 (Russian).Google Scholar
[24] Łojasiewicz, S., An Introduction to the Theory of Real Functions. Third edition. Wiley Interscience, Chichester, 1988.Google Scholar
[25] J., Phillips, Self-adjoint Fredholm operators and spectral flow. Canad. Math. Bull. 39(1996), no. 4, 460-467.Google Scholar
[26] J., Phillips, Spectral flow in type I and II factors-a new approach. In: Cyclic Cohomology and Noncommutative Geometry. Fields Inst. Commun. 17. American Mathematical Society, Providence, RI, 1997, pp. 137-153..Google Scholar
[27] M., Reed and B., Simon, Methods of modern mathematical physics. I. Functional analysis. Academic Press, New York, 1972.Google Scholar
[28] B., Simon, Spectral averaging and the Krein spectral shift. Proc. Amer. Math. Soc. 126(1998), no. 5, 1409-1413. doi:10.1090/S0002-9939-98-04261-0Google Scholar
[29] A., Skripka, On properties of the _-function in semi-finite von Neumann algebras. Integral Equations Operator Theory 62(2008), no. 2, 247-267. doi:10.1007/s00020-008-1617-2Google Scholar
[30] D. J., Thouless, Electrons in disordered systems and the theory of localization. Phys. Rep. 13(1974), no. 3, 93-142.Google Scholar
[31] D. R., Yafaev, Mathematical Scattering Theory. Translations of Mathematical Monographs 105. American Mathematical Society, Providence, RI, 1992.Google Scholar