We present some properties of orthogonality and relate them with support disjoint and norm inequalities in $p$-Schatten ideals. In addition, we investigate the problem of characterization of norm-parallelism for bounded linear operators. We consider the characterization of the norm-parallelism problem in $p$-Schatten ideals and locally uniformly convex spaces. Later on, we study the case when an operator is norm-parallel to the identity operator. Finally, we give some equivalence assertions about the norm-parallelism of compact operators. Some applications and generalizations are discussed for certain operators.

Let $G$ be an infinite graph on countably many vertices and let $\unicode[STIX]{x1D6EC}$ be a closed, infinite set of real numbers. We establishthe existence of an unbounded self-adjoint operator whose graph is $G$ and whose spectrum is $\unicode[STIX]{x1D6EC}$ .

In this paper we define B-Fredholm elements in a Banach algebra A modulo an ideal J of A. When a trace function is given on the ideal J, it generates an index for B-Fredholm elements. In the case of a B-Fredholm operator T acting on a Banach space, we prove that its usual index ind(T) is equal to the trace of the commutator [T, T0], where T0 is a Drazin inverse of T modulo the ideal of finite rank operators, extending Fedosov's trace formula for Fredholm operators (see Böttcher and Silbermann [Analysis of Toeplitz operators, 2nd edn (Springer, 2006)]. In the case of a primitive Banach algebra, we prove a punctured neighbourhood theorem for the index.

We obtain intertwining dilation theorems for non-commutative regular domains 𝒟f and non-commutative varieties 𝒱J in B(𝓗)n, which generalize Sarason and Szőkefalvi-Nagy and Foiaş's commutant lifting theorem for commuting contractions. We present several applications including a new proof for the commutant lifting theorem for pure elements in the domain 𝒟f (respectively, variety 𝒱J ) as well as a Schur-type representation for the unit ball of the Hardy algebra associated with the variety 𝒱J. We provide Andô-type dilations and inequalities for bi-domains 𝒟f ×c 𝒟g consisting of all pairs (X,Y ) of tuples X := (X1,…, Xn1) ∊ 𝒟f and Y := (Y1,…, Yn2) ∊ 𝒟g that commute, i.e. each entry of X commutes with each entry of Y . The results are new, even when n1 = n2 = 1. In this particular case, we obtain extensions of Andô's results and Agler and McCarthy's inequality for commuting contractions to larger classes of commuting operators. All the results are extended to bi-varieties 𝒱J1×c 𝒱J2, where 𝒱J1 and 𝒱J2 are non-commutative varieties generated by weak-operator-topology-closed two-sided ideals in non-commutative Hardy algebras. The commutative case and the matrix case when n1 = n2 = 1 are also discussed.

It is not known whether the inverse of a frequently hypercyclic bilateral weighted shift on c0(ℤ) is again frequently hypercyclic. We show that the corresponding problem for upper frequent hypercyclicity has a positive answer. We characterise, more generally, when bilateral weighted shifts on Banach sequence spaces are (upper) frequently hypercyclic.

Let ${\mathcal{H}}=\mathbb{C}^{n}\otimes {\mathcal{E}}$ be the tensor product of a Euclidean space $\mathbb{C}^{n}$ and a separable Hilbert space ${\mathcal{E}}$. Our main object is the operator $G=I_{n}\otimes S+A\otimes I_{{\mathcal{E}}}$, where $S$ is a normal operator in ${\mathcal{E}}$, $A$ is an $n\times n$ matrix, and $I_{n},I_{{\mathcal{E}}}$ are the unit operators in $\mathbb{C}^{n}$ and ${\mathcal{E}}$, respectively. Numerous differential operators with constant matrix coefficients are examples of operator $G$. In the present paper we show that $G$ is similar to an operator $M=I_{n}\otimes S+\hat{D}\times I_{{\mathcal{E}}}$ where $\hat{D}$ is a block matrix, each block of which has a unique eigenvalue. We also obtain a bound for the condition number. That bound enables us to establish norm estimates for functions of $G$, nonregular on the closed convex hull $\operatorname{co}(G)$ of the spectrum of $G$. The functions $G^{-\unicode[STIX]{x1D6FC}}\;(\unicode[STIX]{x1D6FC}>0)$ and $(\ln G)^{-1}$ are examples of such functions. In addition, in the appropriate situations we improve the previously published estimates for the resolvent and functions of $G$ regular on $\operatorname{co}(G)$. Since differential operators with variable coefficients often can be considered as perturbations of operators with constant coefficients, the results mentioned above give us estimates for functions and bounds for the spectra of differential operators with variable coefficients.

We study the convex feasibility problem in $\text{CAT}(\unicode[STIX]{x1D705})$ spaces using Mann’s iterative projection method. To do this, we extend Mann’s projection method in normed spaces to $\text{CAT}(\unicode[STIX]{x1D705})$ spaces with $\unicode[STIX]{x1D705}\geq 0$ , and then we prove the $\unicode[STIX]{x1D6E5}$ -convergence of the method. Furthermore, under certain regularity or compactness conditions on the convex closed sets, we prove the strong convergence of Mann’s alternating projection sequence in $\text{CAT}(\unicode[STIX]{x1D705})$ spaces with $\unicode[STIX]{x1D705}\geq 0$ .

We consider equivariant continuous families of discrete one-dimensional operators over arbitrary dynamical systems. We introduce the concept of a pseudo-ergodic element of a dynamical system. We then show that all operators associated to pseudo-ergodic elements have the same spectrum and that this spectrum agrees with their essential spectrum. As a consequence we obtain that the spectrum is constant and agrees with the essential spectrum for all elements in the dynamical system if minimality holds.

New inequalities relating the norm $n(X)$ and the numerical radius $w(X)$ of invertible bounded linear Hilbert space operators were announced by Hosseini and Omidvar [‘Some inequalities for the numerical radius for Hilbert space operators’, Bull. Aust. Math. Soc.94 (2016), 489–496]. For example, they asserted that $w(AB)\leq$ $2w(A)w(B)$ for invertible bounded linear Hilbert space operators $A$ and $B$ . We identify implicit hypotheses used in their discovery. The inequalities and their proofs can be made good by adding the extra hypotheses which take the form $n(X^{-1})=n(X)^{-1}$ . We give counterexamples in the absence of such additional hypotheses. Finally, we show that these hypotheses yield even stronger conclusions, for example, $w(AB)=w(A)w(B)$ .

Let X be a complex Banach space and denote by ${\cal L}(X)$ the Banach algebra of all bounded linear operators on X. We prove that if φ: ${\cal L}(X) \to {\cal L}(X)$ is a linear surjective map such that for each $T \in {\cal L}(X)$ and x ∈ X the local spectrum of φ(T) at x and the local spectrum of T at x are either both empty or have at least one common value, then φ(T) = T for all $T \in {\cal L}(X)$ . If we suppose that φ always preserves the modulus of at least one element from the local spectrum, then there exists a unimodular complex constant c such that φ(T) = cT for all $T \in {\cal L}(X)$ .

The theory of almost invariant half-spaces for operators on Banach spaces was begun recently and is now under active development. Much less attention has been given to almost invariant half-spaces for operators on Hilbert space, where some techniques and results are available that are not present in the more general context of Banach spaces. In this note, we begin such a study. Our much simpler and shorter proofs of the main theorems have important consequences for the matricial structure of arbitrary operators on Hilbert space.

This paper deals with the spectral properties of self-adjoint Schrödinger operators with δʹ-type conditions on infinite regular trees. Firstly, we discuss the semi-boundedness and self-adjointness of this kind of Schrödinger operator. Secondly, by using the form approach, we give the necessary and sufficient condition that ensures that the spectra of the self-adjoint Schrödinger operators with δʹ-type conditions are discrete.

We present refined and reversed inequalities for the weighted arithmetic mean–harmonic mean functional inequality. Our approach immediately yields the related operator versions in a simple and fast way. We also give some operator and functional inequalities for three or more arguments. As an application, we obtain a refined upper bound for the relative entropy involving functional arguments.

We carry out an in-depth study of some domination and smoothing properties of linear operators and of their role within the theory of eventually positive operator semigroups. On the one hand, we prove that, on many important function spaces, they imply compactness properties. On the other hand, we show that these conditions can be omitted in a number of Perron–Frobenius type spectral theorems. We furthermore prove a Kreĭn–Rutman type theorem on the existence of positive eigenvectors and eigenfunctionals under certain eventual positivity conditions.

Let ${\mathcal C}[{\mathcal X}]$ be any class of operators on a Banach space ${\mathcal X}$ , and let ${Holo}^{-1}({\mathcal C})$ denote the class of operators A for which there exists a holomorphic function f on a neighbourhood ${\mathcal N}$ of the spectrum σ(A) of A such that f is non-constant on connected components of ${\mathcal N}$ and f(A) lies in ${\mathcal C}$ . Let ${{\mathcal R}[{\mathcal X}]}$ denote the class of Riesz operators in ${{\mathcal B}[{\mathcal X}]}$ . This paper considers perturbation of operators $A\in\Phi_{+}({\mathcal X})\Cup\Phi_{-}({\mathcal X})$ (the class of all upper or lower [semi] Fredholm operators) by commuting operators in $B\in{Holo}^{-1}({\mathcal R}[{\mathcal X}])$ . We prove (amongst other results) that if πB (B) = ∏m i = 1(B − μi ) is Riesz, then there exist decompositions ${\mathcal X}=\oplus_{i=1}^m{{\mathcal X}_i}$ and $B=\oplus_{i=1}^m{B|_{{\mathcal X}_i}}=\oplus_{i=1}^m{B_i}$ such that: (i) If λ ≠ 0, then $\pi_B(A,\lambda)=\prod_{i=1}^m{(A-\lambda\mu_i)^{\alpha_i}} \in\Phi_{+}({\mathcal X})$ (resp., $\in\Phi_{-}({\mathcal X})$ ) if and only if $A-\lambda B_0-\lambda\mu_i\in\Phi_{+}({\mathcal X})$ (resp., $\in\Phi_{-}({\mathcal X})$ ), and (ii) (case λ = 0) $A\in\Phi_{+}({\mathcal X})$ (resp., $\in\Phi_{-}({\mathcal X})$ ) if and only if $A-B_0\in\Phi_{+}({\mathcal X})$ (resp., $\in\Phi_{-}({\mathcal X})$ ), where B 0 = ⊕m i = 1(Bi − μi ); (iii) if $\pi_B(A,\lambda)\in\Phi_{+}({\mathcal X})$ (resp., $\in\Phi_{-}({\mathcal X})$ ) for some λ ≠ 0, then $A-\lambda B\in\Phi_{+}({\mathcal X})$ (resp., $\in\Phi_{-}({\mathcal X})$ ).

In this paper we generalize the notion of the C-numerical range of a matrix to operators in arbitrary tracial von Neumann algebras. For each self-adjoint operator C, the C-numerical range of such an operator is defined; it is a compact, convex subset of ℂ. We explicitly describe the C-numerical ranges of several operators and classes of operators.

In this paper, we study spectral properties and local spectral properties of ∞-complex symmetric operators T. In particular, we prove that if T is an ∞-complex symmetric operator, then T has the decomposition property (δ) if and only if T is decomposable. Moreover, we show that if T and S are ∞-complex symmetric operators, then so is T ⊗ S.

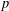
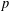
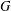
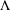
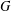
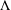
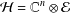
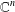
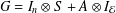
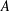
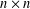
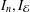
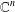
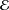
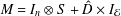
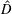
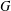
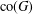
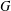
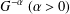
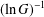
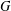
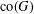
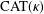
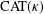
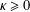
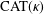
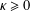
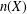
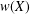
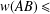
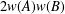
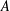
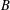
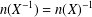
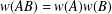
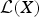
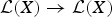
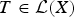
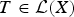
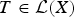
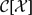
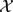
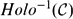
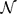
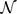
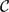
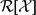
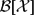
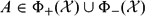
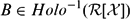
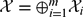
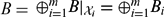
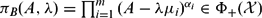
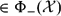
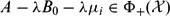
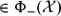
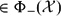
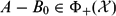
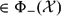
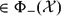
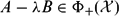
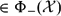
Through appropriate choices of elements in the underlying iterated function system, the methodology of fractal interpolation enables us to associate a family of continuous self-referential functions with a prescribed real-valued continuous function on a real compact interval. This procedure elicits what is referred to as an α-fractal operator on , the space of all real-valued continuous functions defined on a compact interval I. 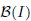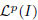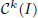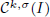With an eye towards connecting fractal functions with other branches of mathematics, in this paper we continue to investigate the fractal operator in more general spaces such as the space of all bounded functions and the Lebesgue space , and in some standard spaces of smooth functions such as the space of k-times continuously differentiable functions, Hölder spaces and Sobolev spaces 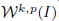. Using properties of the α-fractal operator, the existence of Schauder bases consisting of self-referential functions for these function spaces is established.

We study an M/G/1-type queueing model with the following additional feature. The server works continuously, at fixed speed, even if there are no service requirements. In the latter case, it is building up inventory, which can be interpreted as negative workload. At random times, with an intensity ω(x) when the inventory is at level x>0, the present inventory is removed, instantaneously reducing the inventory to 0. We study the steady-state distribution of the (positive and negative) workload levels for the cases ω(x) is constant and ω(x) = a x. The key tool is the Wiener–Hopf factorization technique. When ω(x) is constant, no specific assumptions will be made on the service requirement distribution. However, in the linear case, we need some algebraic hypotheses concerning the Laplace–Stieltjes transform of the service requirement distribution. Throughout the paper, we also study a closely related model arising from insurance risk theory.

In the spirit of the axiomatic approach by Rogers (1998) we show the equivalence between a set of assumptions on the behaviour of prices and the existence of a representation of these prices as conditional expectations. We rely on only weak assumptions and avoid any a priori modelling of negligible events or of any market filtration. Rather, both endogenously emerge along with the representation as conditional expectations.