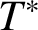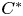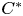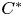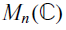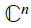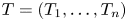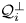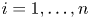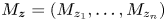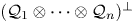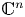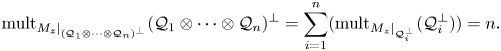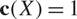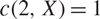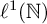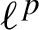Refine listing
Actions for selected content:
292 results in 47Axx
Spectral properties of a beam equation with eigenvalue parameter occurring linearly in the boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 30 July 2021, pp. 780-801
- Print publication:
- June 2022
-
- Article
- Export citation
Wold decomposition on odometer semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 13 July 2021, pp. 738-755
- Print publication:
- June 2022
-
- Article
- Export citation
THE RESOLVENT AND RIESZ TRANSFORM ON CONNECTED SUMS OF MANIFOLDS WITH DIFFERENT ASYMPTOTIC DIMENSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 24 June 2021, pp. 344-345
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
EQUIVALENCE OF SEMI-NORMS RELATED TO SUPER WEAKLY COMPACT OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 506-518
- Print publication:
- December 2021
-
- Article
- Export citation
Operator equalities and Characterizations of Orthogonality in Pre-Hilbert C*-Modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 17 June 2021, pp. 594-614
-
- Article
- Export citation
HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM – II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 376-396
- Print publication:
- May 2022
-
- Article
- Export citation
Chaos and frequent hypercyclicity for composition operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 513-531
-
- Article
- Export citation
Multiplicities, invariant subspaces and an additive formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 279-297
-
- Article
- Export citation
AN UNBOUNDED OPERATOR WITH SPECTRUM IN A STRIP AND MATRIX DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 16 April 2021, pp. 146-153
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
The effects of diffusion on the principal eigenvalue for age-structured models with random diffusion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 258-280
- Print publication:
- February 2022
-
- Article
- Export citation
The polarization constant of finite dimensional complex spaces is one
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 105-123
- Print publication:
- January 2022
-
- Article
- Export citation
Some matrix inequalities of log-majorization type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 95-105
- Print publication:
- March 2022
-
- Article
- Export citation
NONNEGATIVE POLYNOMIALS, SUMS OF SQUARES AND THE MOMENT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 337-341
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
INVERSE OF FREQUENTLY HYPERCYCLIC OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 04 February 2021, pp. 1867-1886
- Print publication:
- November 2022
-
- Article
- Export citation
Bohr phenomenon for operator-valued functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 72-86
-
- Article
- Export citation
Mixing operators with prescribed unimodular eigenvalues
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1-8
- Print publication:
- January 2022
-
- Article
- Export citation
Chaos and frequent hypercyclicity for weighted shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 3634-3670
- Print publication:
- December 2021
-
- Article
- Export citation
The factorisation property of l∞(Xk)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 10 December 2020, pp. 421-448
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
Bloch wave homogenisation of quasiperiodic media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 58-78
-
- Article
- Export citation
SPECTRAL CONDITIONS FOR UNIFORM P-ERGODICITIES OF MARKOV OPERATORS ON ABSTRACT STATES SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 23 September 2020, pp. 682-696
- Print publication:
- September 2021
-
- Article
- Export citation