Published online by Cambridge University Press: 30 July 2021
In this paper, we consider an eigenvalue problem for ordinary differential equations of fourth order with a spectral parameter in the boundary conditions. The location of eigenvalues on real axis, the structure of root subspaces and the oscillation properties of eigenfunctions of this problem are investigated, and asymptotic formulas for the eigenvalues and eigenfunctions are found. Next, by the use of these properties, we establish sufficient conditions for subsystems of root functions of the considered problem to form a basis in the space 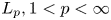 $L_p,1 < p < \infty$.
$L_p,1 < p < \infty$.