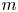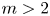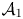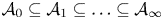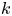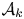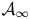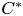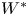1. Introduction
We denote by $\mathbb {Z}_+,$![]() $\mathbb {Z}$
$\mathbb {Z}$![]() and $\mathbb {R}$
and $\mathbb {R}$![]() the sets of non-negative integers, integers and real numbers, respectively. We write $\varOmega ^{*}$
the sets of non-negative integers, integers and real numbers, respectively. We write $\varOmega ^{*}$![]() for the set $\{\bar {z} \colon z \in \varOmega \}$
for the set $\{\bar {z} \colon z \in \varOmega \}$![]() whenever $\varOmega$
whenever $\varOmega$![]() is a subset of the complex plane $\mathbb {C}$
is a subset of the complex plane $\mathbb {C}$![]() . For a positive real number $r,$
. For a positive real number $r,$![]() $\mathbb {D}_r$
$\mathbb {D}_r$![]() stands for the open disc $\{z \in \mathbb {C} \colon |z| < r\}.$
stands for the open disc $\{z \in \mathbb {C} \colon |z| < r\}.$![]() Set $\mathbb {D} := \mathbb {D}_1.$
Set $\mathbb {D} := \mathbb {D}_1.$![]() For positive real numbers $r$
For positive real numbers $r$![]() and $R$
and $R$![]() with $r < R$
with $r < R$![]() , we denote by $\mathbb {A}(r, R)$
, we denote by $\mathbb {A}(r, R)$![]() the annulus $\{z \in \mathbb {C} \colon r < |z| < R\}$
the annulus $\{z \in \mathbb {C} \colon r < |z| < R\}$![]() . We write $\mathbb {R}[x]$
. We write $\mathbb {R}[x]$![]() for the ring of polynomials in one real variable $x$
for the ring of polynomials in one real variable $x$![]() with real coefficients.
with real coefficients.
Unless otherwise stated, all Hilbert spaces appearing below are complex. Let $\mathcal {H}$![]() denote a Hilbert space and let $\mathcal {B}(\mathcal {H})$
denote a Hilbert space and let $\mathcal {B}(\mathcal {H})$![]() stand for the unital $C^*$
stand for the unital $C^*$![]() -algebra of bounded linear operators on $\mathcal {H}$
-algebra of bounded linear operators on $\mathcal {H}$![]() with the identity operator $I$
with the identity operator $I$![]() as the unit. Denote by $[S,T]$
as the unit. Denote by $[S,T]$![]() the commutator $ST-TS$
the commutator $ST-TS$![]() of $S,T \in \mathcal {B}(\mathcal {H}).$
of $S,T \in \mathcal {B}(\mathcal {H}).$![]() The commutator $[S^*, S]$
The commutator $[S^*, S]$![]() is called the self-commutator of $S$
is called the self-commutator of $S$![]() . We write $\ker T$
. We write $\ker T$![]() , ${\mathcal {R}}(T)$
, ${\mathcal {R}}(T)$![]() and $|T|$
and $|T|$![]() for the kernel, the range and the modulus of an operator $T \in \mathcal {B}(\mathcal {H}).$
for the kernel, the range and the modulus of an operator $T \in \mathcal {B}(\mathcal {H}).$![]() The spectrum, the approximate point spectrum and the spectral radius of $T$
The spectrum, the approximate point spectrum and the spectral radius of $T$![]() are denoted by $\sigma (T)$
are denoted by $\sigma (T)$![]() , $\sigma _{ap}(T)$
, $\sigma _{ap}(T)$![]() and $r(T)$
and $r(T)$![]() , respectively.
, respectively.
An operator $T$![]() in $\mathcal {B}(\mathcal {H})$
in $\mathcal {B}(\mathcal {H})$![]() is left-invertible if there exists $L \in \mathcal {B}(\mathcal {H})$
is left-invertible if there exists $L \in \mathcal {B}(\mathcal {H})$![]() (a left-inverse of $T$
(a left-inverse of $T$![]() ) such that $LT=I.$
) such that $LT=I.$![]() Note that $T$
Note that $T$![]() is left-invertible if and only if $0\notin \sigma _{ap}(T)$
is left-invertible if and only if $0\notin \sigma _{ap}(T)$![]() , or equivalently if and only if $T^*T$
, or equivalently if and only if $T^*T$![]() is invertible (as a member of $\mathcal {B}(\mathcal {H})$
is invertible (as a member of $\mathcal {B}(\mathcal {H})$![]() ). Following [Reference Shimorin35], we call the operator $T':=T(T^*T)^{-1}$
). Following [Reference Shimorin35], we call the operator $T':=T(T^*T)^{-1}$![]() the Cauchy dual of $T$
the Cauchy dual of $T$![]() whenever $T$
whenever $T$![]() is left-invertible. For notational brevity, we write $T^{\prime n}$
is left-invertible. For notational brevity, we write $T^{\prime n}$![]() instead of $(T^{\prime })^n,$
instead of $(T^{\prime })^n,$![]() the $n$
the $n$![]() th power of $T^{\prime }$
th power of $T^{\prime }$![]() , when $n$
, when $n$![]() is a non-negative integer (in general, $T^{\prime n}$
is a non-negative integer (in general, $T^{\prime n}$![]() does not coincide with $T^{n\prime }:= (T^n)^{\prime }$
does not coincide with $T^{n\prime }:= (T^n)^{\prime }$![]() ). The Cauchy dual operator provides a canonical choice of a left-inverse $L:=T'^*$
). The Cauchy dual operator provides a canonical choice of a left-inverse $L:=T'^*$![]() for any left-invertible operator $T.$
for any left-invertible operator $T.$![]() We refer the reader to [Reference Shimorin35] for the role that the Cauchy dual operator plays in the solution of the wandering subspace problem for the Bergman shift. Recall that an operator $T \in \mathcal {B}(\mathcal {H})$
We refer the reader to [Reference Shimorin35] for the role that the Cauchy dual operator plays in the solution of the wandering subspace problem for the Bergman shift. Recall that an operator $T \in \mathcal {B}(\mathcal {H})$![]() has the wandering subspace property if
has the wandering subspace property if
We call $T$![]() analytic if $\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^n) =\{0\}.$
analytic if $\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^n) =\{0\}.$![]() Clearly, an analytic operator on a non-zero Hilbert space is never invertible. We say that $T$
Clearly, an analytic operator on a non-zero Hilbert space is never invertible. We say that $T$![]() is concave if
is concave if
The class of concave operators was introduced by Richter [Reference Richter31] on the occasion of investigating invariant subspaces of the Dirichlet shift. The importance of concave operators was emphasized by Richter, who proved that analytic concave operators have the wandering subspace property (see [Reference Richter31, Theorem 1]). In turn, Shimorin proved that concave operators have Wold-type decomposition (see [Reference Shimorin35, Theorem 3.6(A)]). In this paper, we generalize the notion of a concave operator, preserving some of their important properties (see § 3 and 7 for the motivation). The first step generalization refers to weakly concave operators.
Definition 1.1 A left-invertible operator $T \in \mathcal {B}(\mathcal {H})$![]() is said to be weakly concave if it satisfies the following conditions:
is said to be weakly concave if it satisfies the following conditions:
where $\|\cdot \|'$![]() is the norm on $\mathcal {H}$
is the norm on $\mathcal {H}$![]() given by $\|x\|':=\|T'x\|$
given by $\|x\|':=\|T'x\|$![]() for $x \in \mathcal {H}$
for $x \in \mathcal {H}$![]() and $T'$
and $T'$![]() denotes the Cauchy dual of $T$
denotes the Cauchy dual of $T$![]() .
.
Remark 1.2 In view of [Reference Jabłoński and Stochel26, Lemma 3.1] and the inclusion $\partial \sigma (T) \subseteq \sigma _{ap}(T)$![]() (see [Reference Conway17, Proposition VII.6.7]), it is easy to see that, under the assumption (1.2), the condition (1.1) is equivalent to $\sigma (T) \subseteq \overline {\mathbb {D}}$
(see [Reference Conway17, Proposition VII.6.7]), it is easy to see that, under the assumption (1.2), the condition (1.1) is equivalent to $\sigma (T) \subseteq \overline {\mathbb {D}}$![]() (and to $r(T) \leqslant 1$
(and to $r(T) \leqslant 1$![]() ). $\diamondsuit$
). $\diamondsuit$![]()
The following theorem, which is one of the main results of this paper, generalizes [Reference Shimorin35, Theorem 3.6(A)].
Theorem 1.3 Suppose that $T \in \mathcal {B}(\mathcal {H})$![]() is a weakly concave operator. Let $\mathcal {H}_u$
is a weakly concave operator. Let $\mathcal {H}_u$![]() and $\mathcal {H}'_u$
and $\mathcal {H}'_u$![]() denote the closed vector subspaces of $\mathcal {H}$
denote the closed vector subspaces of $\mathcal {H}$![]() given by
given by

Then $\mathcal {H}'_u \subseteq \mathcal {H}_u$![]() and $\mathcal {H}'_u$
and $\mathcal {H}'_u$![]() reduces $T.$
reduces $T.$![]() Moreover,
Moreover,
where $U \in \mathcal {B}(\mathcal {H}'_u)$![]() is unitary and $S \in \mathcal {B}((\mathcal {H}'_u)^{\perp })$
is unitary and $S \in \mathcal {B}((\mathcal {H}'_u)^{\perp })$![]() has the wandering subspace property.
has the wandering subspace property.
In general, the Wold-type decomposition obtained in Theorem 1.3 is weaker than Shimorin's one in the sense that the operator $S$![]() in the decomposition (1.5) of $T$
in the decomposition (1.5) of $T$![]() may not be analytic. However, in the case where $T$
may not be analytic. However, in the case where $T$![]() is concave, it can be seen that $\mathcal {H}'_u=\mathcal {H}_u,$
is concave, it can be seen that $\mathcal {H}'_u=\mathcal {H}_u,$![]() which allows us to recover [Reference Shimorin35, Theorem 3.6(A)] (see Corollary 6.1). The proof of Theorem 1.3 is based on the circle of ideas developed by Shimorin in [Reference Shimorin35] together with the spectral dichotomy principle, which is given in § 5.
which allows us to recover [Reference Shimorin35, Theorem 3.6(A)] (see Corollary 6.1). The proof of Theorem 1.3 is based on the circle of ideas developed by Shimorin in [Reference Shimorin35] together with the spectral dichotomy principle, which is given in § 5.
We also prove the following Berger–Shaw-type theorem together with the Carey–Pincus trace formula for analytic finitely cyclic weakly concave operators (cf. [Reference Conway18, Theorem 2.1, p. 152] and [Reference Chavan12, Proposition 2.21]). Recall that $T\in {\mathcal {B}}(\mathcal {H})$![]() is finitely cyclic if there is a finite dimensional vector subspace $\mathcal {M}$
is finitely cyclic if there is a finite dimensional vector subspace $\mathcal {M}$![]() of $\mathcal {H}$
of $\mathcal {H}$![]() , called a cyclic space of $T$
, called a cyclic space of $T$![]() , such that $\mathcal {H} = \bigvee _{n \in \mathbb {Z}_+} T^n (\mathcal {M}).$
, such that $\mathcal {H} = \bigvee _{n \in \mathbb {Z}_+} T^n (\mathcal {M}).$![]()
Theorem 1.4 Suppose that $T \in \mathcal {B}(\mathcal {H})$![]() is an analytic finitely cyclic weakly concave operator. Then $T$
is an analytic finitely cyclic weakly concave operator. Then $T$![]() and $T'$
and $T'$![]() have trace class self-commutators. Moreover, for any complex polynomials $p, q$
have trace class self-commutators. Moreover, for any complex polynomials $p, q$![]() in two complex variables $z$
in two complex variables $z$![]() and $\bar z$
and $\bar z$![]() ,
,

where $dA$![]() denotes the Lebesgue planar measure.
denotes the Lebesgue planar measure.
The proofs of Theorems 1.3 and 1.4 will be given in § 6.
Remark 1.5 Let $T$![]() be as in Theorem 1.4. Then, in particular, we have
be as in Theorem 1.4. Then, in particular, we have
Further, the Pincus principal function of $T'$![]() is equal to $-\dim \ker T^*$
is equal to $-\dim \ker T^*$![]() times the characteristic function of the open unit disk [see (6.9)]. The reader is referred to [Reference Carey and Pincus11] for the definition of the Pincus principal function. $\diamondsuit$
times the characteristic function of the open unit disk [see (6.9)]. The reader is referred to [Reference Carey and Pincus11] for the definition of the Pincus principal function. $\diamondsuit$![]()
The paper is organized as follows. In § 3, we discuss basic properties of weakly concave operators, including their relation to the theory of hyponormal operators. In § 4, we provide examples of $3$![]() -isometric weakly concave operators which are not concave (see Example 4.5). In § 5, we establish the spectral dichotomy principle for left-invertible operators (see Theorem 5.1). This principle is a key component of the proofs of Theorems 1.3 and 1.4 (see § 6). Both theorems are generalized in Theorems 7.2 and 7.4 to the case of operators of class $\mathcal {A}_k$
-isometric weakly concave operators which are not concave (see Example 4.5). In § 5, we establish the spectral dichotomy principle for left-invertible operators (see Theorem 5.1). This principle is a key component of the proofs of Theorems 1.3 and 1.4 (see § 6). Both theorems are generalized in Theorems 7.2 and 7.4 to the case of operators of class $\mathcal {A}_k$![]() , where $k\in \mathbb {Z}_+ \cup \{\infty \}$
, where $k\in \mathbb {Z}_+ \cup \{\infty \}$![]() (see Definition 7.1). If the underlying Hilbert space is infinite dimensional, then the class $\mathcal {A}_0$
(see Definition 7.1). If the underlying Hilbert space is infinite dimensional, then the class $\mathcal {A}_0$![]() is larger than the class of concave operators, the class $\mathcal {A}_1$
is larger than the class of concave operators, the class $\mathcal {A}_1$![]() consists precisely of weakly concave operators and the sequence $\{\mathcal {A}_k\}_{k=0}^{\infty }$
consists precisely of weakly concave operators and the sequence $\{\mathcal {A}_k\}_{k=0}^{\infty }$![]() is strictly increasing (see Example 7.6). In § 8, we present necessary and sufficient conditions for some restrictions of the Cauchy dual operator of a left-invertible operator to be hyponormal (see Propositions 8.2 and 8.7). Section 9 is devoted to $C^*$
is strictly increasing (see Example 7.6). In § 8, we present necessary and sufficient conditions for some restrictions of the Cauchy dual operator of a left-invertible operator to be hyponormal (see Propositions 8.2 and 8.7). Section 9 is devoted to $C^*$![]() - and $W^*$
- and $W^*$![]() -algebraic analogues of the classes $\mathcal {A}_k.$
-algebraic analogues of the classes $\mathcal {A}_k.$![]()
2. Preliminaries
The left spectrum $\sigma _l(T)$![]() of $T \in \mathcal {B}(\mathcal {H})$
of $T \in \mathcal {B}(\mathcal {H})$![]() is defined as the set of those $\lambda$
is defined as the set of those $\lambda$![]() in $\mathbb {C}$
in $\mathbb {C}$![]() for which $T-\lambda I$
for which $T-\lambda I$![]() is not left-invertible. Similarly, one can define the right spectrum $\sigma _r(T)$
is not left-invertible. Similarly, one can define the right spectrum $\sigma _r(T)$![]() of $T.$
of $T.$![]() It is easy to see that
It is easy to see that
We say that an operator $T \in \mathcal {B}(\mathcal {H})$![]() with closed range is left Fredholm (resp. right Fredholm) if $\dim \ker T< \infty$
with closed range is left Fredholm (resp. right Fredholm) if $\dim \ker T< \infty$![]() (resp. $\dim \ker T^* < \infty$
(resp. $\dim \ker T^* < \infty$![]() ). Operators which are simultaneously left and right Fredholm are called Fredholm operators. The essential spectrum $\sigma _e(T)$
). Operators which are simultaneously left and right Fredholm are called Fredholm operators. The essential spectrum $\sigma _e(T)$![]() of $T$
of $T$![]() is the complement of the set of those $\lambda \in \mathbb {C}$
is the complement of the set of those $\lambda \in \mathbb {C}$![]() for which $T-\lambda I$
for which $T-\lambda I$![]() is Fredholm. The function $\text {ind}_T$
is Fredholm. The function $\text {ind}_T$![]() defined by
defined by
is called the Fredholm index of $T$![]() . Similarly, we define the left essential spectrum $\sigma _{le}(T)$
. Similarly, we define the left essential spectrum $\sigma _{le}(T)$![]() and the right essential spectrum $\sigma _{re}(T)$
and the right essential spectrum $\sigma _{re}(T)$![]() of $T.$
of $T.$![]() We refer the reader to [Reference Conway17] for the foundations of the theory of Fredholm operators.
We refer the reader to [Reference Conway17] for the foundations of the theory of Fredholm operators.
An operator $T$![]() in ${\mathcal {B}}(\mathcal {H})$
in ${\mathcal {B}}(\mathcal {H})$![]() is of trace class if $\|T\|_{1, \mathcal {E}}:= \sum _{n =0}^{\infty }\langle {|T|e_n},\,{e_n} \rangle$
is of trace class if $\|T\|_{1, \mathcal {E}}:= \sum _{n =0}^{\infty }\langle {|T|e_n},\,{e_n} \rangle$![]() is finite for every choice of an orthonormal basis $\mathcal {E}=\{e_n\}_{n \in \mathbb {Z}_+}$
is finite for every choice of an orthonormal basis $\mathcal {E}=\{e_n\}_{n \in \mathbb {Z}_+}$![]() of $\mathcal {H}.$
of $\mathcal {H}.$![]() The number $\|T\|_{1, \mathcal {E}}$
The number $\|T\|_{1, \mathcal {E}}$![]() turns out to be independent of the choice of an orthonormal basis $\mathcal {E}$
turns out to be independent of the choice of an orthonormal basis $\mathcal {E}$![]() of $\mathcal {H}$
of $\mathcal {H}$![]() and is denoted by $\|T\|_1.$
and is denoted by $\|T\|_1.$![]() It is called the trace norm of $T.$
It is called the trace norm of $T.$![]() In case $T$
In case $T$![]() is of trace class, the trace of $T$
is of trace class, the trace of $T$![]() given by $\text {tr}(T) =\sum _{n = 0}^{\infty }\langle {Te_n},\,{e_n} \rangle$
given by $\text {tr}(T) =\sum _{n = 0}^{\infty }\langle {Te_n},\,{e_n} \rangle$![]() is a finite number. Again, it is independent of the choice of an orthonormal basis $\mathcal {E}$
is a finite number. Again, it is independent of the choice of an orthonormal basis $\mathcal {E}$![]() of $\mathcal {H}$
of $\mathcal {H}$![]() (see [Reference Simon39] for more details on trace class operators).
(see [Reference Simon39] for more details on trace class operators).
An operator $T\in \mathcal {B}(\mathcal {H})$![]() is said to be completely non-unitary (resp., completely non-normal) if there is no nonzero closed subspace of $\mathcal {H}$
is said to be completely non-unitary (resp., completely non-normal) if there is no nonzero closed subspace of $\mathcal {H}$![]() reducing $T$
reducing $T$![]() to a unitary (resp., normal) operator. Clearly, if $T \in \mathcal {B}(\mathcal {H})$
to a unitary (resp., normal) operator. Clearly, if $T \in \mathcal {B}(\mathcal {H})$![]() is analytic, then $T$
is analytic, then $T$![]() is completely non-unitary. The following fact is easy to verify.
is completely non-unitary. The following fact is easy to verify.
An operator $T \in \mathcal {B}(\mathcal {H})$![]() is said to be hyponormal if the self-commutator of $T$
is said to be hyponormal if the self-commutator of $T$![]() is positive. The reader is referred to [Reference Conway18, Chapter IV] and [Reference Martin and Putinar28, Chapter 1] for the fundamentals of the theory of hyponormal operators including the statements of Berger–Shaw Theorem and Putnam's inequality. Given a positive integer $m$
is positive. The reader is referred to [Reference Conway18, Chapter IV] and [Reference Martin and Putinar28, Chapter 1] for the fundamentals of the theory of hyponormal operators including the statements of Berger–Shaw Theorem and Putnam's inequality. Given a positive integer $m$![]() and $T \in \mathcal {B}(\mathcal {H})$
and $T \in \mathcal {B}(\mathcal {H})$![]() , we set
, we set

We say that $T$![]() is a contraction (resp. an expansion) if $B_1(T) \geqslant 0$
is a contraction (resp. an expansion) if $B_1(T) \geqslant 0$![]() (resp., ${B_1(T)\leqslant 0}$
(resp., ${B_1(T)\leqslant 0}$![]() ). For an integer $m \geqslant 2$
). For an integer $m \geqslant 2$![]() , an operator $T \in \mathcal {B}(\mathcal {H})$
, an operator $T \in \mathcal {B}(\mathcal {H})$![]() is said to be an $m$
is said to be an $m$![]() -isometry if ${B_m(T) = 0}$
-isometry if ${B_m(T) = 0}$![]() . By a strict $m$
. By a strict $m$![]() -isometry, we understand an $m$
-isometry, we understand an $m$![]() -isometry which is not an $(m-1)$
-isometry which is not an $(m-1)$![]() -isometry (or not an isometry if $m=2$
-isometry (or not an isometry if $m=2$![]() ). It is well known that any concave operator is expansive (see [Reference Richter31, Lemma 1]). Furthermore, the approximate point spectrum of any $m$
). It is well known that any concave operator is expansive (see [Reference Richter31, Lemma 1]). Furthermore, the approximate point spectrum of any $m$![]() -isometry and any concave operator is contained in the unit circle $\partial \mathbb {D}$
-isometry and any concave operator is contained in the unit circle $\partial \mathbb {D}$![]() (see [Reference Agler and Stankus3, Lemma 1.21], [Reference Jabłoński and Stochel26, Lemma 3.1] and [Reference Richter31, Lemma 1]). In particular, the Cauchy dual operator of an $m$
(see [Reference Agler and Stankus3, Lemma 1.21], [Reference Jabłoński and Stochel26, Lemma 3.1] and [Reference Richter31, Lemma 1]). In particular, the Cauchy dual operator of an $m$![]() -isometry or a concave operator is well defined.
-isometry or a concave operator is well defined.
Straightforward computations yield the following properties of the Cauchy dual operator, where in general $P_{\mathcal {M}}$![]() denotes the orthogonal projection of $\mathcal {H}$
denotes the orthogonal projection of $\mathcal {H}$![]() onto a closed vector subspace $\mathcal {M}$
onto a closed vector subspace $\mathcal {M}$![]() of $\mathcal {H}$
of $\mathcal {H}$![]() .
.
Proposition 2.1 If $T\in \mathcal {B}(\mathcal {H})$![]() is left-invertible and $T=U|T|$
is left-invertible and $T=U|T|$![]() is the polar decomposition of $T$
is the polar decomposition of $T$![]() , then
, then
(i) $U=T|T|^{-1}$
 and $|T'|=|T|^{-1},$
and $|T'|=|T|^{-1},$
(ii) $T'= U|T'|$
 is the polar decomposition of $T'$
is the polar decomposition of $T'$ ,
,(iii) $P_{{\mathcal {R}}(T)} = T'T^* = UU^*$
 .
.
3. An invitation to weakly concave operators
As mentioned in Introduction, any concave operator admits a Wold-type decomposition (see [Reference Shimorin35, Theorem 3.6]). Since concave $m$![]() -isometries are necessarily $2$
-isometries are necessarily $2$![]() -isometries (see [Reference Chavan and Curto14, Proposition 4.9]), the above result is insufficient to obtain a Wold-type decomposition for concave strict $m$
-isometries (see [Reference Chavan and Curto14, Proposition 4.9]), the above result is insufficient to obtain a Wold-type decomposition for concave strict $m$![]() -isometries if $m > 2.$
-isometries if $m > 2.$![]() As a first step towards obtaining the Wold-type decomposition for expansive $m$
As a first step towards obtaining the Wold-type decomposition for expansive $m$![]() -isometries, we consider a class of operators containing concave operators and some strict $m$
-isometries, we consider a class of operators containing concave operators and some strict $m$![]() -isometries with $m> 2.$
-isometries with $m> 2.$![]() Furthermore, in view of the fact that the Cauchy dual of an expansive $m$
Furthermore, in view of the fact that the Cauchy dual of an expansive $m$![]() -isometry is not necessarily hyponormal (in contrast to the case of concave operators, see [Reference Shimorin36, p. 294] or [Reference Chavan12, Theorem 2.9]), it is natural to search for a class of left-invertible operators satisfying a hyponormality-like condition. This motivated us to define the notion of weak concavity (see Definition 1.1), which is central to the present article.
-isometry is not necessarily hyponormal (in contrast to the case of concave operators, see [Reference Shimorin36, p. 294] or [Reference Chavan12, Theorem 2.9]), it is natural to search for a class of left-invertible operators satisfying a hyponormality-like condition. This motivated us to define the notion of weak concavity (see Definition 1.1), which is central to the present article.
According to [Reference Richter31, Lemma 1] and Remark 1.2, concave operators satisfy the conditions (1.1) and (1.2). Hence, trying to generalize the concept of concavity, we included them in Definition 1.1. Although at first glance it is unclear why we use the term ‘weakly concave’, the following theorem sheds more light on this by connecting, via Cauchy dual, the theory of weakly concave operators with the theory of hyponormal operators.
Proposition 3.1 Let $T \in \mathcal {B}(\mathcal {H})$![]() be a left-invertible operator. Then the following conditions are equivalent:
be a left-invertible operator. Then the following conditions are equivalent:
(i) $T$
 satisfies (1.3),
satisfies (1.3),(ii) $T(T^*T)^{-1}T^* \leqslant T^*(T^*T)^{-1}T,$

(iii) $P_{{\mathcal {R}}(T)} \leqslant T^*(T^*T)^{-1}T,$

(iv) the restriction of $T'$
 to its range is hyponormal.
to its range is hyponormal.
In particular, any concave operator is weakly concave.
Proof. That the conditions (i)–(iii) are equivalent is immediate from the following identities (see Proposition 2.1):
To see that the conditions (i) and (iv) are equivalent, note that $T'|_{{\mathcal {R}}(T')}$![]() is hyponormal if and only if
is hyponormal if and only if
Using (3.1) and the equalities $(T'|_{{\mathcal {R}}(T')})^* = P_{{\mathcal {R}}(T')}T'^*|_{{\mathcal {R}}(T')}$![]() and ${\mathcal {R}}(T')={\mathcal {R}}(T)$
and ${\mathcal {R}}(T')={\mathcal {R}}(T)$![]() , we conclude that the operator $T'|_{{\mathcal {R}}(T')}$
, we conclude that the operator $T'|_{{\mathcal {R}}(T')}$![]() is hyponormal if and only if
is hyponormal if and only if
The above inequality coincides with (1.3). This shows that the conditions (i)–(iv) are equivalent.
To show the remaining part, recall that any concave operator satisfies (1.1) and (1.2). Since the Cauchy dual of a concave operator is hyponormal (see [Reference Shimorin36, p. 294]) and the restriction of a hyponormal operator to its closed invariant subspace is hyponormal (see [Reference Conway18, Proposition II.4.4]), an application of the implication (iv)$\Rightarrow$![]() (i) completes the proof.
(i) completes the proof.
Our next goal is to show that the only invertible weakly concave operators are unitary operators (cf. Corollary 3.3). In fact, this is a consequence of a much more general fact proved below.
Proposition 3.2 Let $T \in \mathcal {B}(\mathcal {H})$![]() satisfy (1.1) and let $T'|_{\mathcal {H}_u'}$
satisfy (1.1) and let $T'|_{\mathcal {H}_u'}$![]() be hyponormal, where $\mathcal {H}_u':=\bigcap _{n=0}^{\infty } {\mathcal {R}}(T^{\prime n})$
be hyponormal, where $\mathcal {H}_u':=\bigcap _{n=0}^{\infty } {\mathcal {R}}(T^{\prime n})$![]() . Then the following statements are valid:
. Then the following statements are valid:
(i) $T$
 is unitary if $T$
is unitary if $T$ is invertible,
is invertible,(ii) $T$
 is completely non-normal if $T$
is completely non-normal if $T$ is analytic.
is analytic.
Proof. (i) Assume that $T$![]() is invertible. Since $\partial \sigma (T) \subseteq \sigma _{ap}(T)$
is invertible. Since $\partial \sigma (T) \subseteq \sigma _{ap}(T)$![]() , we infer from (1.1) that $\sigma (T) \subseteq \partial \mathbb {D}$
, we infer from (1.1) that $\sigma (T) \subseteq \partial \mathbb {D}$![]() . Hence
. Hence
Noting that the invertibility of $T$![]() implies the invertibility of $T'$
implies the invertibility of $T'$![]() , we deduce that ${\mathcal {H}_u'=\mathcal {H}}$
, we deduce that ${\mathcal {H}_u'=\mathcal {H}}$![]() . From the assumption that $T'|_{\mathcal {H}_u'}$
. From the assumption that $T'|_{\mathcal {H}_u'}$![]() is hyponormal, we see that $T'$
is hyponormal, we see that $T'$![]() is hyponormal. However, by invertibility of $T$
is hyponormal. However, by invertibility of $T$![]() , $T'=T^{*-1},$
, $T'=T^{*-1},$![]() which by [Reference Conway18, Proposition II.4.4] implies that $T^*$
which by [Reference Conway18, Proposition II.4.4] implies that $T^*$![]() is hyponormal. Hence, by (3.2) and the second corollary on [Reference Stampfli40, Pg 473], $T$
is hyponormal. Hence, by (3.2) and the second corollary on [Reference Stampfli40, Pg 473], $T$![]() is unitary.
is unitary.
(ii) Assume now that $T$![]() is analytic. Suppose to the contrary that $T$
is analytic. Suppose to the contrary that $T$![]() has a non-zero normal direct summand, say $N$
has a non-zero normal direct summand, say $N$![]() . Then by (1.1), we have
. Then by (1.1), we have
Hence, $N$![]() is unitary. This contradicts the fact that every analytic operator is completely non-unitary.
is unitary. This contradicts the fact that every analytic operator is completely non-unitary.
The following corollary is immediate from Propositions 3.1 and 3.2 and [Reference Conway18, Proposition II.4.4].
Corollary 3.3 If $T \in \mathcal {B}(\mathcal {H})$![]() is weakly concave, then the following statements are valid:
is weakly concave, then the following statements are valid:
(i) $T$
 is unitary if $T$
is unitary if $T$ is invertible,
is invertible,(ii) $T$
 is completely non-normal if $T$
is completely non-normal if $T$ is analytic.
is analytic.
4. Examples
In this section, we show that there are weakly concave operators which are not concave (see Example 4.5 below). This is done by means of unilateral weighted shifts. Recall that for a bounded sequence $\{w_n\}_{n = 0}^{\infty }$![]() of positive real numbers, there exists a unique operator $W\in \mathcal {B}(\ell ^2)$
of positive real numbers, there exists a unique operator $W\in \mathcal {B}(\ell ^2)$![]() (called a unilateral weighted shift with weight sequence $\{w_n\}_{n = 0}^{\infty }$
(called a unilateral weighted shift with weight sequence $\{w_n\}_{n = 0}^{\infty }$![]() ) such that
) such that
where $\{e_n\}_{n = 0}^{\infty }$![]() stands for the standard orthonormal basis of $\ell ^2,$
stands for the standard orthonormal basis of $\ell ^2,$![]() the Hilbert space of square summable complex sequences indexed by $\mathbb {Z}_+.$
the Hilbert space of square summable complex sequences indexed by $\mathbb {Z}_+.$![]() Note that unilateral weighted shifts are always analytic. Before providing the aforementioned example, we need some auxiliary results. We begin by characterizing those unilateral weighted shifts whose given power is left-invertible and satisfies the condition (1.3).
Note that unilateral weighted shifts are always analytic. Before providing the aforementioned example, we need some auxiliary results. We begin by characterizing those unilateral weighted shifts whose given power is left-invertible and satisfies the condition (1.3).
Proposition 4.1 Let $W$![]() be a unilateral weighted shift with weight sequence $\{w_n\}_{n=0}^{\infty }$
be a unilateral weighted shift with weight sequence $\{w_n\}_{n=0}^{\infty }$![]() and let $k$
and let $k$![]() be a positive integer. Then the following statements are equivalent:
be a positive integer. Then the following statements are equivalent:
(i) $W^k$
 is left-invertible and satisfies (1.3),
is left-invertible and satisfies (1.3),(ii) $\inf _{{n \in \mathbb {Z}_+}}w_{n} > 0$
 and $\prod _{j=0}^{k-1} \frac {w_{n+j}}{w_{k+n+j}} \geqslant 1$
and $\prod _{j=0}^{k-1} \frac {w_{n+j}}{w_{k+n+j}} \geqslant 1$ for every integer $n \geqslant k.$
for every integer $n \geqslant k.$
Proof. First, observe that if $T\in \mathcal {B}(\mathcal {H}),$![]() then for any positive integer $m$
then for any positive integer $m$![]() , $T$
, $T$![]() is left-invertible if and only if $T^m$
is left-invertible if and only if $T^m$![]() is left-invertible. Hence, $W^k$
is left-invertible. Hence, $W^k$![]() is left-invertible if and only if $\inf _{n \in \mathbb {Z}_+} w_n > 0$
is left-invertible if and only if $\inf _{n \in \mathbb {Z}_+} w_n > 0$![]() . This means that there is no loss of generality in assuming that all powers of $W$
. This means that there is no loss of generality in assuming that all powers of $W$![]() are left-invertible. Noting that
are left-invertible. Noting that

we deduce that

Clearly

Combining (4.1) and (4.2) with the equivalence (i) $\Leftrightarrow$![]() (iii) of Proposition 3.1 completes the proof.
(iii) of Proposition 3.1 completes the proof.
The next result we need is closely related to [Reference Anand and Chavan4, Proposition 2.3]. It can be deduced from [Reference Anand, Chavan, Jabłoński and Stochel6, Lemma 3.1] by applying the fact that the (entry-wise) product of Hausdorff moment sequences is a Hausdorff moment sequence (see [Reference Berg, Christensen and Ressel7, p. 179]; see also [Reference Berg, Christensen and Ressel7, § 6.2.4] for the definition of the Hausdorff moment sequence) and by using the fundamental theorem of algebra (see [Reference Hungerford23, Theorem V.3.19]).
Proposition 4.2 Suppose that $p$![]() is a polynomial in one real variable which has only negative real roots and whose leading coefficient is positive. Then $p(n) > 0$
is a polynomial in one real variable which has only negative real roots and whose leading coefficient is positive. Then $p(n) > 0$![]() for all $n\in \mathbb {Z}_+$
for all $n\in \mathbb {Z}_+$![]() and $\{1/p(n)\}_{n=0}^{\infty }$
and $\{1/p(n)\}_{n=0}^{\infty }$![]() is a Hausdorff moment sequence.
is a Hausdorff moment sequence.
The following characterization of weakly concave $m$![]() -isometric unilateral weighted shifts is of independent interest.
-isometric unilateral weighted shifts is of independent interest.
Proposition 4.3 Suppose that $W$![]() is a unilateral weighted shift with weight sequence $\{w_n\}_{n = 0}^{\infty }$
is a unilateral weighted shift with weight sequence $\{w_n\}_{n = 0}^{\infty }$![]() and $m \geqslant 2$
and $m \geqslant 2$![]() . Then the following statements are equivalent:
. Then the following statements are equivalent:
(i) $W$
 is a weakly concave $m$
is a weakly concave $m$ -isometry,
-isometry,(ii) there exists a polynomial $p\in \mathbb {R}[x]$
 of degree at most $m-1$
of degree at most $m-1$ such that
(4.3)\begin{align} p(n) > 0\ and\ w^2_n =\frac{p(n+1)}{p(n)}\ for\ all\ n \in \mathbb{Z}_+, \end{align}
such that
(4.3)\begin{align} p(n) > 0\ and\ w^2_n =\frac{p(n+1)}{p(n)}\ for\ all\ n \in \mathbb{Z}_+, \end{align} (4.4)\begin{align} p(n) \leqslant p(n+1)\ for\ all\ n \in \mathbb{Z}_+, \end{align}
(4.4)\begin{align} p(n) \leqslant p(n+1)\ for\ all\ n \in \mathbb{Z}_+, \end{align} (4.5)\begin{align} p(n)p(n+2) \leqslant p(n+1)^2\ for\ all\ n \in \mathbb{Z}_+\backslash \{0\}. \end{align}
(4.5)\begin{align} p(n)p(n+2) \leqslant p(n+1)^2\ for\ all\ n \in \mathbb{Z}_+\backslash \{0\}. \end{align}
Moreover, if $p$![]() is as in Proposition 4.2, then (4.4) and (4.5) hold.
is as in Proposition 4.2, then (4.4) and (4.5) hold.
Proof. By [Reference Abdullah and Le1, Theorem 2.1] (see also [Reference Jabłoński, Jung and Stochel25, Proposition A.2] and [Reference Bermúdez, Martinón and Negrín8, Theorem 3.4]), $W$![]() is an $m$
is an $m$![]() -isometry if and only if there exists a polynomial $p\in \mathbb {R}[x]$
-isometry if and only if there exists a polynomial $p\in \mathbb {R}[x]$![]() of degree at most $m-1$
of degree at most $m-1$![]() such that (4.3) is valid. Therefore, there is no loss of generality in assuming that $W$
such that (4.3) is valid. Therefore, there is no loss of generality in assuming that $W$![]() is an $m$
is an $m$![]() -isometry with $p\in \mathbb {R}[x]$
-isometry with $p\in \mathbb {R}[x]$![]() of degree at most $m-1$
of degree at most $m-1$![]() that satisfies (4.3). By [Reference Agler and Stankus3, Lemma 1.21], $W$
that satisfies (4.3). By [Reference Agler and Stankus3, Lemma 1.21], $W$![]() satisfies (1.1). Hence $0\notin \sigma _{ap}(W)$
satisfies (1.1). Hence $0\notin \sigma _{ap}(W)$![]() , or equivalently $W$
, or equivalently $W$![]() is left-invertible. Moreover, $W$
is left-invertible. Moreover, $W$![]() is an expansion if and only if $w_n \geqslant 1$
is an expansion if and only if $w_n \geqslant 1$![]() for every $n \in \mathbb {Z}_+$
for every $n \in \mathbb {Z}_+$![]() , or equivalently if and only if (4.4) holds. Hence, applying (4.3) and Proposition 4.1 with $k=1$
, or equivalently if and only if (4.4) holds. Hence, applying (4.3) and Proposition 4.1 with $k=1$![]() , we see that the statements (i) and (ii) are equivalent (the condition (4.5) corresponds to (1.3)).
, we see that the statements (i) and (ii) are equivalent (the condition (4.5) corresponds to (1.3)).
Finally, if $p$![]() is as in Proposition 4.2, then $\{1/p(n)\}_{n=0}^{\infty }$
is as in Proposition 4.2, then $\{1/p(n)\}_{n=0}^{\infty }$![]() is a Hausdorff moment sequence which as such is monotonically decreasing and logarithmically convex [the former is equivalent to (4.4), while the latter implies (4.5)].
is a Hausdorff moment sequence which as such is monotonically decreasing and logarithmically convex [the former is equivalent to (4.4), while the latter implies (4.5)].
We also need the following fact, which was proved for finite systems of operators in [Reference Chavan and Curto14]. For the reader's convenience, we give its short proof below. This result is a generalization of [Reference Sholapurkar and Athavale38, Proposition 3.6(ii)].
Proposition 4.4 [Reference Chavan and Curto14, Proposition 4.9]
Suppose that $T \in \mathcal {B}(\mathcal {H})$![]() is a concave $m$
is a concave $m$![]() -isometry for some $m\geqslant 2$
-isometry for some $m\geqslant 2$![]() . Then $T$
. Then $T$![]() is a $2$
is a $2$![]() -isometry.
-isometry.
Proof. It follows from [Reference Richter31, Lemma 1(b)] that
By [Reference Agler and Stankus3, p. 389] (see also [Reference Jabłoński, Jung and Stochel25, Theorem 3.3]), for every $h \in \mathcal {H}$![]() the expression $\|T^n h\|^2$
the expression $\|T^n h\|^2$![]() is a polynomial inFootnote 1 $n$
is a polynomial inFootnote 1 $n$![]() of degree at most $m-1$
of degree at most $m-1$![]() . Combined with (4.6), this implies that $m \leqslant 2$
. Combined with (4.6), this implies that $m \leqslant 2$![]() , which completes the proof.
, which completes the proof.
We are now ready to construct a class of analytic strict $3$![]() -isometric weakly concave operators. Note that such operators cannot be concave which is immediate from Proposition 4.4.
-isometric weakly concave operators. Note that such operators cannot be concave which is immediate from Proposition 4.4.
Example 4.5 Let $p\in \mathbb {R}[x]$![]() be the polynomial defined by $p(x)=|x+z|^2$
be the polynomial defined by $p(x)=|x+z|^2$![]() for $x\in \mathbb {R}$
for $x\in \mathbb {R}$![]() , where $z=u+iv \in \mathbb {C}$
, where $z=u+iv \in \mathbb {C}$![]() with $u, v \in \mathbb {R}$
with $u, v \in \mathbb {R}$![]() such that $v \neq 0$
such that $v \neq 0$![]() . Since $p$
. Since $p$![]() is of degree $2$
is of degree $2$![]() and $p(n) > 0$
and $p(n) > 0$![]() for all $n\in \mathbb {Z}_+$
for all $n\in \mathbb {Z}_+$![]() , the unilateral weighted shift $W$
, the unilateral weighted shift $W$![]() with weight sequence $\{w_n\}_{n = 0}^{\infty }$
with weight sequence $\{w_n\}_{n = 0}^{\infty }$![]() defined by (4.3) is a $3$
defined by (4.3) is a $3$![]() -isometry (see [Reference Abdullah and Le1, Theorem 2.1] and [Reference Jabłoński, Jung and Stochel25, Proposition A.2]). Note that
-isometry (see [Reference Abdullah and Le1, Theorem 2.1] and [Reference Jabłoński, Jung and Stochel25, Proposition A.2]). Note that
Straightforward computations show that
Combined with (4.7) and Proposition 4.3, this implies that $W$![]() is weakly concave if and only if
is weakly concave if and only if
Since the second inequality in (4.8) is equivalent to
we deduce that if $u \geqslant 0$![]() and $v^2 \leqslant 7/2$
and $v^2 \leqslant 7/2$![]() , then $W$
, then $W$![]() is weakly concave.
is weakly concave.
Assume now that $u \geqslant -\frac {1}{2}.$![]() Although, in view of (4.8), $W$
Although, in view of (4.8), $W$![]() need not be weakly concave, quite surprisingly, $W^k$
need not be weakly concave, quite surprisingly, $W^k$![]() turns out to be weakly concave for sufficiently large $k$
turns out to be weakly concave for sufficiently large $k$![]() . To see this, we can argue as follows. By (4.7), $W$
. To see this, we can argue as follows. By (4.7), $W$![]() is expansive. Since $W$
is expansive. Since $W$![]() is a 3-isometry, it follows from [Reference Jabłoński24, Theorem 2.3] that for every integer $k\geqslant 1,$
is a 3-isometry, it follows from [Reference Jabłoński24, Theorem 2.3] that for every integer $k\geqslant 1,$![]() $W^k$
$W^k$![]() is an expansive $3$
is an expansive $3$![]() -isometry, and so by [Reference Agler and Stankus3, Lemma 1.21], $T = W^k$
-isometry, and so by [Reference Agler and Stankus3, Lemma 1.21], $T = W^k$![]() satisfies (1.1) and (1.2). Observe that the second inequality in the condition (ii) of Proposition 4.1 holds if and only if
satisfies (1.1) and (1.2). Observe that the second inequality in the condition (ii) of Proposition 4.1 holds if and only if
Straightforward computations show that
Now if $k$![]() is any positive integer such that $k^2 \geqslant 2v^2,$
is any positive integer such that $k^2 \geqslant 2v^2,$![]() then the above inequality holds, and so $p$
then the above inequality holds, and so $p$![]() satisfies (4.9). Summarizing, if $u\geqslant -\frac {1}{2}$
satisfies (4.9). Summarizing, if $u\geqslant -\frac {1}{2}$![]() and $k \geqslant \sqrt {2}|v|$
and $k \geqslant \sqrt {2}|v|$![]() , then by Proposition 4.1, $W^k$
, then by Proposition 4.1, $W^k$![]() is a weakly concave $3$
is a weakly concave $3$![]() -isometry. Note that if $k$
-isometry. Note that if $k$![]() is any positive integer, then $W^k$
is any positive integer, then $W^k$![]() is not a $2$
is not a $2$![]() -isometry. This follows from [Reference Jabłoński, Jung and Stochel25, Theorem 3.3] by observing that the identity
-isometry. This follows from [Reference Jabłoński, Jung and Stochel25, Theorem 3.3] by observing that the identity
implies that the expression $\|(W^k)^n e_0\|^2$![]() is a polynomial in $n$
is a polynomial in $n$![]() of degree $2$
of degree $2$![]() (see footnote Footnote 1). Hence, by Proposition 4.4, $W^k$
(see footnote Footnote 1). Hence, by Proposition 4.4, $W^k$![]() is not concave for any positive integer $k$
is not concave for any positive integer $k$![]() . $\diamondsuit$
. $\diamondsuit$![]()
5. A spectral dichotomy
Recall the well-known fact that the spectra of an invertible operator $T \in \mathcal {B}(\mathcal {H})$![]() and its inverse $T^{-1} \in \mathcal {B}(\mathcal {H})$
and its inverse $T^{-1} \in \mathcal {B}(\mathcal {H})$![]() are related to each other and the correspondence is given by
are related to each other and the correspondence is given by
where $\phi (\lambda )=1/\lambda$![]() is an automorphism of the punctured plane $\mathbb {C}_{\bullet }:=\mathbb {C} \backslash \{0\}$
is an automorphism of the punctured plane $\mathbb {C}_{\bullet }:=\mathbb {C} \backslash \{0\}$![]() (see [Reference Simon39, Theorem 2.3.2] for the general version of the spectral mapping theorem). A question worth considering in the context of the present paper is to find the counterpart of this simple fact for left-invertible operators $T$
(see [Reference Simon39, Theorem 2.3.2] for the general version of the spectral mapping theorem). A question worth considering in the context of the present paper is to find the counterpart of this simple fact for left-invertible operators $T$![]() . More specifically, if $L$
. More specifically, if $L$![]() is a left-inverse of $T$
is a left-inverse of $T$![]() , then what is the relationship between the spectra of $T$
, then what is the relationship between the spectra of $T$![]() and $L$
and $L$![]() . The purpose of this section is largely to answer this question. It is worth noting that among the left inverses of a left-invertible operator $T$
. The purpose of this section is largely to answer this question. It is worth noting that among the left inverses of a left-invertible operator $T$![]() there exist such as $T^{\prime *}$
there exist such as $T^{\prime *}$![]() , where $T^{\prime }$
, where $T^{\prime }$![]() is the Cauchy dual of $T$
is the Cauchy dual of $T$![]() (see [Reference Richter30, Proposition 5.1] for concrete examples).
(see [Reference Richter30, Proposition 5.1] for concrete examples).
Before stating the main result of this section, observe that if $T\in \mathcal {B}(\mathcal {H})$![]() is left-invertible and $L\in \mathcal {B}(\mathcal {H})$
is left-invertible and $L\in \mathcal {B}(\mathcal {H})$![]() is a left-inverse of $T$
is a left-inverse of $T$![]() , then
, then
Theorem 5.1 [Spectral dichotomy]
Let $T \in \mathcal {B}(\mathcal {H})$![]() be a left-invertible operator with a left-inverse $L \in \mathcal {B}(\mathcal {H})$
be a left-invertible operator with a left-inverse $L \in \mathcal {B}(\mathcal {H})$![]() . Consider the automorphism $\phi$
. Consider the automorphism $\phi$![]() of the punctured plane $\mathbb {C}_{\bullet }$
of the punctured plane $\mathbb {C}_{\bullet }$![]() given by $\phi (z) = 1/{z}$
given by $\phi (z) = 1/{z}$![]() for $z \in \mathbb {C}_{\bullet },$
for $z \in \mathbb {C}_{\bullet },$![]() and extend it to the Riemann sphere $\mathbb {C} \cup \{\infty \}$
and extend it to the Riemann sphere $\mathbb {C} \cup \{\infty \}$![]() by setting $\phi (0)=\infty$
by setting $\phi (0)=\infty$![]() and $\phi (\infty )=0.$
and $\phi (\infty )=0.$![]() Then
Then
according as $0 \in \sigma (T)$![]() or $0 \notin \sigma (T)$
or $0 \notin \sigma (T)$![]() $($
$($![]() see Fig. 1$)$
see Fig. 1$)$![]() . In any case, $0 \notin \partial \sigma (L)$
. In any case, $0 \notin \partial \sigma (L)$![]() and
and

FIG. 1. The relationship between the spectra of a left-invertible operator $T$![]() and its left-inverse $L,$
and its left-inverse $L,$![]() where ${}^\centerdot$
where ${}^\centerdot$![]() denotes the origin in the complex plane.
denotes the origin in the complex plane.
Proof. We begin by noting that
Second, there is no loss of generality in assuming that $0\in \sigma (T)$![]() (because otherwise $L=T^{-1}$
(because otherwise $L=T^{-1}$![]() , and so we can use (5.1) to get $\phi (\sigma (L)) =\sigma (T)$
, and so we can use (5.1) to get $\phi (\sigma (L)) =\sigma (T)$![]() ). Thus, by (5.2), $L$
). Thus, by (5.2), $L$![]() is not invertible. Since $T$
is not invertible. Since $T$![]() is left-invertible, $T$
is left-invertible, $T$![]() is not right-invertible. In turn, because $L$
is not right-invertible. In turn, because $L$![]() is right-invertible, $L$
is right-invertible, $L$![]() is not left-invertible. This yields
is not left-invertible. This yields
We claim that
For, assume that $\lambda \in \mathbb {C}_{\bullet } {\setminus} \sigma _{l}(L)$![]() . Then there exists $L_1\in \mathcal {B}(\mathcal {H})$
. Then there exists $L_1\in \mathcal {B}(\mathcal {H})$![]() such that
such that
Hence, by (5.5), $T-\lambda ^{-1}I$![]() is left-invertible, meaning that $\lambda ^{-1}\in \mathbb {C} {\setminus} \sigma _{l}(T)$
is left-invertible, meaning that $\lambda ^{-1}\in \mathbb {C} {\setminus} \sigma _{l}(T)$![]() . Thus, to get (5.7), it suffices to show that $\lambda ^{-1} \in \sigma _{r}(T).$
. Thus, to get (5.7), it suffices to show that $\lambda ^{-1} \in \sigma _{r}(T).$![]() Suppose, to the contrary, that $\lambda ^{-1} \in \mathbb {C}{\setminus} \sigma _{r}(T)$
Suppose, to the contrary, that $\lambda ^{-1} \in \mathbb {C}{\setminus} \sigma _{r}(T)$![]() . As a consequence, $T-\lambda ^{-1}I$
. As a consequence, $T-\lambda ^{-1}I$![]() is invertible. Right-multiplying (5.5) by the inverse of $T-\lambda ^{-1}I$
is invertible. Right-multiplying (5.5) by the inverse of $T-\lambda ^{-1}I$![]() yields
yields
Now left-multiplying (5.9) by $L_1$![]() leads to
leads to
Finally, left-multiplying (5.10) by $T - \lambda ^{-1} I$![]() gives
gives
This means that $L$![]() is left-invertible, showing that $0 \in \mathbb {C} \backslash \sigma _{l}(L)$
is left-invertible, showing that $0 \in \mathbb {C} \backslash \sigma _{l}(L)$![]() , which contradicts (5.6). This justifies (5.7). Combined with (5.6), this implies the first inclusion in (5.3).
, which contradicts (5.6). This justifies (5.7). Combined with (5.6), this implies the first inclusion in (5.3).
To prove (5.4), we first check that $0 \notin \partial \sigma (L)$![]() . Note that
. Note that
Next, since $L$![]() is right-invertible and
is right-invertible and
we see that $0 \notin \sigma _{ap}(L^*)$![]() . Combined with (5.11) and $\partial \sigma (L^*) \subseteq \sigma _{ap}(L^*),$
. Combined with (5.11) and $\partial \sigma (L^*) \subseteq \sigma _{ap}(L^*),$![]() this implies that $0 \notin \partial \sigma (L)$
this implies that $0 \notin \partial \sigma (L)$![]() . Since, by (5.7), $\phi (\mathbb {C}_{\bullet } {\setminus} \sigma (L)) \subseteq \sigma _{r}(T) {\setminus} \sigma _{l}(T),$
. Since, by (5.7), $\phi (\mathbb {C}_{\bullet } {\setminus} \sigma (L)) \subseteq \sigma _{r}(T) {\setminus} \sigma _{l}(T),$![]() and the right spectrum of any bounded linear operator is closed, the inclusion $\phi (\partial \sigma (L)) \subseteq \sigma _r(T)$
and the right spectrum of any bounded linear operator is closed, the inclusion $\phi (\partial \sigma (L)) \subseteq \sigma _r(T)$![]() now follows from the continuity of $\phi.$
now follows from the continuity of $\phi.$![]() This completes the proof.
This completes the proof.
Corollary 5.2 Let $T \in \mathcal {B}(\mathcal {H})$![]() be a left-invertible operator with a left-inverse $L \in \mathcal {B}(\mathcal {H})$
be a left-invertible operator with a left-inverse $L \in \mathcal {B}(\mathcal {H})$![]() . Then the spectral radius $r(L)$
. Then the spectral radius $r(L)$![]() of $L$
of $L$![]() is positive and
is positive and
according to $0 \in \sigma (T)$![]() or $0 \notin \sigma (T)$
or $0 \notin \sigma (T)$![]() . In particular, $r(T)r(L) \geqslant 1.$
. In particular, $r(T)r(L) \geqslant 1.$![]()
Proof. By Theorem 5.1, $0 \notin \partial \sigma (L)$![]() and so $r(L) > 0$
and so $r(L) > 0$![]() . According to the definition of the spectral radius, $\mathbb {D}_{1/r(L)} \cap \phi (\sigma (L)) = \emptyset$
. According to the definition of the spectral radius, $\mathbb {D}_{1/r(L)} \cap \phi (\sigma (L)) = \emptyset$![]() , and thus the desired dichotomy is immediate from Theorem 5.1. The inequality $r(T)r(L) \geqslant 1$
, and thus the desired dichotomy is immediate from Theorem 5.1. The inequality $r(T)r(L) \geqslant 1$![]() follows from (5.12).
follows from (5.12).
Remark 5.3 Since $L^nT^n=I$![]() holds for any positive integer $n,$
holds for any positive integer $n,$![]() one may derive $r(T)r(L) \geqslant 1$
one may derive $r(T)r(L) \geqslant 1$![]() also from the Gelfand spectral radius formula. $\diamondsuit$
also from the Gelfand spectral radius formula. $\diamondsuit$![]()
Note that if $T\in \mathcal {B}(\mathcal {H})$![]() is a left-invertible operator, then by Theorem 5.1 applied to the left-inverse $L=T^{\prime *}$
is a left-invertible operator, then by Theorem 5.1 applied to the left-inverse $L=T^{\prime *}$![]() of $T$
of $T$![]() , we get
, we get
In general, the above inclusion is strict. We discuss this in more detail in the context of unilateral weighted shifts. Before that, we introduce the necessary notation. For $T \in \mathcal {B}(\mathcal {H})$![]() , we set $i(T):= \lim _{n \to \infty } (\inf _{\|x\|=1}\|T^nx\|)^{1/n}.$
, we set $i(T):= \lim _{n \to \infty } (\inf _{\|x\|=1}\|T^nx\|)^{1/n}.$![]() Clearly, $i(T) \leqslant r(T)$
Clearly, $i(T) \leqslant r(T)$![]() . Moreover, by [Reference Shields37, Proposition 13], we have
. Moreover, by [Reference Shields37, Proposition 13], we have
Example 5.4 Let $W\in \mathcal {B}(\ell ^2)$![]() be a left-invertible unilateral weighted shift with positive weights $\{w_n\}_{n=0}^{\infty }$
be a left-invertible unilateral weighted shift with positive weights $\{w_n\}_{n=0}^{\infty }$![]() . Then $W',$
. Then $W',$![]() the Cauchy dual of $W,$
the Cauchy dual of $W,$![]() is a left-invertible unilateral weighted shift with weights $\{w_n^{-1}\}_{n=0}^{\infty }$
is a left-invertible unilateral weighted shift with weights $\{w_n^{-1}\}_{n=0}^{\infty }$![]() . As a consequence of [Reference Ridge32, Theorem 6] and [Reference Shields37, Theorem 4], we get
. As a consequence of [Reference Ridge32, Theorem 6] and [Reference Shields37, Theorem 4], we get
In turn, [Reference Ridge32, Theorem 1] implies that $\sigma _l(W)=\overline {\mathbb {A}(i(W), r(W))}$![]() . Since
. Since
and $0\in \sigma (W)$![]() , we deduce from (5.14) that the condition (5.13) takes the following form
, we deduce from (5.14) that the condition (5.13) takes the following form
If we assume that equality holds in the above inclusion, then $\frac {1}{r(W^{\prime })}=i(W),$![]() which is not true in general (see e.g., [Reference Chavan and Trivedi15, Example 2], where $r(W^{\prime })= 2$
which is not true in general (see e.g., [Reference Chavan and Trivedi15, Example 2], where $r(W^{\prime })= 2$![]() and $i(W) \geqslant 2^{-3/4}$
and $i(W) \geqslant 2^{-3/4}$![]() ). $\diamondsuit$
). $\diamondsuit$![]()
We conclude this section with some applications of Theorem 5.1 to the theory of Cauchy dual operators.
Corollary 5.5 Let $T \in \mathcal {B}(\mathcal {H})$![]() be a left-invertible operator such that $0 \in \sigma (T)$
be a left-invertible operator such that $0 \in \sigma (T)$![]() and let $T'$
and let $T'$![]() be the Cauchy dual of $T.$
be the Cauchy dual of $T.$![]() Then the following assertions hold:
Then the following assertions hold:
(i) if $\sigma _r(T') \subseteq \overline {\mathbb {D}},$
 then ${\mathbb {D}} \subseteq \sigma _r(T){\setminus} \sigma _l(T),$
then ${\mathbb {D}} \subseteq \sigma _r(T){\setminus} \sigma _l(T),$
(ii) if $T$
 is a contraction such that $\sigma _r(T')\subseteq \overline {\mathbb {D}}$
is a contraction such that $\sigma _r(T')\subseteq \overline {\mathbb {D}}$ , then $\sigma _r(T)=\sigma (T)=\overline {\mathbb {D}}$
, then $\sigma _r(T)=\sigma (T)=\overline {\mathbb {D}}$ .
.
Proof. (i) Suppose that $\sigma _r(T') \subseteq \overline {\mathbb {D}}$![]() . Set $L=T^{\prime *}$
. Set $L=T^{\prime *}$![]() . Then $L$
. Then $L$![]() is a left-inverse of $T$
is a left-inverse of $T$![]() and
and
This combined with Theorem 5.1 yields
which justifies (i).
(ii) Assume now that $\|T\| \leqslant 1$![]() and $\sigma _r(T') \subseteq \overline {\mathbb {D}}$
and $\sigma _r(T') \subseteq \overline {\mathbb {D}}$![]() . Then using (i) and the well-known fact that the spectral radius of a bounded linear operator is at most its operator norm, we get
. Then using (i) and the well-known fact that the spectral radius of a bounded linear operator is at most its operator norm, we get
Since $\sigma _r(T)$![]() and $\sigma (T)$
and $\sigma (T)$![]() are closed subsets of $\mathbb {C}$
are closed subsets of $\mathbb {C}$![]() , the proof is complete.
, the proof is complete.
Remark 5.6 It is well known and easy to prove that the Cauchy dual $T'$![]() of $T$
of $T$![]() is left-invertible and $(T')'=T.$
is left-invertible and $(T')'=T.$![]() This together with (5.2) implies that $0 \in \sigma (T)$
This together with (5.2) implies that $0 \in \sigma (T)$![]() if and only if $0 \in \sigma (T').$
if and only if $0 \in \sigma (T').$![]() In particular, the roles of $T$
In particular, the roles of $T$![]() and $T'$
and $T'$![]() in Corollary 5.5 can be interchanged. $\diamondsuit$
in Corollary 5.5 can be interchanged. $\diamondsuit$![]()
A solution of the wandering subspace problem for concave operators given by Richter in [Reference Richter31] can also be obtained from the computations of the spectra of the Cauchy dual operators (see [Reference Chavan12, Lemma 2.14]). In turn, these computations can be derived from the Bunce result (see [Reference Conway18, Chapter II, $\S$![]() 12]) on the existence of a rich supply of non-zero $*$
12]) on the existence of a rich supply of non-zero $*$![]() -homomorphisms of the $C^*$
-homomorphisms of the $C^*$![]() -algebra generated by a hyponormal operator (see the proof of [Reference Chavan12, Lemma 2.14]). Interestingly, the following fact, which plays an important role in the proofs of Theorems 1.3 and 1.4, and which generalizes [Reference Chavan12, Lemma 2.14(ii)], can be deduced from the spectral dichotomy.
-algebra generated by a hyponormal operator (see the proof of [Reference Chavan12, Lemma 2.14]). Interestingly, the following fact, which plays an important role in the proofs of Theorems 1.3 and 1.4, and which generalizes [Reference Chavan12, Lemma 2.14(ii)], can be deduced from the spectral dichotomy.
Corollary 5.7 Let $T \in {\mathcal {B}}(\mathcal {H})$![]() be a non-invertible expansion such that $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$
be a non-invertible expansion such that $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$![]() and let $T'$
and let $T'$![]() be the Cauchy dual of $T.$
be the Cauchy dual of $T.$![]() Then
Then
(i) $\sigma (T) = \overline {\mathbb {D}} = \sigma (T')$
 ,
,(ii) $\sigma _{ap}(T) = \partial {\mathbb {D}} =\sigma _{ap}(T')$
 .
.
Proof. Recall the fact that for Hilbert space operators, left spectrum and approximate point spectrum coincide. Note that $T'$![]() is a contraction because $T$
is a contraction because $T$![]() is an expansion. Further, since $T$
is an expansion. Further, since $T$![]() is not invertible, $T'$
is not invertible, $T'$![]() is not invertible. Also, because the boundary of the spectrum is contained in the approximate point spectrum and $0 \in \sigma (T),$
is not invertible. Also, because the boundary of the spectrum is contained in the approximate point spectrum and $0 \in \sigma (T),$![]() we infer from $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$
we infer from $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$![]() that $\sigma (T) = \overline {\mathbb {D}}$
that $\sigma (T) = \overline {\mathbb {D}}$![]() and $\sigma _{ap}(T)=\partial \mathbb {D}.$
and $\sigma _{ap}(T)=\partial \mathbb {D}.$![]() By applying Corollary 5.5(ii) to $T'$
By applying Corollary 5.5(ii) to $T'$![]() , we obtain $\sigma (T')=\overline {\mathbb {D}}$
, we obtain $\sigma (T')=\overline {\mathbb {D}}$![]() and $\partial \mathbb {D} \subseteq \sigma _{ap}(T')$
and $\partial \mathbb {D} \subseteq \sigma _{ap}(T')$![]() (see Remark 5.6). An application of Corollary 5.5(i) to $T'$
(see Remark 5.6). An application of Corollary 5.5(i) to $T'$![]() yields
yields
and hence $\sigma _{ap}(T')=\partial \mathbb {D}$![]() . This completes the proof.
. This completes the proof.
6. Proofs of Theorems 1.3 and 1.4
The proof of Theorem 1.3 is based on a technique developed in [Reference Shimorin35].
Proof of Theorem 1.3 In view of Corollary 3.3(i), we may assume that $0 \in \sigma (T).$![]() Since the subspace $\mathcal {H}'_u$
Since the subspace $\mathcal {H}'_u$![]() [see (1.4)] is invariant for $T'$
[see (1.4)] is invariant for $T'$![]() , we can consider the operator $R:=T'|_{\mathcal {H}'_u} \in \mathcal {B} (\mathcal {H}'_u).$
, we can consider the operator $R:=T'|_{\mathcal {H}'_u} \in \mathcal {B} (\mathcal {H}'_u).$![]() Note that $T'$
Note that $T'$![]() is bounded from below and $R$
is bounded from below and $R$![]() maps $\mathcal {H}'_u$
maps $\mathcal {H}'_u$![]() onto $\mathcal {H}'_u$
onto $\mathcal {H}'_u$![]() , hence $R$
, hence $R$![]() is invertible. By Corollary 5.7(ii), we have
is invertible. By Corollary 5.7(ii), we have
Since $0 \notin \sigma (R)$![]() and $\partial \sigma (R) \subseteq \sigma _{ap}(R)$
and $\partial \sigma (R) \subseteq \sigma _{ap}(R)$![]() , we deduce from (6.1) that $\sigma (R) \subseteq \partial \mathbb {D}.$
, we deduce from (6.1) that $\sigma (R) \subseteq \partial \mathbb {D}.$![]() Further, by Proposition 3.1, $R$
Further, by Proposition 3.1, $R$![]() being a restriction of the hyponormal operator $T'|_{{\mathcal {R}}(T')}$
being a restriction of the hyponormal operator $T'|_{{\mathcal {R}}(T')}$![]() to $\mathcal {H}'_u$
to $\mathcal {H}'_u$![]() is hyponormal. Hence, by [Reference Stampfli40, second corollary, p. 473], $R$
is hyponormal. Hence, by [Reference Stampfli40, second corollary, p. 473], $R$![]() is unitary. Recall that if $\mathcal {M}$
is unitary. Recall that if $\mathcal {M}$![]() is a closed invariant subspace for a contraction $A \in \mathcal {B}(\mathcal {H})$
is a closed invariant subspace for a contraction $A \in \mathcal {B}(\mathcal {H})$![]() such that $A|_{\mathcal {M}}$
such that $A|_{\mathcal {M}}$![]() is unitary, then $\mathcal {M}$
is unitary, then $\mathcal {M}$![]() reduces $A$
reduces $A$![]() (see e.g., [Reference Chavan13, Lemma 2.5]). Applying this fact to $A=T'$
(see e.g., [Reference Chavan13, Lemma 2.5]). Applying this fact to $A=T'$![]() ($T'$
($T'$![]() is a contraction because $T$
is a contraction because $T$![]() is an expansion) and $\mathcal {M}=\mathcal {H}'_u,$
is an expansion) and $\mathcal {M}=\mathcal {H}'_u,$![]() we deduce that $\mathcal {H}'_u$
we deduce that $\mathcal {H}'_u$![]() reduces $T'$
reduces $T'$![]() . By [Reference Anand, Chavan, Jabłoński and Stochel6, Proposition 2.2] applied to $T^{\prime }$
. By [Reference Anand, Chavan, Jabłoński and Stochel6, Proposition 2.2] applied to $T^{\prime }$![]() , $\mathcal {H}'_u$
, $\mathcal {H}'_u$![]() reduces $T$
reduces $T$![]() and $T|_{\mathcal {H}'_u} = R^{\prime }$
and $T|_{\mathcal {H}'_u} = R^{\prime }$![]() . Consequently, $T|_{\mathcal {H}'_u}$
. Consequently, $T|_{\mathcal {H}'_u}$![]() is unitary and so $T(\mathcal {H}'_u)=\mathcal {H}'_u.$
is unitary and so $T(\mathcal {H}'_u)=\mathcal {H}'_u.$![]() This in turn implies that $\mathcal {H}'_u \subseteq \mathcal {H}_u$
This in turn implies that $\mathcal {H}'_u \subseteq \mathcal {H}_u$![]() (see (1.4)). On the other hand, by [Reference Shimorin35, Proposition 2.7(i)] we have
(see (1.4)). On the other hand, by [Reference Shimorin35, Proposition 2.7(i)] we have
Since $T|_{\mathcal {H}'_u}$![]() is unitary, we conclude that $T|_{\mathcal {H} \ominus \mathcal {H}'_u}$
is unitary, we conclude that $T|_{\mathcal {H} \ominus \mathcal {H}'_u}$![]() has the wandering subspace property. This completes the proof.
has the wandering subspace property. This completes the proof.
Corollary 6.1 [Reference Shimorin35, Theorem 3.6(A)]
If $T \in \mathcal {B}(\mathcal {H})$![]() is a concave operator, then $T$
is a concave operator, then $T$![]() has the Wold-type decomposition, that is, $\mathcal {H}_{u}$
has the Wold-type decomposition, that is, $\mathcal {H}_{u}$![]() reduces $T$
reduces $T$![]() , $T|_{\mathcal {H}_{u}}$
, $T|_{\mathcal {H}_{u}}$![]() is unitary and
is unitary and
where $\mathcal {H}_u$![]() is as in (1.4).
is as in (1.4).
Proof. It follows from [Reference Shimorin35, Proposition 3.4] that $\mathcal {H}_u$![]() reduces $T$
reduces $T$![]() to a unitary operator, so by (2.1) and Theorem 1.3 we conclude that $\mathcal {H}_u = \mathcal {H}'_u$
to a unitary operator, so by (2.1) and Theorem 1.3 we conclude that $\mathcal {H}_u = \mathcal {H}'_u$![]() , which completes the proof.
, which completes the proof.
Corollary 6.2 Any weakly concave operator $T \in \mathcal {B}(\mathcal {H})$![]() which is analytic has the Wold-type decomposition.
which is analytic has the Wold-type decomposition.
Before proving the next lemma needed in the proof of Theorem 1.4, we state the following fact (see [Reference Herrero22, Proposition 1(i)] and [Reference Anand, Chavan, Jabłoński and Stochel5, Lemma 3.6]).
Lemma 6.3 Suppose that $T \in \mathcal {B}(\mathcal {H})$![]() is a finitely cyclic operator. Then
is a finitely cyclic operator. Then
Proof. Suppose that $\lambda \in \mathbb {C} {\setminus} \sigma _{ap}(T)$![]() . Then $T-\lambda I$
. Then $T-\lambda I$![]() is left-invertible, so the space ${\mathcal {R}}(T-\lambda I)$
is left-invertible, so the space ${\mathcal {R}}(T-\lambda I)$![]() is closed and $\dim \ker (T-\lambda I)=0$
is closed and $\dim \ker (T-\lambda I)=0$![]() . According to (6.2), $\dim \ker (T^*-\bar \lambda I)< \infty$
. According to (6.2), $\dim \ker (T^*-\bar \lambda I)< \infty$![]() . This means that the operator $T-\lambda I$
. This means that the operator $T-\lambda I$![]() is Fredholm, so $\lambda \in \mathbb {C}{\setminus} \sigma _{e}(T).$
is Fredholm, so $\lambda \in \mathbb {C}{\setminus} \sigma _{e}(T).$![]() This proves (6.3). Moreover, we have
This proves (6.3). Moreover, we have
This completes the proof.
Proof of Theorem 1.4 By (6.2), $\ker T^*$![]() is finite dimensional. Combined with [Reference Shimorin35, Proposition 2.7(ii)] and the hypothesis that $T$
is finite dimensional. Combined with [Reference Shimorin35, Proposition 2.7(ii)] and the hypothesis that $T$![]() is analytic, this implies that $T'$
is analytic, this implies that $T'$![]() is finitely cyclic with the cyclic space $\ker T^*$
is finitely cyclic with the cyclic space $\ker T^*$![]() . Moreover, since the range of $T'$
. Moreover, since the range of $T'$![]() is closed, we have
is closed, we have
It follows that $T'|_{{\mathcal {R}}(T')}$![]() is finitely cyclic with the cyclic space $T'(\ker T^*)$
is finitely cyclic with the cyclic space $T'(\ker T^*)$![]() . By Proposition 3.1, $T'|_{{\mathcal {R}}(T')}$
. By Proposition 3.1, $T'|_{{\mathcal {R}}(T')}$![]() is hyponormal. Hence, by the Berger–Shaw Theorem (see [Reference Conway18, Theorem IV.2.1]), $T'|_{{\mathcal {R}}(T')}$
is hyponormal. Hence, by the Berger–Shaw Theorem (see [Reference Conway18, Theorem IV.2.1]), $T'|_{{\mathcal {R}}(T')}$![]() has a trace class self-commutator. Since $T'$
has a trace class self-commutator. Since $T'$![]() is a finite rank perturbation of $T'|_{{\mathcal {R}}(T')} \oplus 0$
is a finite rank perturbation of $T'|_{{\mathcal {R}}(T')} \oplus 0$![]() , where $0$
, where $0$![]() is the zero operator on $\ker {T^{\prime *}} = \ker {T^*}$
is the zero operator on $\ker {T^{\prime *}} = \ker {T^*}$![]() , and the set of finite rank operators is a $*$
, and the set of finite rank operators is a $*$![]() -ideal, one can see that $T'$
-ideal, one can see that $T'$![]() has a trace class self-commutator. Observing that for any left-invertible operator $A \in \mathcal {B}(\mathcal {H})$
has a trace class self-commutator. Observing that for any left-invertible operator $A \in \mathcal {B}(\mathcal {H})$![]() the following operator identities hold (cf. the proof of [Reference Chavan12, Proposition 2.21]):
the following operator identities hold (cf. the proof of [Reference Chavan12, Proposition 2.21]):

where $P$![]() denotes the orthogonal projection of $\mathcal {H}$
denotes the orthogonal projection of $\mathcal {H}$![]() onto $\ker A^*,$
onto $\ker A^*,$![]() and using the fact that the set of trace class operators is an ideal (see [Reference Simon39, Theorem 3.6.6]), we deduce that $T$
and using the fact that the set of trace class operators is an ideal (see [Reference Simon39, Theorem 3.6.6]), we deduce that $T$![]() has a trace class self-commutator.
has a trace class self-commutator.
To prove the ‘moreover’ part we proceed as follows. First, we show that
Since $T$![]() is analytic, we see that $0\in \sigma (T)$
is analytic, we see that $0\in \sigma (T)$![]() . In view of the above discussion, $T$
. In view of the above discussion, $T$![]() and $T'$
and $T'$![]() are finitely cyclic. Let $S$
are finitely cyclic. Let $S$![]() be any of the operators $T$
be any of the operators $T$![]() or $T'.$
or $T'.$![]() It follows from Corollary 5.7 and Lemma 6.3 that $\sigma (S)=\overline {\mathbb {D}}$
It follows from Corollary 5.7 and Lemma 6.3 that $\sigma (S)=\overline {\mathbb {D}}$![]() and $\sigma _{e}(S) \subseteq \sigma _{ap}(S)=\partial {\mathbb {D}}$
and $\sigma _{e}(S) \subseteq \sigma _{ap}(S)=\partial {\mathbb {D}}$![]() . However, if $\lambda \in \partial {\mathbb {D}}=\partial \sigma (S)$
. However, if $\lambda \in \partial {\mathbb {D}}=\partial \sigma (S)$![]() , then by [Reference Conway17, Theorem XI.6.8] either $\lambda$
, then by [Reference Conway17, Theorem XI.6.8] either $\lambda$![]() is an isolated point of $\sigma (S)$
is an isolated point of $\sigma (S)$![]() (which is not the case) or $\lambda \in \sigma _{e}(S)$
(which is not the case) or $\lambda \in \sigma _{e}(S)$![]() , meaning that $\partial {\mathbb {D}} \subseteq \sigma _{e}(S)$
, meaning that $\partial {\mathbb {D}} \subseteq \sigma _{e}(S)$![]() . Putting all this together, we conclude that $\sigma _{e}(S) = \sigma _{ap}(S) =\partial \mathbb {D}$
. Putting all this together, we conclude that $\sigma _{e}(S) = \sigma _{ap}(S) =\partial \mathbb {D}$![]() , which completes the proof of (6.7).
, which completes the proof of (6.7).
Next, applying (6.7) and the fact that $\mathrm {ind}_S(\cdot )$![]() is constant on connected components of $\mathbb {C} \backslash \sigma _{e}(S)$
is constant on connected components of $\mathbb {C} \backslash \sigma _{e}(S)$![]() (use [Reference Conway17, Corollary XI.3.13]), we deduce that
(use [Reference Conway17, Corollary XI.3.13]), we deduce that

It follows from [Reference Carey and Pincus11, Theorem 8.1] that for any $\lambda \in \mathbb {C} \backslash \sigma _{e}(S)$![]() , the Pincus principal function $\mathcal {P}_S(\cdot )$
, the Pincus principal function $\mathcal {P}_S(\cdot )$![]() of a completely non-normal operator $S$
of a completely non-normal operator $S$![]() with a trace class self-commutator is equal to $\mathrm {ind}_{S}(\lambda )$
with a trace class self-commutator is equal to $\mathrm {ind}_{S}(\lambda )$![]() a.e. with respect to the planar Lebesgue measure in a neighbourhood of $\lambda$
a.e. with respect to the planar Lebesgue measure in a neighbourhood of $\lambda$![]() . By Corollary 3.3(ii) and [Reference Anand, Chavan, Jabłoński and Stochel6, Proposition 2.2], $T$
. By Corollary 3.3(ii) and [Reference Anand, Chavan, Jabłoński and Stochel6, Proposition 2.2], $T$![]() and $T'$
and $T'$![]() are completely non-normal, and thus by (6.7) and (6.8), we deduce that
are completely non-normal, and thus by (6.7) and (6.8), we deduce that
where $\chi _{\mathbb {D}}$![]() stands for the characteristic function of $\mathbb {D}$
stands for the characteristic function of $\mathbb {D}$![]() . Since the Carey–Pincus trace formula for polynomials in $S$
. Since the Carey–Pincus trace formula for polynomials in $S$![]() and $S^*$
and $S^*$![]() is valid for completely non-normal operators $S$
is valid for completely non-normal operators $S$![]() with a trace class self-commutator (see [Reference Carey and Pincus11, Theorem 5.1]; see also [Reference Helton and Howe21, Theorem, p. 148]), the proof is complete.
with a trace class self-commutator (see [Reference Carey and Pincus11, Theorem 5.1]; see also [Reference Helton and Howe21, Theorem, p. 148]), the proof is complete.
The following is a corollary from the proof of Theorem 1.4.
Corollary 6.4 Suppose that $\mathcal {H}\neq \{0\}$![]() and $T \in \mathcal {B}(\mathcal {H})$
and $T \in \mathcal {B}(\mathcal {H})$![]() is an analytic finitely cyclic operator satisfying the conditions (1.1) and (1.2) of Definition 1.1. Then
is an analytic finitely cyclic operator satisfying the conditions (1.1) and (1.2) of Definition 1.1. Then
Moreover, $\dim \ker (T^*)$![]() is a positive integer and
is a positive integer and

Proof. A careful look at [Reference Conway17, Theorem XI.6.8] and the proofs of (6.7) and (6.8) yields (6.10) and (6.11). That $\dim \ker (T^*)$![]() is a positive integer can be inferred from (6.10), (6.11) and the fact that the Fredholm index $\mathrm {ind}_S(\cdot )$
is a positive integer can be inferred from (6.10), (6.11) and the fact that the Fredholm index $\mathrm {ind}_S(\cdot )$![]() of any $S\in \mathcal {B}(\mathcal {H})$
of any $S\in \mathcal {B}(\mathcal {H})$![]() is constant on connected components of $\mathbb {C}\backslash \sigma _{e}(S).$
is constant on connected components of $\mathbb {C}\backslash \sigma _{e}(S).$![]()
Remark 6.5 Let us mention that the identity $\sigma _{e}(S) =\partial \mathbb {D}$![]() which appears in (6.7) can be proved without using [Reference Conway17, Theorem XI.6.8]. Indeed, as in the proof of (6.7), we see that $\sigma _{e}(S) \subseteq \sigma _{ap}(S) = \partial {\mathbb {D}}$
which appears in (6.7) can be proved without using [Reference Conway17, Theorem XI.6.8]. Indeed, as in the proof of (6.7), we see that $\sigma _{e}(S) \subseteq \sigma _{ap}(S) = \partial {\mathbb {D}}$![]() , where $S \in \{T,T'\}$
, where $S \in \{T,T'\}$![]() . Suppose, to the contrary, that $\sigma _{e}(S)$
. Suppose, to the contrary, that $\sigma _{e}(S)$![]() is a proper subset of $\partial {\mathbb {D}}$
is a proper subset of $\partial {\mathbb {D}}$![]() . Then
. Then
Since, in general, $\mathrm {ind}_S(\cdot )$![]() is constant on connected components of $\mathbb {C} {\setminus} \sigma _{e}(S)$
is constant on connected components of $\mathbb {C} {\setminus} \sigma _{e}(S)$![]() , and in our case $\mathbb {C} {\setminus} \sigma _{e}(S)$
, and in our case $\mathbb {C} {\setminus} \sigma _{e}(S)$![]() is connected, by Corollary 5.7(i), $\mathrm {ind}_{S}(\lambda )=0$
is connected, by Corollary 5.7(i), $\mathrm {ind}_{S}(\lambda )=0$![]() whenever $\lambda \in \mathbb {C} {\setminus} \overline {\mathbb {D}}$
whenever $\lambda \in \mathbb {C} {\setminus} \overline {\mathbb {D}}$![]() . We conclude that (recall that $\dim \ker T^* = \dim \ker T^{\prime *}$
. We conclude that (recall that $\dim \ker T^* = \dim \ker T^{\prime *}$![]() )
)
This implies that $T$![]() is invertible, which contradicts $0\in \sigma (T)$
is invertible, which contradicts $0\in \sigma (T)$![]() . $\diamondsuit$
. $\diamondsuit$![]()
7. Generalizations to the classes $\mathcal {A}_{k}$
Motivated by the study of weakly concave operators, we introduce and discuss the following related classes of operators.
Definition 7.1 Let $T\in \mathcal {B}(\mathcal {H})$![]() . We say that $T$
. We say that $T$![]() is of class $\mathcal {A}_{\infty }$
is of class $\mathcal {A}_{\infty }$![]() if
if
(i) $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$
 ,
,(ii) $T$
 is an expansion,
is an expansion,(iii∞) $T'|_{\mathcal {H}_u'}$
 is hyponormal with $\mathcal {H}_u'=\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^{\prime n})$
is hyponormal with $\mathcal {H}_u'=\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^{\prime n})$ .
.
Given $k \in \mathbb {Z}_+,$![]() we say that $T$
we say that $T$![]() is of class $\mathcal {A}_{k}$
is of class $\mathcal {A}_{k}$![]() if (i), (ii) and (iii$_{k}$
if (i), (ii) and (iii$_{k}$![]() ) hold, where
) hold, where
(iiik) $T'|_{{\mathcal {R}}(T'^k)}$
 is hyponormal.
is hyponormal.
It follows from [Reference Shimorin36, p. 294] and Proposition 3.1 that the class $\mathcal {A}_0$![]() contains all concave operators and the class $\mathcal {A}_1$
contains all concave operators and the class $\mathcal {A}_1$![]() consists exactly of weakly concave operators. Since the restriction of a hyponormal operator to its closed invariant subspace is again hyponormal, we conclude that
consists exactly of weakly concave operators. Since the restriction of a hyponormal operator to its closed invariant subspace is again hyponormal, we conclude that
It turns out that all inclusions in (7.1) are proper if $\mathcal {H}$![]() is infinite dimensional (see Example 7.6). If $\mathcal {H}$
is infinite dimensional (see Example 7.6). If $\mathcal {H}$![]() is finite dimensional, then for every $k\in \mathbb {Z}_+ \cup \{\infty \}$
is finite dimensional, then for every $k\in \mathbb {Z}_+ \cup \{\infty \}$![]() , $\mathcal {A}_k$
, $\mathcal {A}_k$![]() consists exactly of unitary operators [see Proposition 3.2(i)].
consists exactly of unitary operators [see Proposition 3.2(i)].
An examination of the proof of Theorem 1.3 (using Proposition 3.2(i) in place of Corollary 3.3(i)) shows that it is true for operators of class $\mathcal {A}_{k}$![]() , where $k\in \mathbb {Z}_+ \cup \{\infty \}$
, where $k\in \mathbb {Z}_+ \cup \{\infty \}$![]() .
.
Theorem 7.2 Suppose that $T \in \mathcal {B}(\mathcal {H})$![]() is of class $\mathcal {A}_{\infty }$
is of class $\mathcal {A}_{\infty }$![]() . Let $\mathcal {H}_u$
. Let $\mathcal {H}_u$![]() and $\mathcal {H}'_u$
and $\mathcal {H}'_u$![]() denote the closed vector subspaces of $\mathcal {H}$
denote the closed vector subspaces of $\mathcal {H}$![]() given by (1.4). Then $\mathcal {H}'_u \subseteq \mathcal {H}_u$
given by (1.4). Then $\mathcal {H}'_u \subseteq \mathcal {H}_u$![]() and $\mathcal {H}'_u$
and $\mathcal {H}'_u$![]() reduces $T.$
reduces $T.$![]() Moreover,
Moreover,
where $U \in \mathcal {B}(\mathcal {H}'_u)$![]() is unitary and $S \in \mathcal {B}((\mathcal {H}'_u)^{\perp })$
is unitary and $S \in \mathcal {B}((\mathcal {H}'_u)^{\perp })$![]() has the wandering subspace property.
has the wandering subspace property.
Remark 7.3 Regarding Theorems 1.3 and 7.2, we make the following observation. Let $T \in {\mathcal {B}}(\mathcal {H})$![]() be an analytic expansion with $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$
be an analytic expansion with $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$![]() and let $T'$
and let $T'$![]() be the Cauchy dual of $T.$
be the Cauchy dual of $T.$![]() Set $R:=T'|_{\mathcal {H}'_u}$
Set $R:=T'|_{\mathcal {H}'_u}$![]() . Since the analyticity of $T$
. Since the analyticity of $T$![]() implies that $0\in \sigma (T)$
implies that $0\in \sigma (T)$![]() , it can be concluded from the proof of Theorem 1.3 that $R$
, it can be concluded from the proof of Theorem 1.3 that $R$![]() is an invertible contraction such that $\sigma _{ap}(R) \subseteq \partial \mathbb {D}$
is an invertible contraction such that $\sigma _{ap}(R) \subseteq \partial \mathbb {D}$![]() (see (6.1)), which together with the inclusion $\partial \sigma (R) \subseteq \sigma _{ap}(R)$
(see (6.1)), which together with the inclusion $\partial \sigma (R) \subseteq \sigma _{ap}(R)$![]() implies that $\sigma (R) \subseteq \partial \mathbb {D}$
implies that $\sigma (R) \subseteq \partial \mathbb {D}$![]() (the reader is referred to [Reference Stampfli41, Theorem 7], where a non-unitary contraction with spectrum being a nowhere dense perfect set of measure zero on the unit circle has been constructed). Thus $R$
(the reader is referred to [Reference Stampfli41, Theorem 7], where a non-unitary contraction with spectrum being a nowhere dense perfect set of measure zero on the unit circle has been constructed). Thus $R$![]() is unitary if and only if $R$
is unitary if and only if $R$![]() is hyponormal. In particular, this is the case if the restriction of $T'$
is hyponormal. In particular, this is the case if the restriction of $T'$![]() to the range of some power of it is hyponormal [see (7.1) and Theorem 7.2]. $\diamondsuit$
to the range of some power of it is hyponormal [see (7.1) and Theorem 7.2]. $\diamondsuit$![]()
In turn, Theorem 1.4 remains valid for operators of class $\mathcal {A}_{k}$![]() , where $k\in \mathbb {Z}_+$
, where $k\in \mathbb {Z}_+$![]() .
.
Theorem 7.4 Let $T \in \mathcal {B}(\mathcal {H})$![]() be an analytic finitely cyclic operator of class $\mathcal {A}_{k}$
be an analytic finitely cyclic operator of class $\mathcal {A}_{k}$![]() for some $k\in \mathbb {Z}_+.$
for some $k\in \mathbb {Z}_+.$![]() Then $T$
Then $T$![]() and $T'$
and $T'$![]() have trace class self-commutators. Moreover, for any complex polynomials $p, q$
have trace class self-commutators. Moreover, for any complex polynomials $p, q$![]() in two complex variables $z$
in two complex variables $z$![]() and $\bar z$
and $\bar z$![]() ,
,

where $dA$![]() denotes the Lebesgue planar measure.
denotes the Lebesgue planar measure.
Proof. According to Proposition 3.1, the case $k=1$![]() is precisely Theorem 1.4 (by (7.1), this implies the case $k=0$
is precisely Theorem 1.4 (by (7.1), this implies the case $k=0$![]() ). Assume now that $k \geqslant 2.$
). Assume now that $k \geqslant 2.$![]() Since $T$
Since $T$![]() is finitely cyclic, we infer from (6.2) that $\dim \ker T^* < \infty$
is finitely cyclic, we infer from (6.2) that $\dim \ker T^* < \infty$![]() . By the analyticity of $T$
. By the analyticity of $T$![]() , $\mathcal {H}_u=\{0\}$
, $\mathcal {H}_u=\{0\}$![]() , so by [Reference Shimorin35, Proposition 2.7(ii)] $T'$
, so by [Reference Shimorin35, Proposition 2.7(ii)] $T'$![]() is finitely cyclic with the cyclic space $\ker T^*$
is finitely cyclic with the cyclic space $\ker T^*$![]() . Since the range of $T^{\prime k}$
. Since the range of $T^{\prime k}$![]() is closed, we deduce that $R_k:=T'|_{{\mathcal {R}}(T^{\prime k})}$
is closed, we deduce that $R_k:=T'|_{{\mathcal {R}}(T^{\prime k})}$![]() is finitely cyclic with the cyclic space $T^{\prime k}(\ker T^*)$
is finitely cyclic with the cyclic space $T^{\prime k}(\ker T^*)$![]() (cf. (6.5)). By (${\rm iii}_{k}$
(cf. (6.5)). By (${\rm iii}_{k}$![]() ), $R_k$
), $R_k$![]() is hyponormal, so by [Reference Conway18, Theorem IV.2.1], $[R_k^*,R_k]$
is hyponormal, so by [Reference Conway18, Theorem IV.2.1], $[R_k^*,R_k]$![]() is of trace class. It follows from [Reference Shimorin35, Lemma 2.1] that
is of trace class. It follows from [Reference Shimorin35, Lemma 2.1] that

which yields $\dim {\mathcal {R}}(T^{\prime k})^{\perp } <\infty$![]() . This implies that $T'$
. This implies that $T'$![]() is a finite rank perturbation of the operator $R_k \oplus 0$
is a finite rank perturbation of the operator $R_k \oplus 0$![]() which has a trace class self-commutator. Thus, the self-commutator of $T'$
which has a trace class self-commutator. Thus, the self-commutator of $T'$![]() and consequently that of $T$
and consequently that of $T$![]() are of trace class (see (6.6)). It is also easy to see that (6.7) holds (with the same proof). Next, arguing as in last paragraph of the proof of Theorem 1.4 [with Proposition 3.2(ii) in place of Corollary 3.3(ii)], we conclude that (6.9) holds. Finally, applying the Carey–Pincus trace formula completes the proof.
are of trace class (see (6.6)). It is also easy to see that (6.7) holds (with the same proof). Next, arguing as in last paragraph of the proof of Theorem 1.4 [with Proposition 3.2(ii) in place of Corollary 3.3(ii)], we conclude that (6.9) holds. Finally, applying the Carey–Pincus trace formula completes the proof.
The next result generalizes [Reference Chavan12, Corollary 2.29], which was stated for concave operators, to operators of class $\mathcal {A}_k$![]() with $k\in \mathbb {Z}_+$
with $k\in \mathbb {Z}_+$![]() (see (7.1)). This is also related to [Reference Coburn16].
(see (7.1)). This is also related to [Reference Coburn16].
Corollary 7.5 Suppose that $\mathcal {H}\neq \{0\}$![]() and $T \in \mathcal {B}(\mathcal {H})$
and $T \in \mathcal {B}(\mathcal {H})$![]() is an analytic finitely cyclic operator of class $\mathcal {A}_{k},$
is an analytic finitely cyclic operator of class $\mathcal {A}_{k},$![]() where $k\in \mathbb {Z}_+.$
where $k\in \mathbb {Z}_+.$![]() Then $n: =\dim \ker T^*$
Then $n: =\dim \ker T^*$![]() is a positive integer and $T$
is a positive integer and $T$![]() is unitarily equivalent to a compact perturbation of $U^n_+$
is unitarily equivalent to a compact perturbation of $U^n_+$![]() , where $U_+$
, where $U_+$![]() is the unilateral shift of multiplicity $1.$
is the unilateral shift of multiplicity $1.$![]()
Proof. By Corollary 6.4, $n$![]() is a positive integer. Next, note that $U_+^n$
is a positive integer. Next, note that $U_+^n$![]() is a concave operator which is analytic and finitely cyclic with $\dim \ker (U_+^{n})^{*}=n$
is a concave operator which is analytic and finitely cyclic with $\dim \ker (U_+^{n})^{*}=n$![]() . Applying Corollary 6.4 to the operators $T$
. Applying Corollary 6.4 to the operators $T$![]() and $U_+^n$
and $U_+^n$![]() , we conclude that
, we conclude that
By Theorem 7.4, the operators $T$![]() and $U_+^n$
and $U_+^n$![]() have compact self-commutators. This together with (7.2), (7.3) and [Reference Douglas19, Theorem 2] completes the proof.
have compact self-commutators. This together with (7.2), (7.3) and [Reference Douglas19, Theorem 2] completes the proof.
The example below shows that if $\mathcal {H}$![]() is infinite dimensional, then all the inclusions in (7.1) are proper, i.e.,
is infinite dimensional, then all the inclusions in (7.1) are proper, i.e.,
and Theorem 7.4 is not true for operators of class $\mathcal {A}_{\infty }$![]() .
.
Example 7.6 [Example 5.4 continued]
As in Example 5.4, we assume that the unilateral weighted shift $W$![]() is left-invertible. Clearly, $W$
is left-invertible. Clearly, $W$![]() is cyclic with the cyclic vector $e_0$
is cyclic with the cyclic vector $e_0$![]() and is expansive if and only if
and is expansive if and only if
Fix $k\in \mathbb {Z}_+$![]() . Since $W$
. Since $W$![]() and $W'$
and $W'$![]() are unilateral weighted shifts, we have
are unilateral weighted shifts, we have

This implies that $W$![]() and $W'$
and $W'$![]() are analytic. By (7.6), the operator $W'|_{{\mathcal {R}}(W^{\prime k})}$
are analytic. By (7.6), the operator $W'|_{{\mathcal {R}}(W^{\prime k})}$![]() is unitarily equivalent to the unilateral weighted shift with weights $\{w_{k+n}^{-1}\}_{n=0}^{\infty }$
is unitarily equivalent to the unilateral weighted shift with weights $\{w_{k+n}^{-1}\}_{n=0}^{\infty }$![]() . Hence, by [Reference Conway18, Proposition II.6.6], $W'|_{{\mathcal {R}}(W^{\prime k})}$
. Hence, by [Reference Conway18, Proposition II.6.6], $W'|_{{\mathcal {R}}(W^{\prime k})}$![]() is hyponormal if and only if
is hyponormal if and only if
Consider now the inequality
and note that the following implication is valid.
Indeed, if $\varepsilon > 0$![]() , then $\sup _{n\geqslant l} w_n \leqslant 1+\varepsilon$
, then $\sup _{n\geqslant l} w_n \leqslant 1+\varepsilon$![]() for some integer $l\geqslant 1$
for some integer $l\geqslant 1$![]() , so
, so
with $M:= \max \left \{1, w_{l-1}, w_{l-1}\cdot w_{l-2}, \ldots, w_{l-1} \cdots w_{0}\right \}.$![]() By Gelfand's formula,
By Gelfand's formula,
which yields $r(W)\leqslant 1$![]() .
.
Combining (7.9) and Remark 1.2 with the analyticity of $W'$![]() , we obtain the following sufficient condition for membership in the classFootnote 2 $\mathcal {A}_{\infty }$
, we obtain the following sufficient condition for membership in the classFootnote 2 $\mathcal {A}_{\infty }$![]() .
.
Moreover, the following necessary and sufficient condition for membership in the class $\mathcal {A}_k$![]() with $k \in \mathbb {Z}_+$
with $k \in \mathbb {Z}_+$![]() can be deduced from [Reference Shields37, Proposition 15] and Remark 1.2.
can be deduced from [Reference Shields37, Proposition 15] and Remark 1.2.
It is now easy to deduce from (7.10) and (7.11) that
To obtain the operator of class $\mathcal {A}_0$![]() that is not concave, we proceed as follows. By [Reference Jabłoński, Jung and Stochel25, Proposition A.2], the unilateral weighted shift $W$
that is not concave, we proceed as follows. By [Reference Jabłoński, Jung and Stochel25, Proposition A.2], the unilateral weighted shift $W$![]() with weight sequence $\left \{\frac {n+2}{n+1}\right \}_{n=0}^{\infty }$
with weight sequence $\left \{\frac {n+2}{n+1}\right \}_{n=0}^{\infty }$![]() is a strict $3$
is a strict $3$![]() -isometric expansion. Since $W'$
-isometric expansion. Since $W'$![]() is the unilateral weighted shift with weight sequence $\left \{\frac {n+1}{n+2}\right \}_{n=0}^{\infty }$
is the unilateral weighted shift with weight sequence $\left \{\frac {n+1}{n+2}\right \}_{n=0}^{\infty }$![]() which is increasing, $W'$
which is increasing, $W'$![]() is hyponormal, meaning that $W$
is hyponormal, meaning that $W$![]() is of class $\mathcal {A}_0$
is of class $\mathcal {A}_0$![]() . However, by Proposition 4.4, $W$
. However, by Proposition 4.4, $W$![]() is not concave. This justifies all the strict inclusions in (7.4).
is not concave. This justifies all the strict inclusions in (7.4).
The modulus of the self-commutator $[W^*,W]$![]() of $W$
of $W$![]() is the diagonal operator (relative to $\{e_n\}_{n=0}^{\infty }$
is the diagonal operator (relative to $\{e_n\}_{n=0}^{\infty }$![]() ) with diagonal elements $\{|w_n^2 - w_{n-1}^2|\}_{n=0}^{\infty }$
) with diagonal elements $\{|w_n^2 - w_{n-1}^2|\}_{n=0}^{\infty }$![]() , where $w_{-1}:=0$
, where $w_{-1}:=0$![]() . Suppose that $k\in \mathbb {Z}_+$
. Suppose that $k\in \mathbb {Z}_+$![]() and $W$
and $W$![]() is of class $\mathcal {A}_k$
is of class $\mathcal {A}_k$![]() . Then, by (7.11), we have
. Then, by (7.11), we have

which means that $[W^*,W]$![]() is of trace class. The above reasoning can be used to compute the trace $\mathrm {tr}\, [W^*,W]$
is of trace class. The above reasoning can be used to compute the trace $\mathrm {tr}\, [W^*,W]$![]() of the self-commutator $[W^*,W]$
of the self-commutator $[W^*,W]$![]() :
:

Certainly, the fact that $W$![]() has a trace class self-commutator as well as the formula (7.12) are particular cases of what is in Theorem 7.4 with the polynomials $p(z,\bar z) = \bar z$
has a trace class self-commutator as well as the formula (7.12) are particular cases of what is in Theorem 7.4 with the polynomials $p(z,\bar z) = \bar z$![]() and $q(z,\bar z) = z$
and $q(z,\bar z) = z$![]() .
.
Consider now the case where $W$![]() satisfies (7.5) and (7.8). By (7.10), $W$
satisfies (7.5) and (7.8). By (7.10), $W$![]() is of class $\mathcal {A}_{\infty }$
is of class $\mathcal {A}_{\infty }$![]() . Clearly, $\lim _{n\to \infty } w_n=1$
. Clearly, $\lim _{n\to \infty } w_n=1$![]() . Then $[W^*,W]$
. Then $[W^*,W]$![]() , being the diagonal operator with diagonal elements $\{w_n^2 - w_{n-1}^2\}_{n=0}^{\infty }$
, being the diagonal operator with diagonal elements $\{w_n^2 - w_{n-1}^2\}_{n=0}^{\infty }$![]() converging to $0$
converging to $0$![]() , is compact.
, is compact.
Now we construct a unilateral weighted shift $W$![]() of class $\mathcal {A}_{\infty }$
of class $\mathcal {A}_{\infty }$![]() such that the self-commutator $[W^*,W]$
such that the self-commutator $[W^*,W]$![]() of $W$
of $W$![]() is not of trace class (recall that $W$
is not of trace class (recall that $W$![]() is analytic and cyclic). Let $\{w_n\}_{n=0}^{\infty }$
is analytic and cyclic). Let $\{w_n\}_{n=0}^{\infty }$![]() be defined by
be defined by
where $\alpha _l = \sqrt {1+\frac 1{2^l}}$![]() for $l=1,2,\ldots$
for $l=1,2,\ldots$![]() . Straightforward computations show that
. Straightforward computations show that

which means that $[W^*,W]$![]() is not of trace class. Since $W$
is not of trace class. Since $W$![]() satisfies (7.5) and (7.8), we infer from (7.10) that $W$
satisfies (7.5) and (7.8), we infer from (7.10) that $W$![]() is of class $\mathcal {A}_{\infty }$
is of class $\mathcal {A}_{\infty }$![]() . $\diamondsuit$
. $\diamondsuit$![]()
As shown in Example 7.6 (see its last paragraph), Theorem 7.4 ceases to be true for operators of class $\mathcal {A}_{\infty }$![]() . However, in this example $\mathcal {H}_{u}'=\{0\}$
. However, in this example $\mathcal {H}_{u}'=\{0\}$![]() and the operator in question has a compact self-commutator. This motivates us to ask the following question which is closely related to Corollaries 6.4 and 7.5.
and the operator in question has a compact self-commutator. This motivates us to ask the following question which is closely related to Corollaries 6.4 and 7.5.
Question 7.7 Is an analytic finitely cyclic operator $T$![]() of class $\mathcal {A}_{\infty }$
of class $\mathcal {A}_{\infty }$![]() unitarily equivalent to a compact perturbation of $U^n_+$
unitarily equivalent to a compact perturbation of $U^n_+$![]() , where $n=\dim \ker (T^*)$
, where $n=\dim \ker (T^*)$![]() ?
?
8. Characterizations of classes $\mathcal {A}_k$
In this section, we characterize the left-invertible operators $T$![]() satisfying the condition (${\rm iii}_{k}$
satisfying the condition (${\rm iii}_{k}$![]() ) of Definition 7.1, where $k\in \mathbb {Z}_+ \cup \{\infty \}$
) of Definition 7.1, where $k\in \mathbb {Z}_+ \cup \{\infty \}$![]() . In particular, we obtain characterizations of classes $\mathcal {A}_k.$
. In particular, we obtain characterizations of classes $\mathcal {A}_k.$![]() We begin with an observation of independent interest.
We begin with an observation of independent interest.
Lemma 8.1 Let $T \in \mathcal {B}(\mathcal {H})$![]() be left-invertible and let $k$
be left-invertible and let $k$![]() be a positive integer. Then the range of $T'^k$
be a positive integer. Then the range of $T'^k$![]() is given by
is given by

Proof. Using [Reference Shimorin35, Lemma 2.1], the fact that the range of $T^{\prime k}$![]() is closed and finally Proposition 2.1(iii), we get
is closed and finally Proposition 2.1(iii), we get

This completes the proof.
The hyponormality of $T'|_{{\mathcal {R}}(T^{\prime k})}$![]() can now be characterized as follows.
can now be characterized as follows.
Proposition 8.2 Let $T \in \mathcal {B}(\mathcal {H})$![]() be left-invertible and $k\in \mathbb {Z}_+$
be left-invertible and $k\in \mathbb {Z}_+$![]() . Set $C_k = T^{\prime *k} T^{\prime k}$
. Set $C_k = T^{\prime *k} T^{\prime k}$![]() . Then $C_k$
. Then $C_k$![]() is invertible and the following conditions are equivalent:
is invertible and the following conditions are equivalent:
(i) $T'|_{{\mathcal {R}}(T^{\prime k})}$
 is hyponormal,
is hyponormal,(ii) $C_k^{1/2} T' C_k^{-1/2}$
 is hyponormal.
is hyponormal.
Proof. Since $T^{\prime k}$![]() is left-invertible, $C_k$
is left-invertible, $C_k$![]() is invertible and, by Proposition 2.1(iii), we have
is invertible and, by Proposition 2.1(iii), we have
It is easily seen that $T'|_{{\mathcal {R}}(T^{\prime k})}$![]() is hyponormal if and only if
is hyponormal if and only if
or equivalently, by (8.1), if and only if
which in turn is equivalent to
As a consequence, $T'|_{{\mathcal {R}}(T^{\prime k})}$![]() is hyponormal if and only if
is hyponormal if and only if
which completes the proof.
Corollary 8.3 Suppose that $T\in \mathcal {B}(\mathcal {H})$![]() is left-invertible and $T=U|T|$
is left-invertible and $T=U|T|$![]() is the polar decomposition of $T.$
is the polar decomposition of $T.$![]() Then $T'|_{{\mathcal {R}}(T')}$
Then $T'|_{{\mathcal {R}}(T')}$![]() is hyponormal if and only if $|T|^{-1} U$
is hyponormal if and only if $|T|^{-1} U$![]() is hyponormal. In particular, if $T'$
is hyponormal. In particular, if $T'$![]() is hyponormal, then $|T|^{-1} U$
is hyponormal, then $|T|^{-1} U$![]() is hyponormal.
is hyponormal.
Proof. It follows from Proposition 2.1(i) that
Combined with Proposition 8.2, this completes the proof.
Corollary 8.4 If $T\in \mathcal {B}(\mathcal {H})$![]() is of class $\mathcal {A}_k$
is of class $\mathcal {A}_k$![]() for some $k\in \mathbb {Z}_+$
for some $k\in \mathbb {Z}_+$![]() , then $T'$
, then $T'$![]() is similar to a hyponormal operator.
is similar to a hyponormal operator.
Corollary 8.5 Let $T \in \mathcal {B}(\mathcal {H})$![]() be an operator of class $\mathcal {A}_k$
be an operator of class $\mathcal {A}_k$![]() for some $k\in \mathbb {Z}_+.$
for some $k\in \mathbb {Z}_+.$![]() Then the operator $S_k:=C^{1/2}_k T' C^{-1/2}_k$
Then the operator $S_k:=C^{1/2}_k T' C^{-1/2}_k$![]() is a $2$
is a $2$![]() -hypercontraction, that is
-hypercontraction, that is

In particular,
Proof. By Proposition 7.2, the operator $S_k$![]() is hyponormal. It follows that
is hyponormal. It follows that
which gives (8.2) for $m=2$![]() (this is true for all hyponormal operators). It is now easy to see that (8.2) for $m=2$
(this is true for all hyponormal operators). It is now easy to see that (8.2) for $m=2$![]() is equivalent to
is equivalent to
which in turn is equivalent to (8.3).
Since $T^*T \geqslant I,$![]() we deduce that
we deduce that
Consequently, we have
or equivalently that
This gives
which shows that (8.2) holds for $m=1.$![]() This completes the proof.
This completes the proof.
Remark 8.6 Regarding the operator $C_k^{1/2} T' C_k^{-1/2}$![]() that appears in Proposition 8.2, observe that if $A\in \mathcal {B}(\mathcal {H})$
that appears in Proposition 8.2, observe that if $A\in \mathcal {B}(\mathcal {H})$![]() is positive and invertible and $T\in \mathcal {B}(\mathcal {H})$
is positive and invertible and $T\in \mathcal {B}(\mathcal {H})$![]() , then the adjoint of $T$
, then the adjoint of $T$![]() with respect to the (equivalent) inner product $\langle {A(\cdot )},\,{-} \rangle$
with respect to the (equivalent) inner product $\langle {A(\cdot )},\,{-} \rangle$![]() , is equal to $(ATA^{-1})^*$
, is equal to $(ATA^{-1})^*$![]() . In turn, if $T\in \mathcal {B}(\mathcal {H})$
. In turn, if $T\in \mathcal {B}(\mathcal {H})$![]() is left-invertible and $T=U|T|$
is left-invertible and $T=U|T|$![]() is the polar decomposition of $T$
is the polar decomposition of $T$![]() , then by Proposition 2.1, $T'= U|T|^{-1}$
, then by Proposition 2.1, $T'= U|T|^{-1}$![]() is the polar decomposition of $T',$
is the polar decomposition of $T',$![]() so the operator $|T|^{-1} U$
so the operator $|T|^{-1} U$![]() that appears in Corollary 8.3 is the Duggal transformFootnote 3 of $T'.$
that appears in Corollary 8.3 is the Duggal transformFootnote 3 of $T'.$![]() Finally, the concept of $m$
Finally, the concept of $m$![]() -hypercontractivity that appears in Corollary 8.5 was introduced by Agler in [Reference Agler2]. $\diamondsuit$
-hypercontractivity that appears in Corollary 8.5 was introduced by Agler in [Reference Agler2]. $\diamondsuit$![]()
The following characterization of the hyponormality of $T'|_{\mathcal {H}_{u}'}$![]() can be viewed as an asymptotic version of Proposition 8.2 (see Remark 8.8).
can be viewed as an asymptotic version of Proposition 8.2 (see Remark 8.8).
Proposition 8.7 Let $T \in \mathcal {B}(\mathcal {H})$![]() be left-invertible and let $C_k = T^{\prime *k} T^{\prime k}$
be left-invertible and let $C_k = T^{\prime *k} T^{\prime k}$![]() for $k\in \mathbb {Z}_+$
for $k\in \mathbb {Z}_+$![]() . Then $\{T^{\prime (k+1)} C_k^{-1} T^{\prime * (k+1)}\}_{k=0}^{\infty }$
. Then $\{T^{\prime (k+1)} C_k^{-1} T^{\prime * (k+1)}\}_{k=0}^{\infty }$![]() and $\{T^{\prime k}C_k^{-1} C_{k+1} C_k^{-1} T^{\prime * k}\}_{k=0}^{\infty }$
and $\{T^{\prime k}C_k^{-1} C_{k+1} C_k^{-1} T^{\prime * k}\}_{k=0}^{\infty }$![]() converge in SOT $($
converge in SOT $($![]() the strong operator topology$)$
the strong operator topology$)$![]() to positive operators denoted by $A$
to positive operators denoted by $A$![]() and $B$
and $B$![]() , respectively, and the following conditions are equivalent:
, respectively, and the following conditions are equivalent:
(i) $T'|_{\mathcal {H}_{u}'}$
 is hyponormal,
is hyponormal,(ii) $A \leqslant B$
 ,
,(iii) for all $h\in \mathcal {H}$
 ,
\[ \lim_{k\to \infty} \|(C_k^{1/2}T'C_k^{{-}1/2})^* C_k^{{-}1/2} T^{\prime * k}h\|^2 \leqslant \lim_{k\to\infty} \|C_k^{1/2}T'C_k^{{-}1/2} C_k^{{-}1/2} T^{\prime * k}h\|^2, \]
,
\[ \lim_{k\to \infty} \|(C_k^{1/2}T'C_k^{{-}1/2})^* C_k^{{-}1/2} T^{\prime * k}h\|^2 \leqslant \lim_{k\to\infty} \|C_k^{1/2}T'C_k^{{-}1/2} C_k^{{-}1/2} T^{\prime * k}h\|^2, \]
(iv) $P_{\mathcal {H}_{u}'} ((T^*T)^{-1} - T^{\prime } P_{\mathcal {H}_{u}'} T^{\prime *}) P_{\mathcal {H}_{u}'} \geqslant 0$
 .
.
Moreover, $A=P_{\mathcal {H}_{u}'} T^{\prime } P_{\mathcal {H}_{u}'} T^{\prime *} P_{\mathcal {H}_{u}'}$![]() and $B=P_{\mathcal {H}_{u}'} (T^*T)^{-1} P_{\mathcal {H}_{u}'}.$
and $B=P_{\mathcal {H}_{u}'} (T^*T)^{-1} P_{\mathcal {H}_{u}'}.$![]()
Proof. Set $P_k=P_{{\mathcal {R}}(T^{\prime k})}$![]() for $k \in \mathbb {Z}_+$
for $k \in \mathbb {Z}_+$![]() and $P_{\infty } = P_{\mathcal {H}_{u}'}$
and $P_{\infty } = P_{\mathcal {H}_{u}'}$![]() . Since ${\mathcal {R}}(T^{\prime k}) \searrow \mathcal {H}_{u}'$
. Since ${\mathcal {R}}(T^{\prime k}) \searrow \mathcal {H}_{u}'$![]() as $k\nearrow \infty$
as $k\nearrow \infty$![]() , we deduce that $P_k \searrow P_{\infty }$
, we deduce that $P_k \searrow P_{\infty }$![]() as $k\nearrow \infty$
as $k\nearrow \infty$![]() in SOT. By the sequential SOT-continuity of multiplication in $\mathcal {B}(\mathcal {H})$
in SOT. By the sequential SOT-continuity of multiplication in $\mathcal {B}(\mathcal {H})$![]() , we deduce that
, we deduce that
Observe now that,
which yields

Combined with (8.4), this implies that the sequence $\{T^{\prime (k+1)}C_k^{-1} T^{\prime *(k+1)}\}_{n=0}^{\infty }$![]() converges in SOT to $A=P_{\infty } T^{\prime } P_{\infty } T^{\prime *} P_{\infty }$
converges in SOT to $A=P_{\infty } T^{\prime } P_{\infty } T^{\prime *} P_{\infty }$![]() , and
, and
A similar argument shows that
so by (8.5) the sequence $\{T^{\prime k}C_k^{-1} C_{k+1} C_k^{-1} T^{\prime * k}\}_{n=0}^{\infty }$![]() converges in SOT to $B=P_{\infty } (T^*T)^{-1} P_{\infty }$
converges in SOT to $B=P_{\infty } (T^*T)^{-1} P_{\infty }$![]() , and moreover:
, and moreover:
(i)$\Leftrightarrow$![]() (ii) It is easy to see that $T'|_{\mathcal {H}_{u}'}$
(ii) It is easy to see that $T'|_{\mathcal {H}_{u}'}$![]() is hyponormal if and only if
is hyponormal if and only if
or equivalently, by (8.4) and (8.5), if and only if
Combined with (8.6) and (8.8), this shows that (i) and (ii) are equivalent.
(ii)$\Leftrightarrow$![]() (iii) This follows from (8.7) and (8.9).
(iii) This follows from (8.7) and (8.9).
(ii)$\Leftrightarrow$![]() (iv) This is a consequence of the identities $A=P_{\infty } T^{\prime } P_{\infty } T^{\prime *} P_{\infty }$
(iv) This is a consequence of the identities $A=P_{\infty } T^{\prime } P_{\infty } T^{\prime *} P_{\infty }$![]() and $B=P_{\infty } (T^*T)^{-1} P_{\infty }$
and $B=P_{\infty } (T^*T)^{-1} P_{\infty }$![]() .
.
Remark 8.8 Regarding Proposition 8.7(iii), note that in view of Proposition 2.1(i) applied to $T^{\prime k}$![]() , the operator $T^{\prime k}C_k^{-1/2}$
, the operator $T^{\prime k}C_k^{-1/2}$![]() is an isometry. This implies that the range of $C_k^{-1/2} T^{\prime * k}$
is an isometry. This implies that the range of $C_k^{-1/2} T^{\prime * k}$![]() is equal to $\mathcal {H}$
is equal to $\mathcal {H}$![]() . As a consequence, for a fixed $k\in \mathbb {Z}_+$
. As a consequence, for a fixed $k\in \mathbb {Z}_+$![]() , the inequality
, the inequality
is equivalent to
which according to Proposition 8.2 is equivalent to the hyponormality of $T'|_{{\mathcal {R}}(T^{\prime k})}$![]() . From this point of view, Proposition 8.7 can be seen as an asymptotic version of Proposition 8.2. $\diamondsuit$
. From this point of view, Proposition 8.7 can be seen as an asymptotic version of Proposition 8.2. $\diamondsuit$![]()
9. $C^*$ - and $W^*$
- and $W^*$ -algebra analogues of $\mathcal {A}_k$
-algebra analogues of $\mathcal {A}_k$
We conclude the paper by discussing the possibility of defining membership in the classes $\mathcal {A}_k$![]() , $k\in \mathbb {Z}_+ \cup \{\infty \}$
, $k\in \mathbb {Z}_+ \cup \{\infty \}$![]() , for elements of an abstract unital $C^*$
, for elements of an abstract unital $C^*$![]() -algebra. This question is in the spirit of [Reference Bunce9, Reference Bunce and Deddens10, Reference Szafraniec42].
-algebra. This question is in the spirit of [Reference Bunce9, Reference Bunce and Deddens10, Reference Szafraniec42].
Let $\mathcal {C}$![]() be a $C^*$
be a $C^*$![]() -algebra with unit $e.$
-algebra with unit $e.$![]() Set $\mathcal {C}_r := \{t\in \mathcal {C}\colon \|t\|\leqslant r\}$
Set $\mathcal {C}_r := \{t\in \mathcal {C}\colon \|t\|\leqslant r\}$![]() for $r\in (0,\infty ).$
for $r\in (0,\infty ).$![]() Fix $t\in \mathcal {C}$
Fix $t\in \mathcal {C}$![]() . Denote by $C^*(t)$
. Denote by $C^*(t)$![]() the $C^*$
the $C^*$![]() -algebra generated by $t$
-algebra generated by $t$![]() and $e.$
and $e.$![]() We say that $t$
We say that $t$![]() is hyponormal if $t^*t - tt^*$
is hyponormal if $t^*t - tt^*$![]() is a positive element of $\mathcal {C}$
is a positive element of $\mathcal {C}$![]() . If $t^*t$
. If $t^*t$![]() is invertible, then the element $t':= t (t^*t)^{-1}$
is invertible, then the element $t':= t (t^*t)^{-1}$![]() is called the Cauchy dual of $t$
is called the Cauchy dual of $t$![]() . Clearly, if $t^*t$
. Clearly, if $t^*t$![]() is invertible, then $t$
is invertible, then $t$![]() is left-invertible (with the left-inverse $t^{\prime *}$
is left-invertible (with the left-inverse $t^{\prime *}$![]() ). The converse implication is true, as can be seen by using the Gelfand–Naimark representation theorem (see [Reference Rudin33, Theorem 12.41]) and [Reference Conway17, Proposition VIII.1.14]. Namely, the following equivalences are valid:
). The converse implication is true, as can be seen by using the Gelfand–Naimark representation theorem (see [Reference Rudin33, Theorem 12.41]) and [Reference Conway17, Proposition VIII.1.14]. Namely, the following equivalences are valid:
In particular, if $t$![]() is an expansion, that is $t^*t \geqslant e$
is an expansion, that is $t^*t \geqslant e$![]() , then $t$
, then $t$![]() is left-invertible. Moreover, if $t$
is left-invertible. Moreover, if $t$![]() is left-invertible, then so is $t'$
is left-invertible, then so is $t'$![]() and consequently $t^{\prime k}$
and consequently $t^{\prime k}$![]() for every $k\in \mathbb {Z}_+$
for every $k\in \mathbb {Z}_+$![]() . As a consequence of (9.1), $c_k := t^{\prime *k} t^{\prime k}$
. As a consequence of (9.1), $c_k := t^{\prime *k} t^{\prime k}$![]() is invertible. Observe also that if $t\in \mathcal {C}$
is invertible. Observe also that if $t\in \mathcal {C}$![]() is left-invertible, then $t=(t^{\prime })^{\prime }$
is left-invertible, then $t=(t^{\prime })^{\prime }$![]() so by (9.1) and [Reference Conway17, Proposition VIII.1.14], the $C^*$
so by (9.1) and [Reference Conway17, Proposition VIII.1.14], the $C^*$![]() -algebras $C^*(t)$
-algebras $C^*(t)$![]() and $C^*(t^{\prime })$
and $C^*(t^{\prime })$![]() coincide. We now give the $C^*$
coincide. We now give the $C^*$![]() -algebra analogue of the class $\mathcal {A}_k$
-algebra analogue of the class $\mathcal {A}_k$![]() for $k\in \mathbb {Z}_+.$
for $k\in \mathbb {Z}_+.$![]()
Definition 9.1 Let $\mathcal {C}$![]() be a unital $C^*$
be a unital $C^*$![]() -algebra and let $k\in \mathbb {Z}_+.$
-algebra and let $k\in \mathbb {Z}_+.$![]() We say that $t\in \mathcal {C}$
We say that $t\in \mathcal {C}$![]() is of class $\mathcal {A}_k$
is of class $\mathcal {A}_k$![]() if
if
• the spectral radius of $t$
 is at most $1$
is at most $1$ ,
,• $t$
 is an expansion,
is an expansion,• $c_k^{1/2} t' c_k^{-1/2}$
 is hyponormal.
is hyponormal.
Using Remark 1.2 and Proposition 8.2, we see that Definitions 7.1 and 9.1 coincide for $k\in \mathbb {Z}_+$![]() if $\mathcal {C} = \mathcal {B}(\mathcal {H})$
if $\mathcal {C} = \mathcal {B}(\mathcal {H})$![]() .
.
Remark 9.2 First observe that if $\mathcal {C}$![]() is a $C^*$
is a $C^*$![]() -algebra with unit $e$
-algebra with unit $e$![]() and $t\in \mathcal {C}$
and $t\in \mathcal {C}$![]() is of class $\mathcal {A}_k$
is of class $\mathcal {A}_k$![]() for some $k\in \mathbb {Z}_+,$
for some $k\in \mathbb {Z}_+,$![]() then $C^*(t)$
then $C^*(t)$![]() is commutative if and only if $t$
is commutative if and only if $t$![]() is unitary, that is, $t^*t=tt^*=e.$
is unitary, that is, $t^*t=tt^*=e.$![]()
Note that if $t$![]() is a left-invertible element of a unital $C^*$
is a left-invertible element of a unital $C^*$![]() -algebra $\mathcal {C}$
-algebra $\mathcal {C}$![]() , then $t^{\prime }=t$
, then $t^{\prime }=t$![]() if and only if $t$
if and only if $t$![]() is an isometric element of $\mathcal {C}$
is an isometric element of $\mathcal {C}$![]() (use the fact that $t^{\prime *}$
(use the fact that $t^{\prime *}$![]() is a left-inverse of $t$
is a left-inverse of $t$![]() ). It is worth mentioning that the $C^*$
). It is worth mentioning that the $C^*$![]() -algebra generated by a single isometry was studied in [Reference Coburn16].
-algebra generated by a single isometry was studied in [Reference Coburn16].
If $\mathcal {C}_1$![]() and $\mathcal {C}_2$
and $\mathcal {C}_2$![]() are two unital $C^*$
are two unital $C^*$![]() -algebras, $\pi \colon \mathcal {C}_1 \to \mathcal {C}_2$
-algebras, $\pi \colon \mathcal {C}_1 \to \mathcal {C}_2$![]() is a $*$
is a $*$![]() -isomorphism and $t_1\in \mathcal {C}_1$
-isomorphism and $t_1\in \mathcal {C}_1$![]() and $t_2\in \mathcal {C}_2$
and $t_2\in \mathcal {C}_2$![]() are such that $\pi (t_1) = t_2,$
are such that $\pi (t_1) = t_2,$![]() then for each $k\in \mathbb {Z}_+$
then for each $k\in \mathbb {Z}_+$![]() , $t_1$
, $t_1$![]() is of class $\mathcal {A}_k$
is of class $\mathcal {A}_k$![]() if and only if $t_2$
if and only if $t_2$![]() is of class $\mathcal {A}_k.$
is of class $\mathcal {A}_k.$![]() $\diamondsuit$
$\diamondsuit$![]()
The case of the class $\mathcal {A}_{\infty }$![]() is more delicate. As we will show below, the membership in this class can be satisfactorily defined in the context of $W^*$
is more delicate. As we will show below, the membership in this class can be satisfactorily defined in the context of $W^*$![]() -algebras, which are more special objects compared to $C^*$
-algebras, which are more special objects compared to $C^*$![]() -algebras (see Definitions 9.6 and 9.7). Several properties of certain sequences associated with an expansion are needed for this.
-algebras (see Definitions 9.6 and 9.7). Several properties of certain sequences associated with an expansion are needed for this.
Proposition 9.3 Let $\mathcal {C}$![]() be a $C^*$
be a $C^*$![]() -algebra with unit $e$
-algebra with unit $e$![]() and $t\in \mathcal {C}$
and $t\in \mathcal {C}$![]() be an expansion. Define the sequences $\{p_k\}_{k=0}^{\infty },$
be an expansion. Define the sequences $\{p_k\}_{k=0}^{\infty },$![]() $\{u_k\}_{k=0}^{\infty }$
$\{u_k\}_{k=0}^{\infty }$![]() and $\{v_k\}_{k=0}^{\infty }$
and $\{v_k\}_{k=0}^{\infty }$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() by
by
Then the following statements hold for all $k\in \mathbb {Z}_+$![]() :
:
(i) $p_k=p_k^*p_k,$
 $p_kp_{k+1}=p_{k+1}$
$p_kp_{k+1}=p_{k+1}$ and $0 \leqslant p_{k+1} \leqslant p_k \leqslant e,$
and $0 \leqslant p_{k+1} \leqslant p_k \leqslant e,$
(ii) $0 \leqslant c_{k+1} \leqslant c_k \leqslant e$
 and $c_k^{-1/2} c_{k+1} c_k^{-1/2} \leqslant e,$
and $c_k^{-1/2} c_{k+1} c_k^{-1/2} \leqslant e,$
(iii) $u_k=t^{\prime } p_k t^{\prime *},$
 $0 \leqslant t^{\prime (k+1)} t^{\prime * (k+1)} \leqslant u_k \leqslant p_{k+1} \leqslant e$
$0 \leqslant t^{\prime (k+1)} t^{\prime * (k+1)} \leqslant u_k \leqslant p_{k+1} \leqslant e$ and $u_{k+1} \leqslant u_k,$
and $u_{k+1} \leqslant u_k,$
(iv) $v_{k+1} = p_{k+1} v_k p_{k+1},$
 $v_k = p_k t^{\prime *}t^{\prime } p_k$
$v_k = p_k t^{\prime *}t^{\prime } p_k$ and $0 \leqslant v_k \leqslant p_k \leqslant e.$
and $0 \leqslant v_k \leqslant p_k \leqslant e.$
Moreover, $t$![]() is an expansive element of $C^*(t)$
is an expansive element of $C^*(t)$![]() and the elements $t^{\prime }$
and the elements $t^{\prime }$![]() , $c_k$
, $c_k$![]() , $c_k^{-1}$
, $c_k^{-1}$![]() , $p_k$
, $p_k$![]() , $u_k$
, $u_k$![]() and $v_k$
and $v_k$![]() belong to $C^*(t).$
belong to $C^*(t).$![]()
Proof. (i) By definition, $p_k=p_k^*$![]() and
and
so $p_k=p_k^*p_k$![]() for all $k\in \mathbb {Z}_+.$
for all $k\in \mathbb {Z}_+.$![]() Since
Since
and thus $p_kp_{k+1}=p_{k+1}p_k$![]() for all $k\in \mathbb {Z}_+,$
for all $k\in \mathbb {Z}_+,$![]() we deduce that
we deduce that
Hence, $p_{k+1} \leqslant p_k$![]() for all $k\in \mathbb {Z}_+$
for all $k\in \mathbb {Z}_+$![]() . Since $e-p_k$
. Since $e-p_k$![]() is a self-adjoint idempotent, we see that $p_k \leqslant e$
is a self-adjoint idempotent, we see that $p_k \leqslant e$![]() for all $k\in \mathbb {Z}_+.$
for all $k\in \mathbb {Z}_+.$![]() This proves (i).
This proves (i).
(ii) We can argue as in the second paragraph of the proof of Corollary 8.5 (the arguments given there are purely $C^*$![]() -algebraic).
-algebraic).
(iii) The identity $u_k=t^{\prime } p_k t^{\prime *}$![]() is obvious. It follows from (ii) that $c_k^{-1} \geqslant e$
is obvious. It follows from (ii) that $c_k^{-1} \geqslant e$![]() and $c_k^{-1} \leqslant c_{k+1}^{-1}$
and $c_k^{-1} \leqslant c_{k+1}^{-1}$![]() for all $k\in \mathbb {Z}_+$
for all $k\in \mathbb {Z}_+$![]() , so
, so

which gives the second part of (iii). The third part of (iii) follows from
(iv) It is easy to see that the identity $v_k = p_k t^{\prime *}t^{\prime } p_k$![]() is valid. Hence, by (i) and (ii), we have
is valid. Hence, by (i) and (ii), we have
which proves the third part of (iv). Finally, we come to the conclusion that
which gives the first identity in (iv).
The proof of the ‘moreover’ part is as follows. That $t$![]() is an expansive element of $C^*(t)$
is an expansive element of $C^*(t)$![]() and $t^{\prime }, c_k, c_k^{-1} \in C^*(t)$
and $t^{\prime }, c_k, c_k^{-1} \in C^*(t)$![]() for every $k\in \mathbb {Z}_+$
for every $k\in \mathbb {Z}_+$![]() follows from (9.1) and the fact that $\sigma _{C^*(t)}(s)=\sigma _{\mathcal {C}}(s)$
follows from (9.1) and the fact that $\sigma _{C^*(t)}(s)=\sigma _{\mathcal {C}}(s)$![]() for every $s \in C^*(t)$
for every $s \in C^*(t)$![]() (see [Reference Conway17, Proposition VIII.1.14]; see also [Reference Conway17, Theorem VIII.3.6]). As a consequence, each of the elements $p_k$
(see [Reference Conway17, Proposition VIII.1.14]; see also [Reference Conway17, Theorem VIII.3.6]). As a consequence, each of the elements $p_k$![]() , $u_k$
, $u_k$![]() and $v_k$
and $v_k$![]() belongs to $C^*(t).$
belongs to $C^*(t).$![]() This completes the proof.
This completes the proof.
The following property of elements of class $\mathcal {A}_k$![]() is a direct consequence of Proposition 9.3 and [Reference Conway17, Proposition VIII.1.14]. We will call it $C^*$
is a direct consequence of Proposition 9.3 and [Reference Conway17, Proposition VIII.1.14]. We will call it $C^*$![]() -permanence property which is shared by some other classes of elements of a unital $C^*$
-permanence property which is shared by some other classes of elements of a unital $C^*$![]() -algebra, including hyponormal ones.
-algebra, including hyponormal ones.
Corollary 9.4 If $\mathcal {C}$![]() is a unital $C^*$
is a unital $C^*$![]() -algebra, $t\in \mathcal {C}$
-algebra, $t\in \mathcal {C}$![]() and $k\in \mathbb {Z}_+,$
and $k\in \mathbb {Z}_+,$![]() then $t$
then $t$![]() is of class $\mathcal {A}_k$
is of class $\mathcal {A}_k$![]() if and only if $t$
if and only if $t$![]() is of class $\mathcal {A}_k$
is of class $\mathcal {A}_k$![]() as an element of $C^*(t).$
as an element of $C^*(t).$![]()
The question of the existence of limits of sequences that were defined in (9.2) is discussed below in the context of $W^*$![]() -algebras. Given an element $t$
-algebras. Given an element $t$![]() of a $W^*$
of a $W^*$![]() -algebra $\mathcal {W}$
-algebra $\mathcal {W}$![]() , we denote by $W^*(t)$
, we denote by $W^*(t)$![]() the $W^*$
the $W^*$![]() -algebra generated by $t$
-algebra generated by $t$![]() and the unit element of $\mathcal {W},$
and the unit element of $\mathcal {W},$![]() that is, $W^*(t)$
that is, $W^*(t)$![]() is the $\sigma (\mathcal {W}, \mathcal {W}_{*})$
is the $\sigma (\mathcal {W}, \mathcal {W}_{*})$![]() -closure of $C^*(t)$
-closure of $C^*(t)$![]() , where $\mathcal {W}_{*}$
, where $\mathcal {W}_{*}$![]() is the predual of $\mathcal {W}$
is the predual of $\mathcal {W}$![]() (see [Reference Sakai34, Corollary 1.7.9]). Recall that every $W^*$
(see [Reference Sakai34, Corollary 1.7.9]). Recall that every $W^*$![]() -algebra always has a unit (see [Reference Sakai34, Sec. 1.7]).
-algebra always has a unit (see [Reference Sakai34, Sec. 1.7]).
Proposition 9.5 Let $\mathcal {W}$![]() be a $W^*$
be a $W^*$![]() -algebra with predual $\mathcal {W}_{*}$
-algebra with predual $\mathcal {W}_{*}$![]() and $t\in \mathcal {W}$
and $t\in \mathcal {W}$![]() be an expansion. Let $\{p_k\}_{k=0}^{\infty },$
be an expansion. Let $\{p_k\}_{k=0}^{\infty },$![]() $\{u_k\}_{k=0}^{\infty }$
$\{u_k\}_{k=0}^{\infty }$![]() and $\{v_k\}_{k=0}^{\infty }$
and $\{v_k\}_{k=0}^{\infty }$![]() be as in (9.2). Then
be as in (9.2). Then
(i) the sequence $\{p_k\}_{k=0}^{\infty }$
 is $\sigma (\mathcal {W}, \mathcal {W}_{*})$
is $\sigma (\mathcal {W}, \mathcal {W}_{*})$ -convergent to a projection $($
-convergent to a projection $($ i.e., a self-adjoint idempotent$)$
i.e., a self-adjoint idempotent$)$ of $\mathcal {W}$
of $\mathcal {W}$ denoted by $p_{\infty },$
denoted by $p_{\infty },$
(ii) $p_{\infty }$
 is the infimum of $\{p_k\}_{k=0}^{\infty }$
is the infimum of $\{p_k\}_{k=0}^{\infty }$ computed in the set of all self-adjoint elements of $\mathcal {W}$
computed in the set of all self-adjoint elements of $\mathcal {W}$ $($
$($ equivalently, in the set of all projections of $\mathcal {W}),$
equivalently, in the set of all projections of $\mathcal {W}),$
(iii) the sequences $\{u_k\}_{k=0}^{\infty }$
 and $\{v_k\}_{k=0}^{\infty }$
and $\{v_k\}_{k=0}^{\infty }$ are $\sigma (\mathcal {W}, \mathcal {W}_{*})$
are $\sigma (\mathcal {W}, \mathcal {W}_{*})$ -convergent to positive elements of $\mathcal {W}$
-convergent to positive elements of $\mathcal {W}$ denoted by $a$
denoted by $a$ and $b$
and $b$ , respectively.
, respectively.
Moreover, $t$![]() is an expansive element of $W^*(t)$
is an expansive element of $W^*(t)$![]() and the elements $t^{\prime }$
and the elements $t^{\prime }$![]() , $c_k$
, $c_k$![]() , $c_k^{-1}$
, $c_k^{-1}$![]() , $p_k$
, $p_k$![]() , $u_k,$
, $u_k,$![]() $v_k,$
$v_k,$![]() $p_{\infty },$
$p_{\infty },$![]() $a$
$a$![]() and $b$
and $b$![]() belong to $W^*(t).$
belong to $W^*(t).$![]()
Proof. (i)&(ii) By Proposition 9.3(i), $\{p_k\}_{k=0}^{\infty }$![]() is a uniformly bounded monotonically decreasing sequence of projections of $\mathcal {W}.$
is a uniformly bounded monotonically decreasing sequence of projections of $\mathcal {W}.$![]() It can be deduced from [Reference Sakai34, Lemma 1.7.4, Theorem 1.16.7 and Corollary 1.15.6] and [Reference Mlak29, Theorem 4.3.5] that the sequence $\{p_k\}_{k=0}^{\infty }$
It can be deduced from [Reference Sakai34, Lemma 1.7.4, Theorem 1.16.7 and Corollary 1.15.6] and [Reference Mlak29, Theorem 4.3.5] that the sequence $\{p_k\}_{k=0}^{\infty }$![]() is $\sigma (\mathcal {W},\mathcal {W}_{*})$
is $\sigma (\mathcal {W},\mathcal {W}_{*})$![]() -convergent to a projection of $\mathcal {W}$
-convergent to a projection of $\mathcal {W}$![]() , call it $p_{\infty }$
, call it $p_{\infty }$![]() , which is equal to the infimum of $\{p_k\}_{k=0}^{\infty }$
, which is equal to the infimum of $\{p_k\}_{k=0}^{\infty }$![]() computed in the set of all self-adjoint elements of $\mathcal {W}$
computed in the set of all self-adjoint elements of $\mathcal {W}$![]() . Consequently, $p_{\infty }$
. Consequently, $p_{\infty }$![]() coincides with the infimum of $\{p_k\}_{k=0}^{\infty }$
coincides with the infimum of $\{p_k\}_{k=0}^{\infty }$![]() computed in the set of all projections of $\mathcal {W}$
computed in the set of all projections of $\mathcal {W}$![]() .
.
(iii) It follows from [Reference Sakai34, Theorem 1.16.7] that there exists a faithful $W^*$![]() -representation $\pi \colon \mathcal {W} \to \mathcal {B}(\mathcal {H})$
-representation $\pi \colon \mathcal {W} \to \mathcal {B}(\mathcal {H})$![]() of $\mathcal {W}.$
of $\mathcal {W}.$![]() By [Reference Sakai34, Proposition 1.16.2], $\pi (\mathcal {W})$
By [Reference Sakai34, Proposition 1.16.2], $\pi (\mathcal {W})$![]() is $\sigma (\mathcal {B}(\mathcal {H}),\mathcal {B}(\mathcal {H})_{*})$
is $\sigma (\mathcal {B}(\mathcal {H}),\mathcal {B}(\mathcal {H})_{*})$![]() -closed. In turn, according to [Reference Sakai34, Proposition 1.15.1], $\pi (\mathcal {W})$
-closed. In turn, according to [Reference Sakai34, Proposition 1.15.1], $\pi (\mathcal {W})$![]() is SOT-closed. Since $\pi$
is SOT-closed. Since $\pi$![]() is an isometric $W^*$
is an isometric $W^*$![]() -homomorphism, we deduce from [Reference Shimorin36, Corollary 1.15.6] that for every $r\in (0,\infty )$
-homomorphism, we deduce from [Reference Shimorin36, Corollary 1.15.6] that for every $r\in (0,\infty )$![]() , the mapping
, the mapping
is continuous if $\mathcal {W}_r$![]() and $\pi (\mathcal {W})_r$
and $\pi (\mathcal {W})_r$![]() are equipped with the topologies $\sigma (\mathcal {W}, \mathcal {W}_{*})$
are equipped with the topologies $\sigma (\mathcal {W}, \mathcal {W}_{*})$![]() and $\sigma$
and $\sigma$![]() -WOT (the $\sigma$
-WOT (the $\sigma$![]() -weak operator topology), respectively. Because $\pi _r$
-weak operator topology), respectively. Because $\pi _r$![]() is a bijection, we infer from the Banach–Alaoglu theorem that $\pi _r$
is a bijection, we infer from the Banach–Alaoglu theorem that $\pi _r$![]() is a homeomorphism. By setting $T=\pi (t)$
is a homeomorphism. By setting $T=\pi (t)$![]() , it can be verified that
, it can be verified that
It follows from Proposition 8.7 that $\{\pi (v_k)\}_{k=0}^{\infty }$![]() converges in SOT, and consequently in $\sigma$
converges in SOT, and consequently in $\sigma$![]() -WOT to a positive operator $B\in \mathcal {B}(\mathcal {H})$
-WOT to a positive operator $B\in \mathcal {B}(\mathcal {H})$![]() . Since $\pi (\mathcal {W})$
. Since $\pi (\mathcal {W})$![]() is SOT-closed, there exists a (unique) positive element $b\in \mathcal {W}$
is SOT-closed, there exists a (unique) positive element $b\in \mathcal {W}$![]() such that $B=\pi (b).$
such that $B=\pi (b).$![]() By the uniform boundedness principle, there exists $r\in (0,\infty )$
By the uniform boundedness principle, there exists $r\in (0,\infty )$![]() such that $\pi (b), \pi (v_k) \in \pi (\mathcal {W})_r$
such that $\pi (b), \pi (v_k) \in \pi (\mathcal {W})_r$![]() for all $k\in \mathbb {Z}_+$
for all $k\in \mathbb {Z}_+$![]() . Since $\pi _r$
. Since $\pi _r$![]() is a homeomorphism, the sequence $\{v_k\}_{k=0}^{\infty }$
is a homeomorphism, the sequence $\{v_k\}_{k=0}^{\infty }$![]() converges in $\sigma (\mathcal {W}, \mathcal {W}_{*})$
converges in $\sigma (\mathcal {W}, \mathcal {W}_{*})$![]() to $b$
to $b$![]() . The same reasoning can be applied to the sequence $\{u_k\}_{k=0}^{\infty }$
. The same reasoning can be applied to the sequence $\{u_k\}_{k=0}^{\infty }$![]() .
.
The ‘moreover’ part is a direct consequence of the statements (i) and (iii), the ‘moreover’ part of Proposition 9.3 and [Reference Sakai34, Corollary 1.7.9]. This completes the proof.
After this preparation, we can give two equivalent definitions of the class $\mathcal {A}_{\infty }$![]() in the context of $W^*$
in the context of $W^*$![]() -algebras. The first one is patterned on the equivalence (i)$\Leftrightarrow$
-algebras. The first one is patterned on the equivalence (i)$\Leftrightarrow$![]() (iv) of Proposition 8.7.
(iv) of Proposition 8.7.
Definition 9.6 Let $\mathcal {W}$![]() be a $W^*$
be a $W^*$![]() -algebra. We say that $t\in \mathcal {W}$
-algebra. We say that $t\in \mathcal {W}$![]() is of class $\mathcal {A}_{\infty }$
is of class $\mathcal {A}_{\infty }$![]() if
if
(i) the spectral radius of $t$
 is at most $1$
is at most $1$ ,
,(ii) $t$
 is an expansion,
is an expansion,(iii) $p_{\infty } ((t^*t)^{-1} - t^{\prime } p_{\infty } t^{\prime *}) p_{\infty } \geqslant 0,$

where $p_{\infty }$![]() is as in Proposition 9.5.
is as in Proposition 9.5.
The second definition is based on the equivalence (i)$\Leftrightarrow$![]() (ii) of Proposition 8.7.
(ii) of Proposition 8.7.
Definition 9.7 Let $\mathcal {W}$![]() be a $W^*$
be a $W^*$![]() -algebra. We say that $t\in \mathcal {W}$
-algebra. We say that $t\in \mathcal {W}$![]() is of class $\mathcal {A}_{\infty }$
is of class $\mathcal {A}_{\infty }$![]() if
if
(i) the spectral radius of $t$
 is at most $1$
is at most $1$ ,
,(ii) $t$
 is an expansion,
is an expansion,(iii) $a\leqslant b,$

where $a$![]() and $b$
and $b$![]() are as in Proposition 9.5.
are as in Proposition 9.5.
Proof. Without loss of generality, we can assume that $t$![]() is an expansive element of $\mathcal {W}.$
is an expansive element of $\mathcal {W}.$![]() Let $\pi \colon \mathcal {W} \to \mathcal {B}(\mathcal {H})$
Let $\pi \colon \mathcal {W} \to \mathcal {B}(\mathcal {H})$![]() be a faithful $W^*$
be a faithful $W^*$![]() -representation of $\mathcal {W}$
-representation of $\mathcal {W}$![]() (see [Reference Sakai34, Theorem 1.16.7]). Set $T=\pi (t)$
(see [Reference Sakai34, Theorem 1.16.7]). Set $T=\pi (t)$![]() and $\mathcal {H}_u'=\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^{\prime n})$
and $\mathcal {H}_u'=\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^{\prime n})$![]() . By Proposition 9.5 and [Reference Sakai34, Corollary 1.15.6], $\{\pi (p_k)\}_{k=0}^{\infty }$
. By Proposition 9.5 and [Reference Sakai34, Corollary 1.15.6], $\{\pi (p_k)\}_{k=0}^{\infty }$![]() is $\sigma$
is $\sigma$![]() -WOT-convergent to $\pi (p_{\infty }).$
-WOT-convergent to $\pi (p_{\infty }).$![]() Since by (8.1), $\pi (p_k) = P_{{\mathcal {R}}(T^{\prime k})}$
Since by (8.1), $\pi (p_k) = P_{{\mathcal {R}}(T^{\prime k})}$![]() for every $k \in \mathbb {Z}_+,$
for every $k \in \mathbb {Z}_+,$![]() we see that $\pi (p_k) \searrow P_{\mathcal {H}_{u}'}$
we see that $\pi (p_k) \searrow P_{\mathcal {H}_{u}'}$![]() as $k\nearrow \infty$
as $k\nearrow \infty$![]() in SOT (see the proof of Proposition 8.7). As a consequence,
in SOT (see the proof of Proposition 8.7). As a consequence,
According to the proof of Proposition 9.5(iii), $\{\pi (v_k)\}_{k=0}^{\infty }$![]() is SOT-convergent to $\pi (b).$
is SOT-convergent to $\pi (b).$![]() By (9.5), the ‘moreover’ part of Proposition 8.7 and (9.6), we have
By (9.5), the ‘moreover’ part of Proposition 8.7 and (9.6), we have
The same reasoning applied to the sequence $\{u_k\}_{k=0}^{\infty }$![]() leads to the identity
leads to the identity
Clearly, the condition (iii) of Definition 9.7 is equivalent to $\pi (b-a) \geqslant 0,$![]() which by (9.7) and (9.8) is equivalent to the condition (iii) of Definition 9.6. This completes the proof.
which by (9.7) and (9.8) is equivalent to the condition (iii) of Definition 9.6. This completes the proof.
The following is the counterpart of Corollary 9.4 for elements of class $\mathcal {A}_{\infty }$![]() .
.
Corollary 9.9 If $\mathcal {W}$![]() is a $W^*$
is a $W^*$![]() -algebra and $t\in \mathcal {W},$
-algebra and $t\in \mathcal {W},$![]() then $t$
then $t$![]() is of class $\mathcal {A}_{\infty }$
is of class $\mathcal {A}_{\infty }$![]() if and only if $t$
if and only if $t$![]() is of class $\mathcal {A}_{\infty }$
is of class $\mathcal {A}_{\infty }$![]() as an element of $W^*(t).$
as an element of $W^*(t).$![]()
Proof. It follows from Proposition 9.5 and [Reference Conway17, Proposition VIII.1.14] that the infimum of $\{p_k\}_{k=0}^{\infty }$![]() computed in the set of all projections of $\mathcal {W}$
computed in the set of all projections of $\mathcal {W}$![]() coincides with the infimum of $\{p_k\}_{k=0}^{\infty }$
coincides with the infimum of $\{p_k\}_{k=0}^{\infty }$![]() computed in the set of all projections of $W^*(t).$
computed in the set of all projections of $W^*(t).$![]() Hence, by Theorem 9.8, we can apply Definition 9.6 and [Reference Conway17, Proposition VIII.1.14] again.
Hence, by Theorem 9.8, we can apply Definition 9.6 and [Reference Conway17, Proposition VIII.1.14] again.
One can see by applying Remark 1.2, Propositions 8.7 and 9.5 and [Reference Sakai34, Corollary 1.15.6] that Definitions 7.1 and 9.7 coincide for $k=\infty$![]() if $\mathcal {W} =\mathcal {B}(\mathcal {H})$
if $\mathcal {W} =\mathcal {B}(\mathcal {H})$![]() . Regarding Proposition 9.5(ii), it is worth pointing out that the property of being closed under the operation of taking infimum is one of the two basic properties characterizing $W^*$
. Regarding Proposition 9.5(ii), it is worth pointing out that the property of being closed under the operation of taking infimum is one of the two basic properties characterizing $W^*$![]() -algebras among $C^*$
-algebras among $C^*$![]() -algebras (cf. [Reference Kadison27, Definition 2.1]).
-algebras (cf. [Reference Kadison27, Definition 2.1]).