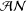Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ramesh, G.
2018.
Absolutely norm attaining paranormal operators.
Journal of Mathematical Analysis and Applications,
Vol. 465,
Issue. 1,
p.
547.
J., Ganesh
G., Ramesh
and
D., Sukumar
2018.
A characterization of absolutely minimum attaining operators.
Journal of Mathematical Analysis and Applications,
Vol. 468,
Issue. 1,
p.
567.
Venku Naidu, D
and
Ramesh, G
2019.
On absolutely norm attaining operators.
Proceedings - Mathematical Sciences,
Vol. 129,
Issue. 4,
DOUST, IAN
2019.
A NOTE ON POSITIVE OPERATORS.
Bulletin of the Australian Mathematical Society,
Vol. 100,
Issue. 1,
p.
129.
Bala, Neeru
and
Golla, Ramesh
2020.
Spectral properties of absolutely minimum attaining operators.
Banach Journal of Mathematical Analysis,
Vol. 14,
Issue. 3,
p.
630.
Bala, Neeru
and
Ramesh, G.
2021.
A representation of hyponormal absolutely norm attaining operators.
Bulletin des Sciences Mathématiques,
Vol. 171,
Issue. ,
p.
103020.
Bala, Neeru
Dhara, Kousik
Sarkar, Jaydeb
and
Sensarma, Aryaman
2021.
Idempotent, model, and Toeplitz operators attaining their norms.
Linear Algebra and its Applications,
Vol. 622,
Issue. ,
p.
150.
Ramesh, Golla
and
Osaka, Hiroyuki
2021.
On a subclass of norm attaining operators.
Acta Scientiarum Mathematicarum,
Vol. 87,
Issue. 1-2,
p.
247.
Kulkarni, S. H.
and
Ramesh, G.
2021.
Absolutely minimum attaining closed operators.
The Journal of Analysis,
Vol. 29,
Issue. 2,
p.
473.
Böttcher, Albrecht
and
Spitkovsky, Ilya M.
2021.
The norm attainment problem for functions of projections.
Archiv der Mathematik,
Vol. 117,
Issue. 4,
p.
397.
Dhara, Kousik
and
Dym, Harry
2022.
Norms of Basic Operators in Vector Valued Model Spaces and de Branges Spaces.
Integral Equations and Operator Theory,
Vol. 94,
Issue. 4,
Ramesh, G.
and
Osaka, H.
2022.
On operators which attain their norm on every reducing subspace.
Annals of Functional Analysis,
Vol. 13,
Issue. 2,
Ramesh, G.
and
Sequeira, Shanola S.
2022.
Absolutely norm attaining Toeplitz and absolutely minimum attaining Hankel operators.
Journal of Mathematical Analysis and Applications,
Vol. 516,
Issue. 1,
p.
126497.
Ramesh, Golla
and
Sequeira, Shanola S.
2023.
Absolutely minimum attaining Toeplitz and absolutely norm attaining Hankel operators.
Comptes Rendus. Mathématique,
Vol. 361,
Issue. G6,
p.
973.
Ramesh, G.
and
Sequeira, Shanola S.
2023.
On the closure of absolutely norm attaining operators.
Linear and Multilinear Algebra,
Vol. 71,
Issue. 18,
p.
2894.
Ramesh, G.
Osaka, H.
Udagawa, Y.
and
Yamazaki, T.
2023.
Stability of $${\cal A}{\cal N}$$-Operators under Functional Calculus.
Analysis Mathematica,
Vol. 49,
Issue. 3,
p.
825.
Bala, Neeru
2023.
Representation and normality of $$*$$-paranormal absolutely norm attaining operators.
Acta Scientiarum Mathematicarum,
Vol. 89,
Issue. 1-2,
p.
167.
Golla, Ramesh
Osaka, Hiroyuki
Udagawa, Yoichi
and
Yamazaki, Takeaki
2023.
Stability of AN-property for the induced Aluthge transformations.
Linear Algebra and its Applications,
Vol. 678,
Issue. ,
p.
206.
Ramesh, G.
and
Sequeira, S. S.
2024.
Representation and normality of hyponormal operators in the closure of $$\mathcal{AN}$$-operators.
Acta Mathematica Hungarica,
Vol. 174,
Issue. 2,
p.
341.
John, Tiju Cherian
Kumar, V. B. Kiran
and
Tonny, Anmary
2024.
An order relation between eigenvalues and symplectic eigenvalues of a class of infinite-dimensional operators.
Quantum Studies: Mathematics and Foundations,
Vol. 11,
Issue. 3,
p.
549.