No CrossRef data available.
Elliptic problems for a Douglis–Nirenberg system over ℝn and over an exterior subregion
Published online by Cambridge University Press: 22 March 2016
Extract
We consider both a problem over ℝn and a boundary problem over an exterior subregion for a Douglis–Nirenberg system of differential operators under limited smoothness assumptions as well as under the assumption of parameter ellipticity in a closed sector Ꮭ in the complex plane with vertex at the origin. We pose each problem on an Lp Sobolev space setting, 1 < p < ∞, and denote by 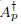 the operator induced in this setting by the problem over ℝn and by Ap the operator induced in this setting by the boundary problem under null boundary conditions. We then derive results pertaining to the Fredholm theory for each of these operators for values of the spectral parameter λ lying in Ꮭ as well as results for these values of λ pertaining to the invariance of their Fredholm domains with p.
the operator induced in this setting by the problem over ℝn and by Ap the operator induced in this setting by the boundary problem under null boundary conditions. We then derive results pertaining to the Fredholm theory for each of these operators for values of the spectral parameter λ lying in Ꮭ as well as results for these values of λ pertaining to the invariance of their Fredholm domains with p.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 146 , Issue 3 , June 2016 , pp. 579 - 594
- Copyright
- Copyright © Royal Society of Edinburgh 2016

