Article contents
POLISH MODELS AND SOFIC ENTROPY
Published online by Cambridge University Press: 18 January 2016
Abstract
We deduce properties of the Koopman representation of a positive entropy probability measure-preserving action of a countable, discrete, sofic group. Our main result may be regarded as a‘representation-theoretic’ version of Sinaǐ’s factor theorem. We show that probability measure-preserving actions with completely positive entropy of an infinite sofic group must be mixing and, if the group is nonamenable, have spectral gap. This implies that if 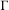 $\unicode[STIX]{x1D6E4}$ is a nonamenable group and
$\unicode[STIX]{x1D6E4}$ is a nonamenable group and 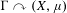 $\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ is a probability measure-preserving action which is not strongly ergodic, then no action orbit equivalent to
$\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ is a probability measure-preserving action which is not strongly ergodic, then no action orbit equivalent to 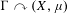 $\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ has completely positive entropy. Crucial to these results is a formula for entropy in the presence of a Polish, but a priori noncompact, model.
$\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ has completely positive entropy. Crucial to these results is a formula for entropy in the presence of a Polish, but a priori noncompact, model.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 2 , April 2018 , pp. 241 - 275
- Copyright
- © Cambridge University Press 2016
References
- 7
- Cited by

