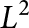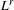Refine listing
Actions for selected content:
128 results in 76Dxx
On travelling wave solutions of a model of a liquid film flowing down a fibre
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 12 August 2021, pp. 864-893
-
- Article
- Export citation
On regularity properties of a surface growth model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 1869-1892
- Print publication:
- December 2021
-
- Article
- Export citation
Two-phase Stokes flow by capillarity in full 2D space: an approach via hydrodynamic potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 1815-1845
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
Global well-posedness and decay estimates of strong solutions to the nonhomogeneous Boussinesq equations for magnetohydrodynamics convection
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1543-1567
- Print publication:
- October 2021
-
- Article
- Export citation
ADAPTIVE GRID REFINEMENT USING THE GENERALISED FINITE-DIFFERENCE METHOD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 11 September 2020, p. 349
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
A Note on the Vanishing Viscosity Limit in the Yudovich Class
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 112-122
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
When a small thin two-dimensional body enters a viscous wall layer
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 1002-1028
-
- Article
- Export citation
About a cavitation model including bubbles in thin film lubrication: A first mathematical analysis
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 14 October 2019, pp. 828-853
-
- Article
- Export citation
Potential flow over a submerged rectangular obstacle: Consequences for initiation of boulder motion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 646-681
-
- Article
- Export citation
ON LOCAL ENERGY DECAY ESTIMATE OF THE OSEEN SEMIGROUP IN TWO DIMENSIONS AND ITS APPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 01 July 2019, pp. 859-891
- Print publication:
- May 2021
-
- Article
- Export citation
ON STABILITY OF PHYSICALLY REASONABLE SOLUTIONS TO THE TWO-DIMENSIONAL NAVIER–STOKES EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 16 May 2019, pp. 517-568
- Print publication:
- March 2021
-
- Article
- Export citation
ON THE TOPOGRAPHY-DRIVEN VORTICITY PRODUCTION IN SHALLOW LAKES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 148-160
-
- Article
-
- You have access
- Export citation
Regularity results for the 2D critical Oldroyd-B model in the corotational case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1871-1913
- Print publication:
- August 2020
-
- Article
- Export citation
Long-time asymptotic expansions for Navier-Stokes equations with power-decaying forces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 569-606
- Print publication:
- April 2020
-
- Article
- Export citation
A RAYLEIGH–RITZ METHOD FOR NAVIER–STOKES FLOW THROUGH CURVED DUCTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 1-22
-
- Article
-
- You have access
- Export citation
STOCHASTIC NAVIER–STOKES EQUATIONS ON 2D ROTATING SPHERES WITH STABLE LÉVY NOISE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 344-345
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
NONSYMMETRIC BRANCHING OF FLUID FLOWS IN 3D VESSELS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 June 2018, pp. 533-561
-
- Article
-
- You have access
- Export citation
A POROUS VISCOELASTIC MODEL FOR THE CELL CYTOSKELETON
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 25 May 2018, pp. 472-498
-
- Article
-
- You have access
- Export citation
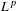 $L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
$L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 10 April 2018, pp. 231-258
- Print publication:
- January 2020
-
- Article
- Export citation
Topology Optimization of Capillary, Two-Phase Flow Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 31 October 2017, pp. 1413-1438
- Print publication:
- November 2017
-
- Article
- Export citation