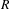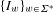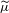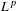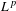Contents
Research Article
SUR L’ÉTUDE DE L’ENTROPIE DESAPPLICATIONS MÉROMORPHES
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 1-19
-
- Article
- Export citation
GENERALIZED THOM SPECTRA AND THEIR TOPOLOGICAL HOCHSCHILD HOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 21-64
-
- Article
- Export citation
RANDOM SPARSE SAMPLING IN A GIBBS WEIGHTED TREE AND PHASE TRANSITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 May 2018, pp. 65-116
-
- Article
- Export citation
THE CRAMÉR–WOLD THEOREM ON QUADRATIC SURFACES AND HEISENBERG UNIQUENESS PAIRS
- Part of:
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 117-135
-
- Article
- Export citation
GENERALISED DIVISOR SUMS OF BINARY FORMS OVER NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 16 November 2017, pp. 137-173
-
- Article
- Export citation
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2018, pp. 175-208
-
- Article
- Export citation
CANONICALLY FIBERED SURFACES OF GENERAL TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2018, pp. 209-229
-
- Article
-
- You have access
- Export citation
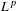 $L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
$L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2018, pp. 231-258
-
- Article
- Export citation
EQUIVALENT NORMS WITH AN EXTREMELY NONLINEABLE SET OF NORM ATTAINING FUNCTIONALS
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2018, pp. 259-279
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 19 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 December 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JMJ volume 19 Issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 December 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation