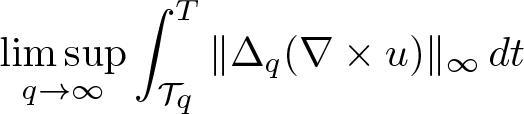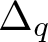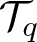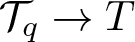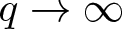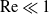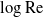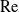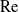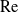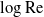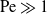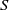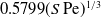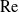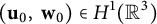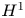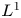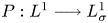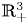Refine listing
Actions for selected content:
128 results in 76Dxx
Ill-posedness issue on the Oldroyd-B model in the critical Besov spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-20
-
- Article
- Export citation
Well-posedness of Naiver–Stokes equations in logarithmic Q spaces covering
 $BMO^{-1}$ and its fractional counterpart
$BMO^{-1}$ and its fractional counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regularity criteria for the 3D Navier–Stokes and MHD equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 June 2025, pp. 1-35
-
- Article
- Export citation
3D Navier–Stokes–Voigt equations with damping and double delays on unbounded domains: Well-posedness, pullback attractors, and limit measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1-39
-
- Article
- Export citation
Well-posedness for the 3-D generalized micropolar system in critical Fourier–Besov–Morrey spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 891-907
- Print publication:
- September 2025
-
- Article
- Export citation
CAPILLARY LEVELLING OF THIN LIQUID FILMS OF POWER-LAW RHEOLOGY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 62-76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large Péclet number forced convection from a circular wire in a uniform stream: hybrid approximations at small Reynolds numbers
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 16 April 2024, pp. 823-834
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The non-autonomous Navier–Stokes–Brinkman–Forchheimer equation with Dirichlet boundary conditions: dissipativity, regularity, and attractors
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2023, pp. 352-393
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability of axisymmetric flow in thermocapillary liquid bridges: Kinetic and thermal energy budgets for two-phase flow with temperature-dependent material properties
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 07 July 2023, pp. 267-293
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PILOT-WAVE HYDRODYNAMICS: QUANTISATION OF PARTIAL INTEGRABILITY FROM A NONLINEAR INTEGRO-DIFFERENTIAL EQUATION OF THE SECOND ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 472-479
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on energy equality for the fractional Navier-Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 February 2023, pp. 201-208
- Print publication:
- February 2024
-
- Article
- Export citation
Global existence of the strong solution to the 3D incompressible micropolar equations with fractional partial dissipation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 13 September 2022, pp. 1516-1539
- Print publication:
- October 2023
-
- Article
- Export citation
Stability and exponential decay for magnetohydrodynamic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 853-880
- Print publication:
- June 2023
-
- Article
- Export citation
A DYNAMICAL STUDY OF SALINE PLUMES IN DESALINATION OUTFALLS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 01 March 2022, pp. 523-524
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
Leidenfrost levitation of a spherical particle above a liquid bath: Evolution of the vapour-film morphology with particle size
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 17 February 2022, pp. 1117-1169
-
- Article
- Export citation
Large deviation principles of 2D stochastic Navier–Stokes equations with Lévy noises
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 18 November 2021, pp. 19-67
- Print publication:
- February 2023
-
- Article
- Export citation
Decay properties for the incompressible Navier-Stokes flows in a half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1509-1532
- Print publication:
- December 2022
-
- Article
- Export citation
A REVIEW OF ONE-PHASE HELE-SHAW FLOWS AND A LEVEL-SET METHOD FOR NONSTANDARD CONFIGURATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 23 September 2021, pp. 269-307
-
- Article
- Export citation
Global regularity criterion for the dissipative systems modelling electrohydrodynamics involving the middle eigenvalue of the strain tensor
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 1277-1290
- Print publication:
- October 2022
-
- Article
- Export citation
On the Cauchy problem associated with the Brinkman flow in
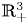 $\mathbb {R}_{+}^{3}$
$\mathbb {R}_{+}^{3}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 1089-1108
- Print publication:
- October 2022
-
- Article
- Export citation