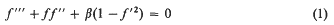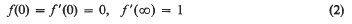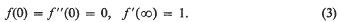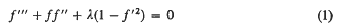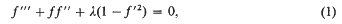Refine listing
Actions for selected content:
128 results in 76Dxx
A note on the motion of a closely fitting plug along a fluid-filled tube
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-70
- Print publication:
- June 1977
-
- Article
- Export citation
Pipeflows distorted by non-symmetric indentation or branching
- Part of
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-83
- Print publication:
- June 1976
-
- Article
- Export citation
Note on the slow rotation of a concave spherical lens or bowl in two immiscible semi-infinite viscous fluids
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-154
- Print publication:
- June 1974
-
- Article
- Export citation
On the slow viscous rotation of a body straddling the interface between two immiscible semi-infinite fluids
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 175-196
- Print publication:
- December 1973
-
- Article
- Export citation
On some solutions of the Falkner-Skan equation
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-83
- Print publication:
- June 1972
-
- Article
- Export citation
Reverse flow solutions of the Falkner-Skan equation for λ > 1
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-138
- Print publication:
- June 1972
-
- Article
- Export citation
On the uniqueness of solutions of the Falkner-Skan equation
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-133
- Print publication:
- June 1972
-
- Article
- Export citation
On the non-linear response of a marginally unstable plane parallel flow to a three-dimensional disturbance
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 219-239
- Print publication:
- December 1971
-
- Article
- Export citation