If the closed wire frame of a soap film having the shape of a Möbius strip is pulled apart and gradually deformed into a planar circle, the soap film transforms into a two-sided orientable surface. In the presence of a finite-time twist singularity, which changes the linking number of the film's Plateau border and the centreline of the wire, the topological transformation involves the collapse of the film toward the wire. In contrast to experimental studies of this process reported elsewhere, we use a numerical approach based on the immersed boundary method, which treats the soap film as a massless membrane in a Navier-Stokes fluid. In addition to known effects, we discover vibrating motions of the film arising after the topological change is completed, similar to the vibration of a circular membrane.

We present a moving-least-square immersed boundary method for solving viscous incompressible flow involving deformable and rigid boundaries on a uniform Cartesian grid. For rigid boundaries, noslip conditions at the rigid interfaces are enforced using the immersed-boundary direct-forcing method. We propose a reconstruction approach that utilizes moving least squares (MLS) method to reconstruct the velocity at the forcing points in the vicinity of the rigid boundaries. For deformable boundaries, MLS method is employed to construct the interpolation and distribution operators for the immersed boundary points in the vicinity of the rigid boundaries instead of using discrete delta functions. The MLS approach allows us to avoid distributing the Lagrangian forces into the solid domains as well as to avoid using the velocity of points inside the solid domains to compute the velocity of the deformable boundaries. The present numerical technique has been validated by several examples including a Poiseuille flow in a tube, deformations of elastic capsules in shear flow and dynamics of red-blood cell in microfluidic devices.

The present paper follows our previous work [Yang et al., Phys. Rev. E, 90 (2014), 063011] in which the bending modes of a symmetric flexible fiber in viscous flows were studied by using a coupling approach of smoothed particle hydrodynamics (SPH) and element bending group (EBG). It was shown that a symmetric flexible fiber can undergo four different bending modes including stable U-shape, slight swing, violent flapping and stable closure modes. For an asymmetric flexible fiber, the bending modes can be different. This paper numerically studies the fiber shape, flow field and fluid drag of an asymmetric flexible fiber immersed in a viscous fluid flow by using the SPH-EBG coupling method. An asymmetric number is defined to describe the asymmetry of a flexible fiber. The effects of the asymmetric number on the fiber shape, flow field and fluid drag are investigated.

The Stokes axisymmetric flow of an incompressible viscous fluid past a micropolar fluid spheroid whose shape deviates slightly from that of a sphere is studied analytically. The boundary conditions used are the vanishing of the normal velocities, the continuity of the tangential velocities, continuity of shear stresses and spin-vorticity relation at the surface of the spheroid. The hydrodynamic drag force acting on the fluid spheroid is calculated. An exact solution of the problem is obtained to the first order in the small parameter characterizing the deformation. It is observed that due to increase spin parameter value, the drag coefficient decreases. Well known results are deduced and comparisons are made with classical viscous fluid and micropolar fluid.

A numerical method is presented for the computation of externally forced Stokes flows bounded by the plane z=0 and satisfying periodic boundary conditions in the x and y directions. The motivation for this work is the simulation of flows generated by cilia, which are hair-like structures attached to the surface of cells that generate flows through coordinated beating. Large collections of cilia on a surface can be modeled using a doubly-periodic domain. The approach presented here is to derive a regularized version of the fundamental solution of the incompressible Stokes equations in Fourier space for the periodic directions and physical space for the z direction. This analytical expression for û(k,m;z) can then be used to compute the fluid velocity u(x,y,z) via a two-dimensional inverse fast Fourier transform for any fixed value of z. Repeating the computation for multiple values of z leads to the fluid velocity on a uniform grid in physical space. The zero-flow condition at the plane z=0 is enforced through the use of images. The performance of the method is illustrated by numerical examples of particle transport by nodal cilia, which verify optimal particle transport for parameters consistent with previous studies. The results also show that for two cilia in the periodic box, out-of-phase beating produces considerablemore particle transport than in-phase beating.

In this article, we study theoretically and numerically the interaction of a vortex induced by a rotating cylinder with a perpendicular plane. We show the existence of weak solutions to the swirling vortex models by using the Hopf extension method, and by an elegant contradiction argument, respectively. We demonstrate numerically that the model could produce phenomena of swirling vortex including boundary layer pumping and two-celled vortex that are observed in potential line vortex interacting with a plane and in a tornado.

Almost all schemes existed in the literature to solve the Lattice Boltzmann Equation like stream & collide, finite difference, finite element, finite volume schemes are explicit. However, it is known fact that implicit methods utilizes better stability and faster convergence compared to the explicit methods. In this paper, a method named herein as Implicit Finite Volume Lattice Boltzmann Method (IFVLBM) for incompressible laminar and turbulent flows is proposed and it is applied to some 2D benchmark test cases given in the literature. Alternating Direction Implicit, an approximate factorization method is used to solve the obtained algebraic system. The proposed method presents a very good agreement for all the validation cases with the literature data. The proposed method shows good stability characteristics, the CFL number is eased. IFVLBM has about 2 times faster convergence rate compared with Implicit-Explicit Runge Kutta method even though it possesses a computational burden from the solution of algebraic systems of equations.

Vortex and vorticity are two correlated but fundamentally different concepts which have been the central issues in fluid mechanics research. Vorticity has rigorous mathematical definition (curl of velocity), but no clear physical meaning. Vortex has clear physical meaning (rotation) but no rigorous mathematical definition. For a long time, many people treat them as a same thing. However, based on our high-order direct numerical simulation (DNS), we found that first, “vortex” is not “vorticity tube” or “vortex tube” which is widely defined as a bundle of vorticity lines without any vorticity line leak. Actually, vortex is an open area for vorticity line penetration. Second, vortex is not necessarily congregation of vorticity lines, but dispersion in many 3-dimensional cases. Some textbooks say that vortex cannot end inside the flow field but must end on the solid wall (and/or boundaries). Our DNS observation and many other numerical results show almost all vortices are ended inside the flow field. Finally, a more theoretical study shows that neither vortex nor vorticity line can attach to the solid wall and they must be detached from the wall.

In this paper, we study an exponential time differencing method for solving the gauge system of incompressible viscous flows governed by Stokes or Navier-Stokes equations. The momentum equation is decoupled from the kinematic equation at a discrete level and is then solved by exponential time stepping multistep schemes in our approach. We analyze the stability of the proposed method and rigorously prove that the first order exponential time differencing scheme is unconditionally stable for the Stokes problem. We also present a compact representation of the algorithm for problems on rectangular domains, which makes FFT-based solvers available for the resulting fully discretized system. Various numerical experiments in two and three dimensional spaces are carried out to demonstrate the accuracy and stability of the proposed method.

This paper describes an adaptive preconditioner for numerical continuation of incompressible Navier–Stokes flows based on Stokes preconditioning [42] which has been used successfully in studies of pattern formation in convection. The preconditioner takes the form of the Helmholtz operator I–ΔtL which maps the identity (no preconditioner) for Δt≪1 to Laplacian preconditioning for Δt≫1. It is built on a first order Euler time-discretization scheme and is part of the family of matrix-free methods. The preconditioner is tested on two fluid configurations: three-dimensional doubly diffusive convection and a two-dimensional projection of a shear flow. 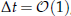In the former case, it is found that Stokes preconditioning is more efficient for , away from the values used in the literature. In the latter case, the simple use of the preconditioner is not sufficient and it is necessary to split the system of equations into two subsystems which are solved simultaneously using two different preconditioners, one of which is parameter dependent. Due to the nature of these applications and the flexibility of the approach described, this preconditioner is expected to help in a wide range of applications.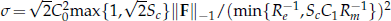

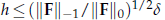A lattice Boltzmann method is utilized for governing equations which control phase separation of binary fluids with reversible chemical reaction in presence of a shear flow in this paper. We first present the morphology modeling of sheared binary fluids with reversible chemical reaction. We then validate the model by taking the unsheared binary fluids as an example. It is found that the results fit well with the references. The paper shows structures of the sheared system and gives the detailed analysis for the morphology of sheared binary fluids with reversible chemical reaction. The phase separation of the domain structures with different chemical reaction rates is discussed. Through simulations of the sheared binary fluids, two interesting phenomena are observed, which do not exist in a binary mixture without reversible chemical reaction. One is that the same results appear in both low and high viscosity, and the other is that the domain growth exponent with both low and high viscosities presents wave due to the competition of the viscosity and phase separation. In addition, we find that the finite size effects resulting in the growth exponent decreasing appear faster than that of the unsheared blend at a large time when the size of domains is comparable with the lattice size.

Pressure-correction projection finite element methods (FEMs) are proposed to solve nonstationary natural convection problems in this paper. The first-order and second-order backward difference formulas are applied for time derivative, the stability analysis and error estimates of the semi-discrete schemes are presented using energy method. Compared with characteristic variational multiscale FEM, pressure-correction projection FEMs are more efficient and unconditionally energy stable. Ample numerical results are presented to demonstrate the effectiveness of the pressure-correction projection FEMs for solving these problems.

The lattice Boltzmann method is employed to simulate the steady flow in a two-dimensional lid-driven semi-elliptical cavity. Reynolds number (Re) and vertical-to-horizontal semi-axis ratio (D) are in the range of 500-5000 and 0.1-4, respectively. The effects of Re and D on the vortex structure and pressure field are investigated, and the evolutionary features of the vortex structure with Re and D are analyzed in detail. Simulation results show that the vortex structure and its evolutionary features significantly depend on Re and D. The steady flow is characterized by one vortex in the semi-elliptical cavity when both Re and D are small. As Re increases, the appearance of the vortex structure becomes more complex. When D is less than 1, increasing D makes the large vortexes more round, and the evolution of the vortexes with D becomes more complex with increasing Re. When D is greater than 1, the steady flow consists of a series of large vortexes which superimpose on each other. As Re and D increase, the number of the large vortexes increases. Additionally, a small vortex in the upper-left corner of the semi-elliptical cavity appears at a large Re and its size increases slowly as Re increases. The highest pressures appear in the upper-right corner and the pressure changes drastically in the upper-right region of the cavity. The total pressure differences in the semi-elliptical cavity with a fixed D decrease with increasing Re. In the region of themain vortex, the pressure contours nearly coincide with the streamlines, especially for the cavity flow with a large Re.

In this paper, we present an efficient rescaling scheme for computing the long-time dynamics of expanding interfaces. The idea is to design an adaptive time-space mapping such that in the new time scale, the interfaces evolves logarithmically fast at early growth stage and exponentially fast at later times. The new spatial scale guarantees the conservation of the area/volume enclosed by the interface. Compared with the original rescaling method in [J. Comput. Phys. 225(1) (2007) 554–567], this adaptive scheme dramatically improves the slow evolution at early times when the size of the interface is small. Our results show that the original three-week computation in [J. Comput. Phys. 225(1) (2007) 554–567] can be reproduced in about one day using the adaptive scheme. We then present the largest and most complicated Hele-Shaw simulation up to date.

In this article, by applying the Stokes projection and an orthogonal projection with respect to curl and div operators, some new error estimates of finite element method (FEM) for the stationary incompressible magnetohydrodynamics (MHD) are obtained. To our knowledge, it is the first time to establish the error bounds which are explicitly dependent on the Reynolds numbers, coupling number and mesh size. On the other hand, The uniform stability and convergence of an Oseen type finite element iterative method for MHD with respect to high hydrodynamic Reynolds number Re and magnetic Reynolds number Rm, or small δ=1–σ with

(C0, C1 are constants depending only on Ω and F is related to the source terms of equations) are analyzed under the condition that . Finally, some numerical tests are presented to demonstrate the effectiveness of this algorithm.

In this paper, the problem of magnetohydrodynamics (MHD) boundary layer flow of nanofluid with heat and mass transfer through a porous media in the presence of thermal radiation, viscous dissipation and chemical reaction is studied. Three types of nanofluids, namely Copper (Cu)-water, Alumina (Al 2 O 3)-water and Titanium Oxide (TiO 2)-water are considered. The governing set of partial differential equations of the problem is reduced into the coupled nonlinear system of ordinary differential equations (ODEs) by means of similarity transformations. Finite element solution of the resulting system of nonlinear differential equations is obtained using continuous Galerkin-Petrov discretization together with the well-known shooting technique. The obtained results are validated using MATLAB “bvp4c” function and with the existing results in the literature. Numerical results for the dimensionless velocity, temperature and concentration profiles are obtained and the impact of various physical parameters such as the magnetic parameter M, solid volume fraction of nanoparticles 𝜙 and type of nanofluid on the flow is discussed. The results obtained in this study confirm the idea that the finite element method (FEM) is a powerful mathematical technique which can be applied to a large class of linear and nonlinear problems arising in different fields of science and engineering.

An investigation of natural convective flow and heat transfer inside a three dimensional rectangular cavity containing an array of discrete heat sources is carried out. The array consists of a row and columnwise regular arrangement of identical square shaped isoflux discrete heaters and is flush mounted on a vertical wall of the cavity. A symmetrical isothermal sink condition is maintained by cooling the cavity uniformly from either the opposite wall or the side walls or the top and bottom walls. The other walls of the cavity are maintained adiabatic. A finite volume method based on the SIMPLE algorithm and the power law scheme is used to solve the conservation equations. The parametric study covers the influence of pertinent parameters such as the Rayleigh number, the Prandtl number, side aspect ratio of the cavity and cavity heater ratio. A detailed fluid flow and heat transfer characteristics for the three cases are reported in terms of isothermal and velocity vector plots and Nusselt numbers. In general it is found that the overall heat transfer rate within the cavity for Ra=107 is maximum when the side aspect ratio of the cavity lies between 1.5 and 2. A more complex and peculiar flow pattern is observed in the presence of top and bottom cold walls which in turn introduces hot spots on the adiabatic walls. Their location and size are highly sensitive to the side aspect ratio of the cavity and hence offers more effective ways for passive heat removal.

In this work, we study numerical methods for a coupled fluid-porous media flow model. The model consists of Stokes equations and Darcy's equations in two neighboring subdomains, coupling together through certain interface conditions. The weak form for the coupled model is of saddle point type. A mortar finite element method is proposed to approximate the weak form of the coupled problem. In our method, nonconforming Crouzeix-Raviart elements are applied in the fluid subdomain and the lowest order Raviart-Thomas elements are applied in the porous media subdomain; Meshes in different subdomains are allowed to be nonmatching on the common interface; Interface conditions are weakly imposed via adding constraint in the definition of the finite element space. The well-posedness of the discrete problem and the optimal error estimate for the proposed method are established. Numerical experiments are also given to confirm the theoretical results.

The motion and rotation of an ellipsoidal particle inside square tubes and rectangular tubes with the confinement ratio R/a∈(1.0,4.0) are studied by the lattice Boltzmann method (LBM), where R and a are the radius of the tube and the semi-major axis length of the ellipsoid, respectively. The Reynolds numbers (Re) up to 50 are considered. For the prolate ellipsoid inside square and rectangular tubes, three typical stable motion modes which depend on R/a are identified, namely, the kayaking mode, the tumbling mode, and the log-rolling mode are identified for the prolate spheroid. The diagonal plane strongly attracts the particle in square tubes with 1.2≤R/a<3.0. To explore the mechanism, some constrained cases are simulated. It is found that the tumbling mode in the diagonal plane is stable because the fluid force acting on the particle tends to diminish the small displacement and will bring it back to the plane. Inside rectangular tubes the particle will migrate to a middle plane between short walls instead of the diagonal plane. Through the comparisons between the initial unstable equilibrium motion state and terminal stable mode, it is seems that the particle tend to adopt the mode with smaller kinetic energy.