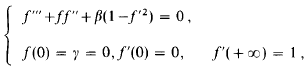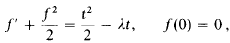Refine listing
Actions for selected content:
128 results in 76Dxx
A note on Stokes flow due to a line rotlet
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-132
- Print publication:
- June 1995
-
- Article
- Export citation
The rotation of two circular cylinders in a viscous fluid
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-126
- Print publication:
- June 1995
-
- Article
- Export citation
Concentration-cancellation and Hardy spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 94-99
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Eccentric oscillations of a circular cylinder in a viscous fluid
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 187-202
- Print publication:
- December 1993
-
- Article
- Export citation
On the starting process of strongly nonlinear vortex/Rayleigh-wave interactions
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-29
- Print publication:
- June 1993
-
- Article
- Export citation
Oscillating viscous flows: II superposed oscillations
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-216
- Print publication:
- December 1991
-
- Article
- Export citation
The rotation of two circular cylinders in a viscous fluid
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-66
- Print publication:
- June 1991
-
- Article
- Export citation
Görtler vortices in growing boundary layers: The leading edge receptivity problem, linear growth and the nonlinear breakdown stage
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-189
- Print publication:
- December 1990
-
- Article
- Export citation
Nonlinear interaction of near-planar TS waves and longitudinal vortices in boundary-layer transition
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 262-289
- Print publication:
- December 1989
-
- Article
- Export citation
Finite-time break-up can occur in any unsteady interacting boundary layer
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 256-273
- Print publication:
- December 1988
-
- Article
- Export citation
A note on the Jeffery paradox
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-186
- Print publication:
- December 1987
-
- Article
- Export citation
Complete breakdown of an unsteady interactive boundary layer (over a surface distortion or in a liquid layer)
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 86-100
- Print publication:
- June 1987
-
- Article
- Export citation
Two-dimensional Stokes flows with cylinders and line singularities
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-75
- Print publication:
- June 1984
-
- Article
- Export citation
On hypersonic self-induced separation, hydraulic jumps and boundary layers with algebraic growth
- Part of
-
- Journal:
- Mathematika / Volume 30 / Issue 1 / June 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-93
- Print publication:
- June 1983
-
- Article
- Export citation
Further solutions of the Falkner–Skan equation for β = – 1 and γ = 0
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-248
- Print publication:
- December 1982
-
- Article
- Export citation
Low-Reynolds-number flow between converging spheres
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-66
- Print publication:
- June 1982
-
- Article
- Export citation
Instability of flow through pipes of general cross-section, Part 1
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 187-210
- Print publication:
- December 1979
-
- Article
- Export citation
Mass transport induced by standing interfacial waves
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 224-235
- Print publication:
- December 1979
-
- Article
- Export citation
Instability of flow through pipes of general cross-section, Part 2
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 211-223
- Print publication:
- December 1979
-
- Article
- Export citation
Laminar flow over a small unsteady hump on a flat plate
- Part of
-
- Journal:
- Mathematika / Volume 25 / Issue 1 / June 1978
- Published online by Cambridge University Press:
- 26 February 2010, pp. 24-35
- Print publication:
- June 1978
-
- Article
- Export citation