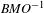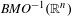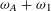Refine listing
Actions for selected content:
128 results in 76Dxx
Vortical Flow Structure in the Wake of an Estate Car
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 15 October 2015, pp. 881-900
- Print publication:
- October 2015
-
- Article
- Export citation
Direct-Forcing Immersed Boundary Method for Mixed Heat Transfer
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 15 October 2015, pp. 1072-1094
- Print publication:
- October 2015
-
- Article
- Export citation
Dynamics and Instability of a Vortex Ring Impinging on a Wall
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 15 October 2015, pp. 1122-1146
- Print publication:
- October 2015
-
- Article
- Export citation
Construction, Analysis and Application of Coupled Compact Difference Scheme in Computational Acoustics and Fluid Flow Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 15 October 2015, pp. 957-984
- Print publication:
- October 2015
-
- Article
- Export citation
Three-Dimensional Lattice Boltzmann Flux Solver and Its Applications to Incompressible Isothermal and Thermal Flows
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 14 September 2015, pp. 593-620
- Print publication:
- September 2015
-
- Article
- Export citation
The Hele-Shaw flow and moduli of holomorphic discs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 18 August 2015, pp. 2301-2328
- Print publication:
- December 2015
-
- Article
- Export citation
Numerical Simulations of Particle Sedimentation Using the Immersed Boundary Method
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 2 / August 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 380-416
- Print publication:
- August 2015
-
- Article
- Export citation
KELVIN–HELMHOLTZ CREEPING FLOW AT THE INTERFACE BETWEEN TWO VISCOUS FLUIDS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 02 July 2015, pp. 317-358
-
- Article
-
- You have access
- Export citation
ON THE WELL-POSEDNESS OF PARABOLIC EQUATIONS OF NAVIER–STOKES TYPE WITH
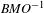 $\mathit{BMO}^{-1}$ DATA
$\mathit{BMO}^{-1}$ DATA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 27 April 2015, pp. 947-985
- Print publication:
- November 2017
-
- Article
- Export citation
MOVING STONE IN THE HELE-SHAW FLOW
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 08 April 2015, pp. 457-474
- Print publication:
- May 2015
-
- Article
- Export citation
ON A SINGULAR INITIAL-VALUE PROBLEM FOR THE NAVIER–STOKES EQUATIONS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 277-294
- Print publication:
- May 2015
-
- Article
- Export citation
Rectangular Lattice Boltzmann Equation for Gaseous Microscale Flow
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 306-330
- Print publication:
- April 2016
-
- Article
- Export citation
INVISCID AND VISCOUS MODELS OF AXISYMMETRIC FLUID JETS OR PLUMES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 3 / January 2012
- Published online by Cambridge University Press:
- 12 November 2012, pp. 228-250
-
- Article
-
- You have access
- Export citation
NUMERICAL SIMULATION OF MHD STAGNATION POINT FLOW TOWARDS A HEATED AXISYMMETRIC SURFACE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 3 / January 2011
- Published online by Cambridge University Press:
- 05 December 2011, pp. 301-308
-
- Article
-
- You have access
- Export citation
A NOTE ON THE NUMERICAL APPROACH FOR THE REACTION–DIFFUSION PROBLEM WITH A FREE BOUNDARY CONDITION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 3 / January 2010
- Published online by Cambridge University Press:
- 13 October 2010, pp. 317-330
-
- Article
-
- You have access
- Export citation
THE DEVELOPMENT AND STABILITY OF SOME NON-PLANAR BOUNDARY-LAYER FLOWS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 523-524
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
TEMPERATURE MODULATION IN RAYLEIGH–BÉNARD CONVECTION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 231-245
-
- Article
-
- You have access
- Export citation
A note on the separation of slow viscous flow near a sharp edge
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-244
- Print publication:
- December 1997
-
- Article
- Export citation
The stability of the Strokes layer in periodic orbital flow around a circular cylinder
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 225-238
- Print publication:
- December 1997
-
- Article
- Export citation
On the non-existence of periodic neutral-wave solutions to a complex-valued periodic differential equation
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 371-381
- Print publication:
- December 1996
-
- Article
- Export citation