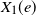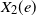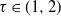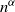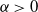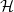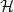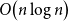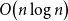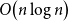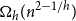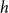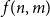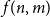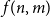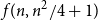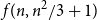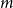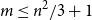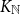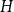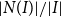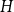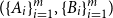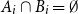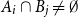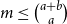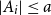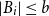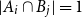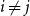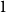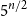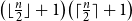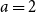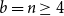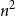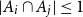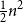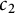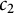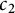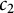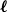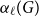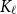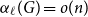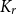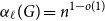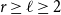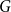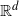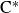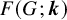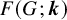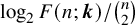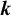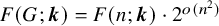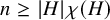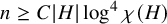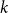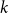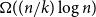Refine listing
Actions for selected content:
1007 results in 05Cxx
The winner takes it all but one
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 26 May 2023, pp. 137-152
- Print publication:
- March 2024
-
- Article
- Export citation
A pair degree condition for Hamiltonian cycles in 3-uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 17 May 2023, pp. 762-781
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Universal geometric graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 742-761
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal chordal subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 724-741
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramsey upper density of infinite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 703-723
-
- Article
- Export citation
Problems and results on 1-cross-intersecting set pair systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 691-702
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A result on the
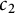 $c_2$ invariant for powers of primes
$c_2$ invariant for powers of primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1164-1178
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Clique-factors in graphs with sublinear
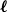 $\boldsymbol\ell$-independence number
$\boldsymbol\ell$-independence number
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 665-681
-
- Article
- Export citation
Expected number of faces in a random embedding of any graph is at most linear
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 682-690
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local limits of spatial inhomogeneous random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 April 2023, pp. 793-840
- Print publication:
- September 2023
-
- Article
- Export citation
Random amenable C*-algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 345-366
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Breaking of ensemble equivalence for dense random graphs under a single constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1181-1200
- Print publication:
- December 2023
-
- Article
- Export citation
Stability for the Erdős-Rothschild problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
Concordance of spatial graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 March 2023, pp. 1091-1108
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Degree distributions in recursive trees with fitnesses
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 March 2023, pp. 407-443
- Print publication:
- June 2023
-
- Article
- Export citation
Ramsey numbers of cycles versus general graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 February 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple random walks on graphs: mixing few to cover many
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 February 2023, pp. 594-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRAVERSING A GRAPH IN GENERAL POSITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. 353-365
- Print publication:
- December 2023
-
- Article
- Export citation
Random multi-hooking networks
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 13 February 2023, pp. 100-114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation