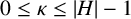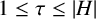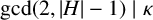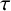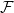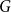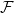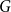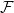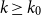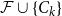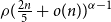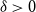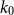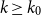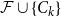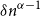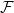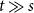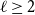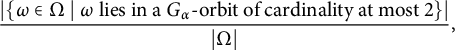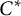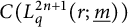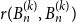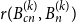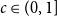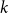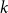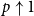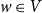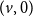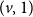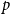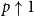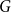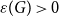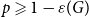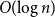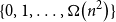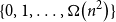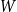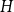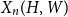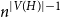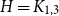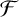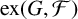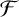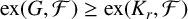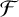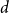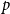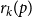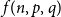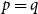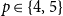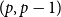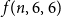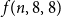Refine listing
Actions for selected content:
1007 results in 05Cxx
A NOTE ON REGULAR SETS IN CAYLEY GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 1-5
- Print publication:
- February 2024
-
- Article
- Export citation
Girth, magnitude homology and phase transition of diagonality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 221-247
- Print publication:
- February 2024
-
- Article
- Export citation
On Tournaments and negative dependence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 February 2023, pp. 945-954
- Print publication:
- September 2023
-
- Article
- Export citation
Bipartite-ness under smooth conditions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 546-558
-
- Article
- Export citation
Finite transitive groups having many suborbits of cardinality at most 2 and an application to the enumeration of Cayley graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 30 January 2023, pp. 345-366
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the classification and description of quantum lens spaces as graph algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 25 January 2023, pp. 246-282
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Battleship, tomography and quantum annealing
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 758-773
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SIZE, SPECTRAL RADIUS, DISTANCE SPECTRAL RADIUS AND FRACTIONAL MATCHINGS IN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 187-199
- Print publication:
- October 2023
-
- Article
- Export citation
Convergence of blanket times for sequences of random walks on critical random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 478-515
-
- Article
- Export citation
Off-diagonal book Ramsey numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 516-545
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A factor of i.i.d. with uniform marginals and infinite clusters spanned by equal labels
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 3707-3725
- Print publication:
- November 2023
-
- Article
- Export citation
The bunkbed conjecture holds in the
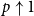 $p\uparrow 1$ limit
$p\uparrow 1$ limit
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 363-369
-
- Article
- Export citation
A bipartite version of the Erdős–McKay conjecture
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 465-477
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluctuations of subgraph counts in graphon based random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 428-464
-
- Article
- Export citation
LARGE
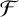 $\mathcal {F}$-FREE SUBGRAPHS IN
$\mathcal {F}$-FREE SUBGRAPHS IN 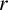 $r$-CHROMATIC GRAPHS
$r$-CHROMATIC GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 02 December 2022, pp. 200-204
- Print publication:
- October 2023
-
- Article
- Export citation
Supercritical site percolation on the hypercube: small components are small
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 422-427
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New upper bounds for the Erdős-Gyárfás problem on generalized Ramsey numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 349-362
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirac-type results for tilings and coverings in ordered graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 November 2022, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An elementary approach to component sizes in critical random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1228-1242
- Print publication:
- December 2022
-
- Article
- Export citation
Strong couplings for static locally tree-like random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1261-1285
- Print publication:
- December 2022
-
- Article
- Export citation