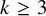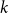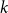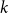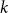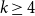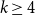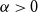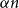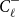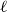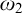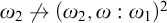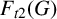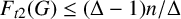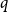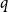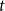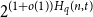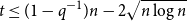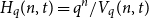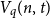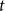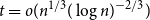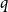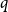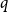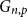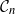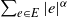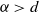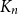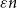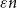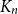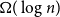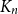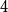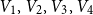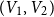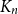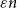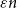Refine listing
Actions for selected content:
1007 results in 05Cxx
Disparity-persistence and the multistep friendship paradox
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 290-298
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Resolution of the Erdős–Sauer problem on regular subgraphs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the maximum number of edges in
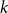 $k$-critical graphs
$k$-critical graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 24 July 2023, pp. 900-911
-
- Article
- Export citation
The codegree Turán density of tight cycles minus one edge
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 05 July 2023, pp. 881-884
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTABLE VS DESCRIPTIVE COMBINATORICS OF LOCAL PROBLEMS ON TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1835-1849
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weakly interacting oscillators on dense random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 June 2023, pp. 255-278
- Print publication:
- March 2024
-
- Article
- Export citation
COMPLETE BIPARTITE PARTITION RELATIONS IN COHEN EXTENSIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the size-Ramsey number of grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 874-880
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UPPER BOUNDS ON THE SEMITOTAL FORCING NUMBER OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 177-185
- Print publication:
- April 2024
-
- Article
- Export citation
On sparsity, power-law, and clustering properties of graphex processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 1211-1253
- Print publication:
- December 2023
-
- Article
- Export citation
Archaeology of random recursive dags and Cooper-Frieze random networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 13 June 2023, pp. 859-873
-
- Article
- Export citation
On the number of error correcting codes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 819-832
-
- Article
- Export citation
Spanning
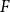 $F$-cycles in random graphs
$F$-cycles in random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 833-850
-
- Article
- Export citation
Unimodular random one-ended planar graphs are sofic
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 851-858
-
- Article
- Export citation
A smoother notion of spread hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 08 June 2023, pp. 809-818
-
- Article
- Export citation
On a wider class of prior distributions for graphical models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 08 June 2023, pp. 230-243
- Print publication:
- March 2024
-
- Article
- Export citation
Extrema of a multinomial assignment process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 06 June 2023, pp. 198-213
- Print publication:
- March 2024
-
- Article
- Export citation
Propagation of chaos and large deviations in mean-field models with jumps on block-structured networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1301-1361
- Print publication:
- December 2023
-
- Article
- Export citation
Upper large deviations for power-weighted edge lengths in spatial random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 34-70
- Print publication:
- March 2024
-
- Article
- Export citation
Unavoidable patterns in locally balanced colourings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 01 June 2023, pp. 796-808
-
- Article
- Export citation